Understanding the origin of cosmic acceleration presents a stunning opportunity for theorists. As discussed in Section 2, a smooth component with large negative pressure has repulsive gravity and can lead to the observed accelerated expansion within the context of GR. This serves to define dark energy. There is no shortage of ideas for what dark energy might be, from the quantum vacuum to a new, ultra-light scalar field. Alternatively, cosmic acceleration may arise from new gravitational physics, perhaps involving extra spatial dimensions. Here, we briefly review the theoretical landscape.
5.1.1. VACUUM ENERGY
Vacuum energy is simultaneously the most plausible and most puzzling
dark energy candidate. General covariance requires that the
stress-energy of the vacuum takes the form of a constant times
the metric tensor, TVACµ
= 
VAC
gµ.
Because the
diagonal terms (T00,
Tii) of the stress-energy tensor
Tµ are the energy density
and minus the pressure of the fluid, and
gµ is just the Kronecker
delta, the vacuum has a pressure equal to minus its energy density,
pVAC =
-VAC.
This also means that vacuum energy is mathematically
equivalent to a cosmological constant.
Attempts to compute the value of the vacuum energy density
lead to very large or divergent results. For each mode of a quantum field
there is a zero-point energy
/ 2, so that the energy
density of the quantum vacuum is given by
 |
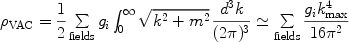(17) |
where gi accounts for the degrees of freedom of the field (the sign of gi is + for bosons and - for fermions), and the sum runs over all quantum fields (quarks, leptons, gauge fields, etc). Here kmax is an imposed momentum cutoff, because the sum diverges quartically.
To illustrate the magnitude of the problem, if the energy density
contributed by just one field is to be at most the critical density,
then the cutoff kmax must be <
0.01 eV — well below any energy scale where one could
have appealed to ignorance of physics beyond. [Pauli apparently carried
out this calculation in the 1930's, using the electron mass scale for
kmax and finding that the size of the Universe,
that is, H-1, "could not even reach to the
moon"
[Straumann 2002].]
Taking the cutoff to be the Planck scale
( 
1019 GeV), where one expects quantum field theory in a
classical spacetime metric to break down, the zero-point energy density
would exceed the critical density by some 120 orders-of-magnitude! It is
very unlikely that a classical contribution to the vacuum energy density
would cancel this quantum contribution to such high precision. This very
large discrepancy is known as the cosmological constant problem
[Weinberg 1989].
Supersymmetry, the hypothetical symmetry between bosons and fermions,
appears to provide only partial help. In a supersymmetric (SUSY) world,
every fermion in the standard model of particle physics has an
equal-mass SUSY bosonic partner and vice versa, so that fermionic and
bosonic zero-point contributions to
VAC
would
exactly cancel. However, SUSY is not a manifest symmetry in Nature: none
of the SUSY particles has yet been observed in collider experiments, so
they must be substantially heavier than their standard-model
partners. If SUSY is spontaneously broken at a mass scale M, one
expects the imperfect cancellations to generate a finite vacuum energy
density
VAC
~ M4. For the
currently favored value M ~ 1 TeV, this leads to a
discrepancy of 60 (as opposed to 120) orders of magnitude with
observations. Nonetheless, experiments at the Large Hadron Collider
(LHC) at CERN will soon begin searching for signs of SUSY, e.g., SUSY
partners of the quarks and leptons, and might shed light on the
vacuum-energy problem.
Another approach to the cosmological constant problem involves the idea
that the vacuum energy scale is a random variable that can take on
different values in different disconnected regions of the
Universe. Because a value much larger than that needed to explain the
observed cosmic acceleration would preclude the formation of galaxies
(assuming all other cosmological parameters are held fixed), we could
not find ourselves in a region with such large
VAC
[Weinberg 1987].
This anthropic
approach finds a possible home in the landscape version of string
theory, in which the number of different vacuum states is very large and
essentially all values of the cosmological constant are
possible. Provided that the Universe has such a multiverse structure,
this might provide an explanation for the smallness of the cosmological
constant
[Bousso
& Polchinski 2000,
Susskind 2003].
 |
Figure 10. Generic scalar potential
V( |
5.1.2. SCALAR FIELDS Vacuum energy
does not vary with space or time and is not dynamical. However,
by introducing a new degree of freedom, a scalar field
, one can make
vacuum energy effectively dynamical
[Ratra &
Peebles 1988,
Wetterich 1988,
Frieman et
al. 1995,
Zlatev, Wang &
Steinhardt 1992].
For a scalar field , with
Lagrangian density
= 1/2
µ
µ
-
V( ), the
stress-energy takes the form of a perfect fluid, with
 |
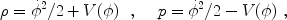(18) |
where is assumed to be
spatially homogeneous, i.e.,
(
, t) =
(t),
2/2 is the
kinetic energy, and
V( ) is the
potential energy; see Fig. 10. The evolution of
the field is governed by its equation of motion,
 |
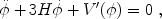(19) |
where a prime denotes differentiation with respect to
.
Scalar-field dark energy can be described by the equation-of-state parameter
 |
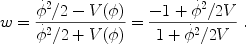(20) |
If the scalar field evolves slowly,
2 / 2V
<< 1, then w
-1, and the scalar
field behaves like a slowly varying vacuum energy, with
VAC(t)
V[ (t)].
In general, from Eq. (20), w can take on
any value between -1 (rolling very slowly) and +1 (evolving very
rapidly) and varies with time.
Many scalar field models can be classified dynamically as
"thawing" or "freezing"
[Caldwell
& Linder 2005].
In freezing models, the field rolls more slowly as
time progresses, i.e., the slope of the potential drops more rapidly
than the Hubble friction term
3H in
Eq. (19). This can happen if, e.g.,
V() falls off
exponentially or as an inverse power-law at
large . For thawing models,
at early times the field is frozen by
the friction term, and it acts as vacuum energy; when the expansion rate
drops below H2 =
V''(), the field begins
to roll and w evolves away from -1. The simplest example
of a thawing model is a scalar field of mass
m, with
V() =
m2
2/2.
Since thawing and freezing fields tend to have different trajectories of
w(z), precise cosmological measurements might be able to
discriminate between them.
5.1.3. COSMIC COINCIDENCE AND SCALAR FIELDS
As Fig. 1 shows, through most of
the history of the Universe,
dark matter or radiation dominated dark energy by many orders of magnitude.
We happen to live around the time that dark energy has become important. Is
this coincidence between
DE
and
M an
important clue to
understanding cosmic acceleration or just a natural consequence of the
different scalings of cosmic energy densities and the longevity of the
Universe? In some freezing models, the scalar field energy density
tracks that
of the dominant component (radiation or matter) at early times and then
dominates at late times, providing a dynamical origin for the coincidence.
In thawing models, the coincidence is indeed
transitory and just reflects the mass scale of the scalar field.
5.1.4. MORE COMPLICATED SCALAR-FIELD MODELS
While the choice of the potential
V() allows a large
range of dynamical
behaviors, theorists have also considered the implications of modifying the
canonical form of the kinetic energy term 1/2
µ
µ
in the Lagrangian. By
changing the sign of this term, from Eq. 20 it is possible to have
w < -1
[Caldwell
2002],
although such theories are typically unstable
[Carroll, Hoffman
& Trodden 2003].
In "k-essence," one introduces a field-dependent kinetic term
in the Lagrangian to address the coincidence problem
[Armendariz-Picon, Mukhanov & Steinhardt 2000].
5.1.5. SCALAR-FIELD ISSUES Scalar-field models raise new questions and possibilities. For example, is cosmic acceleration related to inflation? After all, both involve accelerated expansion and can be explained by scalar field dynamics. Is dark energy related to dark matter or neutrino mass? No firm or compelling connections have been made to either, although the possibilities are intriguing. Unlike vacuum energy, which must be spatially uniform, scalar-field dark energy can clump, providing a possible new observational feature, but in most cases is only expected to do so on the largest observable scales today (see Section 10.2.1).
Introducing a new dynamical degree of freedom allows for a richer variety of
explanations for cosmic acceleration, but it is not a panacea. Scalar field
models do not address the cosmological constant problem: they simply assume
that the minimum value of
V() is very small or
zero; see Fig. 10.
Cosmic acceleration is then attributable to the fact that the Universe
has not yet reached its true vacuum state, for dynamical reasons.
These models also pose new
challenges: in order to roll slowly enough to produce accelerated expansion,
the effective mass of the scalar field must be very light compared to other
mass scales in particle physics,
m
(V''())1/2
3H0
10-42 GeV,
even though the field amplitude is typically of order
the Planck scale, ~
1019 GeV. This hierarchy,
m
/ ~
10-60, means that the scalar field potential must be
extremely flat. Moreover, in order not to spoil this flatness, the
interaction strength of the field with itself must be extremely weak, at
most of order 10-120 in
dimensionless units; its coupling to matter must also be very weak to be
consistent with constraints upon new long-range forces
[Carroll
1998].
Understanding such very small numbers and ratios makes
it challenging to connect scalar field dark energy with particle physics
models
[Frieman et
al. 1995].
In constructing theories that go beyond the standard model of particle
physics, including those that incorporate primordial inflation,
model-builders
have been strongly guided by the requirement that any small dimensionless
numbers in the theory should be protected by symmetries from large quantum
corrections (as in the SUSY example above). Thus far, such model-building
discipline has not been the rule among cosmologists working on dark energy
models.
A very different approach holds that cosmic acceleration is a manifestation of new gravitational physics rather than dark energy, i.e., that it involves a modification of the geometric as opposed to the stress-tensor side of the Einstein equations. Assuming that 4-d spacetime can still be described by a metric, the operational changes are twofold: (1) a new version of the Friedmann equation governing the evolution of a(t); (2) modifications to the equations that govern the growth of the density perturbations that evolve into large-scale structure. A number of ideas have been explored along these lines, from models motivated by higher-dimensional theories and string theory [Dvali, Gabadadze & Porrati 2000, Deffayet 2001] to phenomenological modifications of the Einstein-Hilbert Lagrangian of GR [Carroll et al. 2004, Song, Hu & Sawicki 2007].
Changes to the Friedmann equation are easier to derive, discuss, and analyze. In order not to spoil the success of the standard cosmology at early times (from big bang nucleosynthesis to the CMB anisotropy to the formation of structure), the Friedmann equation must reduce to the GR form for z ≫ 1. As a specific example, consider the model of [Dvali, Gabadadze & Porrati2000], which arises from a five-dimensional gravity theory and has a 4-d Friedmann equation,
 |
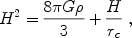(21) |
where rc is a length scale related to the
5-dimensional gravitational constant. As the energy density in matter
and radiation, ,
becomes small, there is an accelerating solution,
with H = 1 / rc. From the viewpoint of
expansion, the additional term in the Friedmann equation has the same
effect as dark energy that has an equation-of-state parameter which
evolves from w = -1/2 (for z ≫ 1) to w =
-1 in the distant future. While attractive, it is not clear that
a consistent model with this dynamical behavior exists (e.g.,
[Gregory et
al. 2007]).
Instead of modifying the right or left side of the Einstein equations to explain the supernova observations, a third logical possibility is to drop the assumption that the Universe is spatially homogeneous on large scales. It has been argued that the non-linear gravitational effects of spatial density perturbations, when averaged over large scales, could yield a distance-redshift relation in our observable patch of the Universe that is very similar to that for an accelerating, homogeneous Universe [Kolb, Matarrese & Riotto 2006], obviating the need for either dark energy or modified gravity. While there has been debate about the amplitude of these effects, this idea has helped spark renewed interest in a class of exact, inhomogeneous cosmologies. For such Lemaître-Tolman-Bondi models to be consistent with the SN data and not conflict with the isotropy of the CMB, the Milky Way must be near the center of a very large-scale, nearly spherical, underdense region [Tomita 2001, Alnes, Amarzguioui & Gron 2006, Enqvist 2007]. Whether or not such models can be made consistent with the wealth of precision cosmological data remains to be seen; moreover, requiring our galaxy to occupy a privileged location, in violation of the spirit of the Copernican principle, is not yet theoretically well-motivated.
There is no compelling explanation for cosmic acceleration, but many intriguing ideas are being explored. Here is our assessment:
The ideas underlying many of these approaches, from attempting to explain the smallness of quantum vacuum energy to extending Einstein's theory, are bold. Solving the puzzle of cosmic acceleration thus has the potential to advance our understanding of many important problems in fundamental physics.