4. GROWTH AND EXPANSION

Within the theory of general relativity, the cosmic expansion history completely determines the growth of matter density perturbations on large scales. On smaller scales the state of the matter, e.g. the Jeans length defined by pressure effects, enters as well and when density fluctuations go nonlinear then radiative and gas heating and cooling, star formation, feedback etc. affect the formation and evolution of structure. Here we consider only the large scale, linear regime and the role that growth observations can play in mapping the cosmological expansion.

4.1. Growth of density perturbations

For a matter density perturbation , its evolution is reduced from the Newtonian exponential growth on the gravitational dynamical timescale t_dyn = 1 / (G )^1/2 to power law growth on a Hubble timescale by the drag induced from the cosmological expansion. Generally,

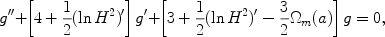(9)

where g = ( / ) / a is the normalized growth, a prime denotes differentiation with respect to lna, and the dimensionless matter density _m(a) = _m a^-3 / [H / H₀]². Thus the growth indeed depends only on the expansion history H (the matter density is implicit within the high redshift, matter dominated expansion behavior).

In a matter dominated epoch, the solution is / ~ a, so we defined g such that it would be constant (which we can arrange to be unity) in such a case. In an epoch dominated by an unclustered component with equation of state w, matter density perturbations do not grow. Note that this is due to the small source term, not the Hubble drag - indeed the Hubble drag term is proportional to 5-3w and is less strong in a radiation dominated universe than a matter dominated universe, yet matter density perturbations still do not grow in the radiation epoch. If one somehow fixed _m(a) as one changed w, then increasing w indeed aids growth. For domination by a component with w < 0 (not acceleration per se) there is the double whammy of reduced source term and increased friction.

As the universe makes the transition from being dominated by a w > 0 component to matter domination, the solution is

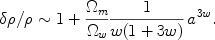(10)

One can see the transition from no growth ~ constant to growth (with ~ a for a radiation-matter transition). For a transition from matter domination to being dominated by a w < 0 component, to first order

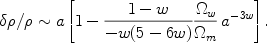(11)

Finally, for a w = 0 component that does not behave in the standard fashion, e.g. a constant fraction F of the matter density does not clump, then

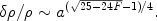(12)

For example, a small fraction _e of early dark energy with w = 0 leads to / ~ a^{1 - (3/5)_e} at early times. See [92, 93, 9] for early discussion of these growth behaviors in multicomponent universes.

Since the origin of the density perturbation source term is the Poisson equation, basically contributing 4G_N , any modification to this equation gives an effective F(k, a) ≡ [G _m(k, a)] / [G_{N m}(a)]_std that produces modified growth, where the wavenumber k allows for spatially dependent modifications. If F is nearly constant in time, then the growth is determined by Eq. (12). However, if the physical origin of the modification also affects the expansion, as from a time dependent gravitational coupling G_N, then one must alter the other growth equation terms as well to obtain the solution.

Growth measurements, being integrals from high redshift, can probe the high redshift universe. For example, a measurement of the growth factor at, say, z = 2 that agrees with a CDM model mapped out at lower redshift ensures that the high redshift epoch of matter domination occurred substantially as expected. Specifically, if the linear growth factor at z = 2 deviates by less than 5%, then for a monotonically varying dark energy model described by w(a) = w₀ + w_a(1 - a), we can limit w_a < 0.6 or w(z = 2) < -0.6. We can also constrain an intermediate, transient epoch of acceleration in the cosmic expansion. Growth measurements can place tight constraints on this mechanism for easing the coincidence problem [94], as shown in Figure 13. To prevent strong deviations in growth that would be evident in measurements, the period of such acceleration must be much shorter than the characteristic Hubble timescale (and hence apparently "unnatural").

Figure 13. Growth measurements can strongly constrain events in the cosmological expansion such as an intermediate epoch of acceleration. The left panel show the deviations from the CDM growth, in the present total growth g0 and growth ratio R = g(a = 0.35) / g0, for a transition to total equation of state -1 lasting a period ln a, ending at redshift zu. The right panel shows the limit on the length of the acceleration allowed as a function of transition redshift, in order for deviations to the total growth to be less than 10%.

Overall, the growth history has the potential to constrain the expansion history. However, there are some obstacles. The growth also depends on the initial conditions, couplings to other components, and deviations of gravity from general relativity. For example, in a radiation dominated universe growth should not occur, but if the perturbation evolution has some "velocity" from a previous matter dominated epoch it can proceed with a slow, lna growth. (Similarly, growth persists into an accelerating epoch.) Another example is that in the prerecombination universe baryons were tightly coupled to photons, preventing growth [95]. Finally, it is quite difficult to detect the matter perturbations per se, instead we observe light from galaxies - a biased tracer of the density field. Separating the absolute growth factor from the bias, or the relative growth from an evolution in bias, is nontrivial [96]. Weak gravitational lensing (see Section 4.3 below) offers a way around these issues.

Measurements of growth are presently not clean probes of the expansion history, especially since, as Eq. (9) indicates, precision knowledge of _m is required to truly use this approach to map H(z). Redshift distortion measurements of the growth of the matter velocity field (rather than density), employing d ln g / d ln a, have similar issues. See [97, 98] for good overviews of the current status of growth measurements.

4.2. Abundance tests

Under gravitational instability, mass aggregates and galaxies and clusters of galaxies form, evolving in number and mass. The abundance as a function of redshift of particular classes of objects will involve (among other variables) the initial power spectrum, astrophysical processes such as dissipation and feedback, and the expansion rate of the universe, as well as a robust observational proxy for mass. Two famous examples of using galaxy abundances as cosmological probes are in a 1975 paper "An Accelerating Universe" [99] and in 1986 "Measurement of the Mass Density of the Universe" [100]. As the titles suggest, the data led to opposite conclusions and each was quickly recognized to be showing more about astrophysical evolution of the objects than the cosmological expansion history.

New generations of experiments are underway to count sources as a function of redshift and mass, selecting samples through their detection in the Sunyaev-Zel'dovich effects, X-ray flux, optical flux, or weak gravitational lensing shear. Currently, data is insufficient to give robust cosmological constraints on the expansion history. Note that observations do not actually measure an abundance per comoving volume, dN(m) / dV, which would show how structures grow in mass while their (nonevolving) numbers should stay constant. Rather they see dN / dz which involves distances through an extra factor of dV / dz. Thus observed abundances do not give a pure growth probe but mix geometry and growth - both an advantage and disadvantage.

4.3. Gravitational lensing

The gravitational potentials of massive structures deflect, focus, and shear bundles of light rays from more distant sources. The particular shear pattern combines information from both the lensing mass and the "focal length" defined by the source and lens distances from the observer. To date, most such data provides leverage on a combination of the matter density _m and the rms amplitude of mass fluctuations ₈. A few surveys so far quote further cosmological constraints - on the dark energy parameters in combination with other data sets [101], or on the presence of growth [102, 103, 104, 105, 106].

A number of interesting concepts for using gravitational lensing to map the cosmological expansion exist, though practicality has yet to be demonstrated. Both the magnification or convergence fields and the shear field carry cosmological information. For use as a geometric probe, one must separate astrophysical or instrumental effects, deconvolve the lens gravitational potential model, and measure the redshifts or redshift distribution of the lenses and sources accurately. See [82, 83, 84] for discussion of weak lensing as a geometric probe. Similarly, lensing offers promise to probe the growth history. Lensing of the CMB, where the source redshift is known, is another interesting application [107]. See [108] for far more discussion of weak lensing and its many uses than given here.

4.4. Testing gravity

4.4.1. First steps     Although the focus of this article is on mapping the cosmological expansion, since the growth history depends on both the expansion and the laws of gravity one could consider using expansion plus growth measurements to test the gravitational framework. This is an exciting possibility that has recently received considerable attention in the literature (see, e.g., [109, 37, 110, 111] for early work), although current data cannot provide significant constraints.

In addition to comparing predictions of specific theories of gravity to data, one basic approach is parametrization of gravitational cosmological effects. While one could define cosmological parameters _m^gr, w₀^gr, w_a^gr, say, derived from fitting the growth history and contrast these with those derived from pure expansion measurements, one could also keep the physics of cosmic expansion expressed through the well-defined (effective) parameters _m, w₀, w_a and look for physical effects from gravity beyond Einstein relativity in separate, clearly interpretable gravitational parameters.

The gravitational growth index was designed specifically to preserve this distinction of physical phenomena [112]. Here the matter density linear growth factor g = ( / ) / a is written

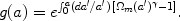(13)

See [112, 113, 114] for discussion of the accuracy, robustness, and basis of this form. However, gravity does more than affect the growth: it affects the light deflection law in lensing and the relation between the matter density and velocity fields. Since two potentials enter generically, in the time-time and space-space terms of the metric, [115, 116, 117, 118, 119, 120, 121, 122] and others have proposed two or more parameters for testing extensions to general relativity (GR). These may involve the ratio of metric potentials (unity for GR), as a cosmological generalization of the parametrized post-Newtonian quantity, and their difference (zero for GR), related to the anisotropic stress.

4.4.2. Problems parametrizing beyond-Einstein gravity     The two gravitational parameter approach is an exciting idea that deserves active exploration. Here, however, to balance the literature we undertake a more critical overview of this program. Difficulties to overcome include:

1. Reduction of two functions to two (or a small number) of parameters;

2. Spatial dependence, e.g. strong coupling or Vainshtein scales, or quantities living in real space vs. Fourier space;

3. Covariance among deviations in gravitational coupling, metric potentials, and fluid anisotropic stress.

We give very brief assessments of each item. For the first point, a successful proof of concept is the gravitational growth index, which for a wide class of theories adds a single (constant) parameter to describing linear growth. [114] explains why this works under certain conditions, basically requiring small deviations from standard cosmological expansion and gravity. Many theories indeed have small deviations, but these are often so small they become problematic to detect; other theories with larger deviations are either ruled out by, e.g., solar system tests or have scale dependence requiring multiple parameters.

Regarding the second point, in the parametrized post-Newtonian (PPN) formalism the ratio of metric potentials is defined in real space, e.g. (r) / (r). This is not equivalent to defining a parameter = _k / _k in Fourier space. Given some function f(r) = (r) + (r), it is not generically true that a nonlinear function F(f(r)) depends in the same manner on and . Thus many power spectra, e.g. involving <( + )²> for the integrated Sachs-Wolfe effect, will not follow the simple formalism.

Spatial variation also does not preserve the functional dependence; for example, while the light deflection angle depends on the specific combination (r) + (r), the actual deflection at impact parameter b is not a function only of (b) + (b). Consider lensing in DGP [123] gravity, where

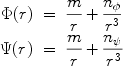(14) (15)

where the n's are related to extradimensional quantities. (Many IR modifications of gravity have this form, but note it is very different from the Yukawa form so general parametrization of spatial dependence may be difficult). Thus f(r) takes the form 2m / r + n / r³ and some function, say,

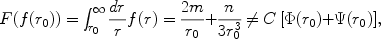(16)

for any constant C. More concretely, for deflection of light at impact parameter b from a point mass (extending [124]), we find the deflection angle

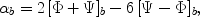(17)

breaking the functional form + with an extra term looking like a spurious anisotropic stress. Thus observations of lensing deflection do not tell us about a simple parameter in the form (1 + ), as we might hope.

Another issue concerns interdependence among different aspects of gravitational modifications. Variation in gravitational coupling may well occur alongside anisotropic stress, as in scalar-tensor theories. In Poisson's equation, therefore, one cannot define a Fourier space mass power spectrum <_k²> because the physical source involves <(G_{eff k})²> and it may not be clear how the interaction of these two quantities affects the result. This is reminiscent of varying constant theories where one can calculate the effects of a varying fine structure constant, say, but does not have a unified framework for understanding how the electron-proton mass ratio, say, varies simultaneously, and hence affects observations as well [125]. Confusion also arises between gravitational modifications and fluid microphysics, e.g. anisotropic stress of a component, coupling between components, or finite sound speed (see, e.g., [126]).

4.4.3. Levels of discovery     In summary, there is a rich array of challenges for a program seeking to parameterize beyond Einstein gravity. One ray of hope is that different observations depend differently on the quantities, some of which are outlined in Table 2 (also see [120]). In the theory realm, SN serve as pure geometric probes of the cosmological expansion, immune to the uncertainties imposed by these additional parameters (even G(t), see e.g. [131]), providing the most unambiguous understanding. This point is worth considering: all other methods in use rely on understanding the rest of the dark sector - dark matter and gravity - as they seek to explore dark energy. As well though, we should keep in mind the insight by Richard Feynman:

"Yesterday's sensation is today's calibration, and tomorrow's background."

Mapping the cosmological expansion with a simple, robust, and geometric method like supernovae provides a firm foundation as we also must probe deeper, with techniques that have more complex - richer - dependence on further variables revealing the microphysics and testing gravity. Mutual support among methods will be key to yielding understanding.

Table 2. Theory systematics occur even for some geometric probes, the cleanest astrophysically. For example, light deflection depends on the metric potentials as + , plus separating out the mass model, and baryon acoustic oscillations are sensitive to the validity of the usual CDM growth, hence affected by and (see, for example, [127] for difficulties in the braneworld case), new density perturbations due to the sound speed c_s (see, e.g., [128]) and anisotropic stress _s, variation of the gravitational coupling G with scale and time, and altered fluctuations due to matter coupling (see, e.g., [129, 130]).

Probe	Theory Systematic (dominant)	Theory Systematic (potential)
SN Ia	—	—
WL	+	cs, s, G(k,t)
BAO	, , cs,	s, G(k,t)