The main uncertainty in our future ability to map the cosmological
expansion is the level of control of systematics we can achieve.
In a reductio ad absurdum we can say that since one supernova explodes
every second in the universe we might measure 107 per year,
giving distance accuracies of 10% / (107)1/2 =
0.003% in ten redshift
slices over a ten year survey; or counting every acoustic mode in
the universe per redshift slice spanning the acoustic scale
determines the power spectrum to
3 /
(H-2 )
= (1/30)2
or 0.1%; or measuring weak lensing shear across the full sky with
0.1" resolution takes individual 1% shears to the 0.0003% level.
Statistics is not the issue: understanding of systematics is.
However it is much easier to predict the future of statistical measurements than systematic uncertainties. It is difficult to estimate what the future prospects really are. Large surveys are being planned assuming that uncertainties will be solved - or if the data cannot be used for accurately mapping the cosmic expansion it will still prove a cornucopia to many fields of astrophysics. Moreover, an abundance of surveys mentioned in the literature are various levels of vaporware: many have never passed a national peer review or been awarded substantial development funding or had their costs reliably determined. Rather than our listing such possibilities, the reader can peruse national panel reports such as the ESA Cosmic Vision program [158], US National Academy of Sciences' Beyond Einstein Program Assessment Committee report [159], or the upcoming US Decadal Survey of Astronomy and Astrophysics [160].
The current situation regarding treatment of systematics is mixed. In supernova cosmology, rigorous identification and analysis of systematics and their effects on parameter estimation is (almost) standard procedure. In weak lensing there exists the Shear Testing Programme [161], producing and analyzing community data challenges. Other techniques have less organized systematics analysis, where it exists, and the crucial rigorous comparison of independent data sets (as in [44]) is rare. Control methods such as blind analysis are also rare. We cannot yet say where the reality will lie between the unbridled statistical optimism alluded to in the opening of this section and current, quite modest measurements. Future prospects may be bright but considerable effort is still required to realize them.
Since prediction of systematics control is difficult, let us turn instead to intrinsic limits on our ability to map the expansion history - limits that are innate to cosmological observables. The expansion history a(t), like distances, is an integral over H = d ln a / dt, and does not respond instantaneously to the evolution of energy density (which in turn is an integral over the equation of state). As seen in Figures 7 - 8, the cosmological kernel for the observables is broad - no fine toothed comb exists for studying the expansion. This holds even where models have rapid time variation w' > 1, as in the e-fold transition model, or when considering principal components (see [162, 133] for illustrations).
(This resolution limit
on mapping the expansion is not unique to distances - the growth factor
is also an integral measure and the broad kernel of techniques like weak
lensing is well known. The Hubble parameter determined through BAO, say,
requires a redshift shell thickness
z
0.2 to obtain
sufficient
wave modes for good precision, limiting the mapping resolution.)
Thus, due to the innate cosmological dependences of observables, plus
additional effects such as Nyquist and statistics limits of wavemodes in
a redshift interval and coherence of systematics over redshift
[162],
we cannot expect mapping of the cosmological expansion with
finer resolution than
z
0.2 from next
generation data.
6.3. Limits on cosmic doomsday
Finally, we turn from the expansion history to the expansion future. As pointed out in Section 2.5, to determine the fate of our universe we must not only map the past expansion but understand the nature of the acceleration before we can know the universe's destiny - eternal acceleration, fading of dark energy, or recollapse.
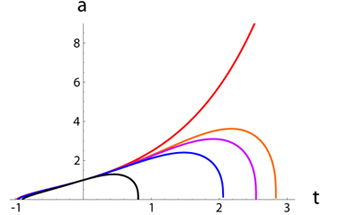
We do not yet have that understanding, but suppose we assume that the linear potential model of dark energy [38], perhaps the simplest alternative to a cosmological constant, is correct. Then we can estimate the time remaining before the fate of recollapse: the limit on cosmic doomsday. The linear potential model effectively has a single equation of state parameter and is well approximated by the family with wa = -1.5(1 + w0) when w0 is not too far from -1. Curves of the expansion history (and future) are illustrated in the left panel of Figure 19; the doomsday time from the present is given by
 |
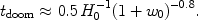(24) |
The current best constraints from data (cf. [163] for future limits) appear in the right panel of Figure 19, corresponding to tdoom > 24 Gy at 68% confidence level. It is obviously of interest to us to know whether the universe will collapse and how long until it does, so accurate determination of wa is important! The difference between doomsday in only two Hubble times from now and in three (a whole extra Hubble time!) is only a difference of 0.12 in wa.
 |
 |
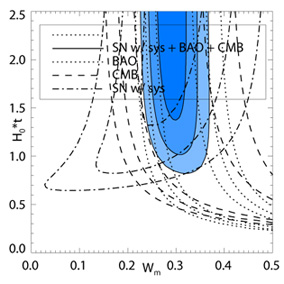Figure 19. The future expansion history in the linear potential model has a recollapse, or cosmic doomsday. Left panel: Precision measurements of the past history are required to distinguish the future fate, with the five curves corresponding to five values for the potential slope (the uppermost curve is for a flat potential, i.e. a cosmological constant). From [163]. Right panel: Current data constraints estimate cosmic doomsday will occur no sooner than ~ 1.5 Hubble times from now. From [164]. |
|