


Testing the effect of sub-grid models in galaxy formation simulations is best done not in cosmological simulations but in high-resolution numerical realizations of isolated galaxies 93, 46 (see section 2). These models are constructed on purpose to resemble observed galaxies, with a disk of gas and stars, eventually a stellar bulge, and always an extended, massive dark matter halo with structural properties (mass, spin, density profile) consistent with the results of cosmological simulations describing the hierarchical growth of CDM halos. The various components are in dynamical equilibrium, representing a stationary solution of the relevant dynamical equations for collisionless and fluid matter. Small deviations from equilibrium are present as a result of discretization and other approximations introduced by the numerical methods 93. These models by-pass all the issues of ab-initio galaxy formation and are built on the assumption of angular momentum conservation during the baryonic collapse.
Tests of the blast-wave feedback model 86 using such equilibrium galaxy models show that after a while the star formation rate and phase diagram of the galaxy become nearly steady-state (self-regulation). Locally, however, the phases are not in pressure equilibrium and a patchy, filamentary structure with bubbles arises that is well resemblant of observed galaxies (Figure 11). Other important properties of observed galaxies, such as the volumetric ratio between cold and hot gas, the thickness of the gaseous disk and the ratio between ordered, rotational motions and random motions in the stellar component, are also satisfactorily reproduced 86.
These idealized numerical experiments are useful for validating the phenomenological recipe contained in a given sub-grid model. Nonetheless, they give limited information on what happens in a realistic cosmological setting in which galaxies are always out of equilibrium as a result of mass accretion from their surroundings and frequent merging events with other galaxies.
An intermediate level of realism between equilibrium galaxy models and a
fully cosmological simulation is represented by models that follow the
formation of a single galaxy from
the cooling and collapse of gas within an isolated dark matter
halo. These models are more realistic because they do not start from an
idealized equilibrium condition and because they do follow the
assembly of the galaxy. However they differ from cosmological simulations
because they neglect the external tidal field and the merging with other
halos/galaxies during the galaxy assembly process
48,
50.
One fixes the specific angular momentum of the gas by choosing a value
of the spin parameter. Once the spin parameter is fixed, for example to
the mean value found for dark halos in cosmological simulations,
 ~ 0.035,
the baryonic mass fraction, namely
gas mass initially present in the dark halo, will control the properties
of the galaxy that will emerge from the collapse.
If the baryonic mass fraction fb (fb
= Mbaryon / Mvir, where
Mbaryon is the mass of baryons
in the halo and Mvir the total halo (virial) mass,
i.e. dark matter + baryons) is fairly high, comparable to the universal
baryon fraction expected in the standard LCDM cosmology
(fb ~ 0.17), a massive disk forms and undergoes soon a bar
instability, this being a common outcome of gravitational instability in
a rotating gaseous or stellar disk. As we mentioned in
section 2.4, the bar transfers angular
momentum outward and mass inward, leading to a steep
stellar density profile in the center and a much shallower profile in
the outer part. When a standard star formation recipe is included in the
simulation the bar becomes mostly stellar
because gas is efficiently converted into stars, and undergoes another
form of gravitational instability in the
vertical direction, known as "buckling instability"
94.
The latter instability deflects the orbits of stars away from the disk
plane, turning the elongated bar into a
roundish, bulge-like component. The latter is widely recognized as an
important mechanism of bulge formation, alternative to mergers between
galaxies
95,
96,
54.
After the buckling instability the simulated
galaxy looks like our Milky Way or the Andromeda galaxy, with a bulge
surrounded by a more massive and extended disk of stars and gas
48
(Figure 4).
~ 0.035,
the baryonic mass fraction, namely
gas mass initially present in the dark halo, will control the properties
of the galaxy that will emerge from the collapse.
If the baryonic mass fraction fb (fb
= Mbaryon / Mvir, where
Mbaryon is the mass of baryons
in the halo and Mvir the total halo (virial) mass,
i.e. dark matter + baryons) is fairly high, comparable to the universal
baryon fraction expected in the standard LCDM cosmology
(fb ~ 0.17), a massive disk forms and undergoes soon a bar
instability, this being a common outcome of gravitational instability in
a rotating gaseous or stellar disk. As we mentioned in
section 2.4, the bar transfers angular
momentum outward and mass inward, leading to a steep
stellar density profile in the center and a much shallower profile in
the outer part. When a standard star formation recipe is included in the
simulation the bar becomes mostly stellar
because gas is efficiently converted into stars, and undergoes another
form of gravitational instability in the
vertical direction, known as "buckling instability"
94.
The latter instability deflects the orbits of stars away from the disk
plane, turning the elongated bar into a
roundish, bulge-like component. The latter is widely recognized as an
important mechanism of bulge formation, alternative to mergers between
galaxies
95,
96,
54.
After the buckling instability the simulated
galaxy looks like our Milky Way or the Andromeda galaxy, with a bulge
surrounded by a more massive and extended disk of stars and gas
48
(Figure 4).
If the fraction of baryonic material is chosen low enough it is possible to reproduce a disk galaxy without a bulge component. The bar does not form, and thus no spheroid is produced, because this time the disk has a lower mass and can hardly become gravitationally unstable. The final galaxy looks similar to our neighbor bulgeless galaxy M33 (Figure 12).
 |
 |
 |
Figure 12. Top and middle panel: snapshots of a high-resolution galaxy formation simulation in an isolated halo that produce a bulgeless galaxy thanks to a low baryon fraction 48, 130 (2006, 2007 Blackwell Publishing Ltd). See section 4 for details. The top panel shows a region of 60 kpc on a side in which the cold clouds produced by thermal instability in the infalling gas are visible. The middle panel zooms in the inner 20 kpc, showing the disk-dominated galaxy with flocculent spiral arms that resembles the bulgeless nearby M33 galaxy. Bottom: the nearby bulgeless galaxy M33. |
The origin of exponential stellar density profiles The M33-like galaxy emerging from the simulation with a low baryon fraction does not exhibit an exponential stellar surface density profile such as that of typical bulgeless galaxies, rather it shows a sharp upturn within a few hundred parsecs from the center. Indeed, this upturn is caused by a dense clump of gas and stars, containing of order 109 solar masses. Central stellar concentrations of comparable masses, known as stellar nuclei, are seen in some bulgeless galaxies but their typical sizes are ten times smaller, so that they do not affect the surface density profile at scales of hundreds of parsecs 97. Moreover, a large fraction of bulgeless galaxies does not have such nuclei and shows a stellar exponential profile across several kiloparsecs in radius. This is currently one of the most important problems of disk formation. The location of a parcel of gas in the disk after the collapse, namely how close to the center such a parcel settles into centrifugal equilibrium, determines the gas density profile, which in turn sets the stellar density profile via the conversion of gas into stars. Such location is determined by the combined action of gravity, pressure and rotational support. The presence of a dense concentration in the simulations might suggest a "second" angular momentum problem at small scales. It is a second problem because it occurs even when the total spurious angular momentum loss in the disk is down to a few percent thanks to high resolution 48. As we mentioned in section 2, numerical loss of angular momentum near the center of the potential is hard to tackle even at high resolution, and might be playing a role in this case. However, this cannot be the only issue. In fact, one dimensional spherical numerical models of gas collapse in cuspy CDM halos that impose angular momentum conservation also predict that same inner upturn of the stellar density profile 10. This seems to be a result of how the gas settles in centrifugal equilibrium in the cuspy potential of a CDM halo 10, 13. The upturn in the profile is caused by the collapse of the innermost shells of the gas distribution, and these are the ones that collapse first because they have the shortest free-fall time.
One possibility to reconcile the simulations with the observations would be to alter the halo potential - if the halo has finite density core its potential well would be shallower and the gas would likely satisfy the the centrifugal equilibrium condition further out from the center, avoiding the formation of the dense central clump. This of course would require to invoke some mechanism that modifies the halo profiles predicted by the CDM simulations, or even to resort to an alternative cosmological model. Both options should not be disregarded but one may wonder whether such a drastic change of scenario is really required. Since pressure also plays a role in deciding the radius at which gas comes into centrifugal equilibrium, as well as its distance above and below the plane, hence ultimately its mass distribution, the answer could lie in the details of gas thermodynamics during disk assembly.
Here we present preliminary results suggesting that the model assumed for energy feedback in the disk has a big impact on the slope of the stellar density profile. We recomputed the same disk formation models presented in already published work 48 using the blast-wave feedback model (40% of the energy of the supernovae explosions is damped to the gas in this particular simulation). The gas disk has an irregular and flocculent structure without a significant central concentration, at odds with the simulation without feedback (Figure 13). The stellar disk has a lower average density and its surface density profile has a much flatter slope compared to the case without feedback (Figure 14) and shows a milder upturn at small scales; what is most important, however, is that such upturn appears only after a couple of Gyrs of evolution. Therefore it is related to the internal evolution of the disk (spurious and/or physical) rather than being caused by the initial conditions (i.e. by gas collapse in a cuspy halo profile).
 |
Figure 13. Comparison of disk galaxy (isolated collapse simulation) with thermalfeedback 48 (left, a temperature floor is used - see text) and blast-wave feedback 86 (right). The gaseous disk is shown on top and the stellar disk is shown at the bottom. Boxes are 20 kpc on a side, the galaxy halo has Vc = 70 km/s before collapse, simulations have 5 × 105 SPH particles and 106 dark matter particles and are shown after about 1 Gyr. |
A single exponential curve can reproduce the slope of most of the stellar mass distribution, which clearly was not the case with thermal feedback (see Figure 14). So now the problem has shifted from forming a pure exponential profile to preserving it for a timescale long enough, i.e. many Gyrs, to explain why we observe many pure exponential disks in the local Universe. The fact that the stellar profile becomes closer to exponential with using blast-wave feedback is not trivially related to the higher pressure support in the gas disk produced by the supernovae explosions. Indeed the simulations that we previously published 48 included a minimum temperature below which the gas was not allowed to cool in order to crudely mimic the heating due to feedback. Such temperature floor was comparable to the mean temperature of the gas in the blast-wave feedback simulation (30000-50000 K). After all, the models with a temperature floor can explain observed trends of increasing thickness of the disk, lowered star formation efficiency and higher gas fractions in the disk with decreasing galaxy mass due to the enhanced pressure support 98.
However, while the temperature floor is by construction the same everywhere in the disk, the blast-wave feedback produces a two-phase medium such that density, pressure and temperature can have significant local variations (see previous section). Indeed the morphological appearances of the two disks are very different (see Figure 13), with the blast-wave model producing a much more flocculent and irregular gas disk which resembles more closely that of late-type low mass galaxies such as the nearby Large Magellanic Cloud 86. The bubbles produced by supernovae literally punch holes in the disk and push the neighboring cold gas squeezing it into dense filaments, where star formation can go on. The fact that the cold gas is confined to filaments and cannot fill a large volume naturally avoids the formation of large dense clumps of gas, possibly explaining why the blast-wave feedback is more effective at suppressing the upturn of the surface density profile compared to a model with a uniform temperature floor.
Cosmological simulations adopting the model of the effective equation of state 87, 91 were also able to produce a disk galaxy having a nearly exponential profile without a central dense clump 56 but the stellar disk was too thick and was rotating too slowly in the central few kiloparsecs compared to typical disk-dominated galaxies - the inner disk was deficient in specific angular momentum by a factor of 2. This suggests that the pressurization of the interstellar medium produced by this model, which determines the vertical structure of the disk, might be excessive and might disfavour the formation of a realistic thin disk. These results reinforce the idea that the solution of the exponential disk profiles lies in a correct model of the thermodynamics of the interstellar medium and star formation rather than in drastic modifications of the underlying cosmological model.
4.2. Cosmological simulations of disk formation with blast-wave feedback
When applied to galaxies of a range of masses forming in a cosmological simulation the blast-wave feedback model allows to improve significantly the match with real galaxies in at least three ways compared to the case in which a simple thermal feedback model is used 55, 100:
(1) At a given resolution it produces more extended disks with a smaller bulge (although increasing the mass resolution has the strongest effect in reducing the bulge-to-disk mass ratio), in line with what was found for isolated collapse experiments (Figure 9).
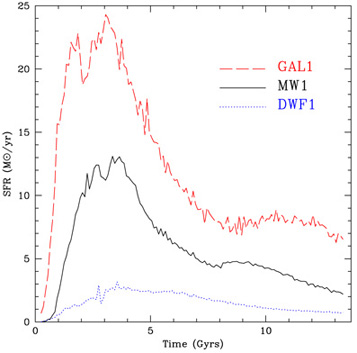
(2) It produces automatically the right trend of star formation histories with galaxy mass (Figure 15).
(3) It produces galaxies that lie close to the observed correlation between rotational velocity of the disk and luminosity of the galaxy, also known as Tully-Fisher relation 99.
(4) it allows to predict correctly the stellar mass -metallicity relation 100 measured in local galaxies 101 and at z = 2 102, according to which more massive galaxies are also more metal rich (Figure 15).
 |
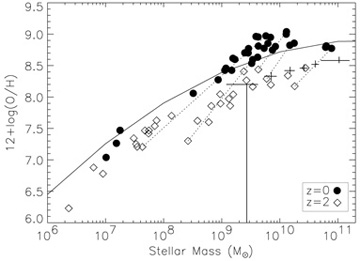 |
Figure 15. Top:Star formation histories of simulated galaxies of varying mass in high-res cosmological simulations 55 (2007 Blackwell Publishing Ltd). The three galaxies have the following masses within the virial radius;1.6 × 1011 solar masses (DWF1), 1.15 × 1012 solar masses (MW1) and 3.1 × 1012 solar masses (GAL1). Bottom: Mass-metallicity relation for simulated galaxies at z = 0 (filled circles) and z = 2 (open diamonds) 100 (reproduced by permission of the AAS, 2007). The solid curved line is the observational fit to > 53,000 galaxies in the Sloan Digital Sky Survey 101, shifted down by -0.26 dex as found in the observations 102. Error bars show the observational mass-metallicity relation at z = 2 102. Dotted lines connect some of the z = 0 galaxies to their progenitors at z = 2 , showing how galaxies evolve in the plane with time. |
The Tully-Fisher relation is directly connected with the most important aspects of galaxy formation 103, 104. namely the amount of gas which forms stars and thus determines the luminosity of the galaxy, and the depth of the gravitational potential well, which determines the magnitude of rotation. In the past numerical simulations have failed to reproduce this relation. Not surprisingly, the only other work in which simulated galaxies were falling close to the observed Tully-Fisher is the same work in which an exponential, disk-dominated galaxy was obtained 56. In the latter work the authors also obtained a nearly flat rotation curve for one of their simulated galaxies thanks to the absence of a dense and massive bulge. This single rotation curve was flatter than that of the galaxies in 55, although a new series of blast-wave feedback simulations, which consider a larger variety of initial conditions, also includes some objects with nearly flat rotation curves (Governato et al., in preparation). A flat rotation curve with a very small bulge component is also obtained in recent AMR simulations that, thanks to a resolution better than 50 pc, are able to follow directly the dynamics and thermodynamics of bubbles produced by supernovae explosions, although the calculation is carried out only until z = 3 43.
Regarding the third point, the trend between star formation history and galaxy mass is such that lower mass galaxies have progressively more extended star formation histories, namely a larger fraction of their stars forms at progressively later epochs. This is the observed "downsizing" of galaxies, namely the fact that smaller galaxies appear to have formed more recently 105. Taken at face value, for years downsizing has been considered as a fundamental problem of the cold dark matter model, which predicts that structure formation proceeds from small to large halos in a bottom-up fashion. The blast-wave feedback model has allowed to resolve this discrepancy by decoupling the evolutionary timescale of the baryonic component from that of the dark matter component owing to their different energetics; in low mass galaxies gas is less gravitationally bound to the halos and can thus be more dramatically affected by the heating due to supernovae explosions 106, with the result that star formation is quenched and more gas is available at later epochs to keep forming stars. In other words, the star formation in small galaxies is diluted over a much longer time span, so that when their light is measured they appear young today despite the fact that their halos assembled early. Dilution also means a lower average star formation rate relative to large galaxies (Figure 15). another well established observational distinction between low mass and high mass galaxies.
A lower average star formation rate also implies that at the current epoch low mass galaxies should be more gas rich relative to high mass galaxies. This happens in the simulations 55 and is in agreement with the observed trend of increasing gas fraction towards decreasing galaxy mass 107. The gas fractions in the blast-wave feedback runs are actually significantly higher than in models that use a purely thermal feedback.
Realistic gas fractions and star formation rates are also obtained with simulations employing the effective equation of state 56. Unfortunately, a direct and systematic comparison between the latter model and the blast-wave feedback model is still missing. Therefore at present it is unclear which of the two models performs best against a large set of properties measured for real disk galaxies, especially it is unknown how the two models compare when they are used in cosmological simulations starting with identical initial conditions. Such a comparison would certainly be of great benefit in order to ponder in a critical way the conceptual modeling behind the two different methods.
Finally, the fact that cosmological simulations with blast-wave feedback reproduce the observed stellar mass-metallicity relation 100 suggests that this kind of sub-grid model not only provides a reasonable description of the star formation process but also of the associated metal enrichment (in the model metals are liberated when supernovae type I and type II explode, as well as via stellar winds 86) and mixing processes in galaxies. It is important to note that with this model of feedback galaxies with a rotational velocity > 50-80 km/s do not experience major gas "blowouts" and are able to retain a relatively large gas fraction within their virial radius. Rather supernovae feedback makes star formation relatively inefficient in small galaxies, making them gas rich and more metal poor, as the metals produced in stellar explosions are diluted over a larger gas fraction. This result opens the door to the possibility of using the blast-wave feedback model to study the photometric properties of very high redshift galaxies, where the poorly known amount of metals in the gas component can strongly affect their observational properties.