In this section I shall discuss some issues relating to Bondi-Hoyle-Lyttleton flow which are of particular interest.
The simple idealisation of Bondi-Hoyle-Lyttleton flow cannot persist for long. The accretor is not only increasing its mass - it is accumulating momentum as well. Eventually, it should be accelerated to being co-moving with the gas flow. A full calculation is not straightforward, but dimensional considerations suggest
 |
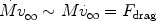(33) |
Please note, that the ~ in this equation is very approximate. However, equation 33 suggests that the accreting body will be brought to rest with respect to the flow on the mass doubling timescale. This is obviously a problem if the accretor is to change its mass appreciably. As we shall see later, this has lead to most research into Bondi-Hoyle-Lyttleton accretion being concentrated into the study of binaries. In such cases, the momentum difference can be `paid' by a change in orbit.
The drag does not originate as a form of `wind' resistance pressing directly on the accretor. This is for two reasons
Instead, the drag arises from the gravitational focusing of material behind the accretor. Since more material is present on the downstream side, the gravitational attraction of the downstream side is larger, 1 and exerts a drag force. Chandrasekhar (1943) was the first to consider this problem - called `dynamical friction' - for a collisionless fluid. An extended (and more recent) discussion of the problem is given by Binney and Tremaine (1987). Dokuchaev (1964) discussed the problem for a gaseous medium. The matter of drag is also mentioned by Ruderman and Spiegel (1971), who propose
 |
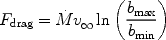(34) |
where bmin and bmax are cut-off radii for the gravitational force. Yabushita (1978) suggested that a suitable value for the outer cut-off for a flow with pressure would be the point where the pressure in the wake became equal to the background pressure (the inner cut-off radius is usually taken to be the radius of the accretor itself).
Values for the drag force given by Shima et al. (1985), Shankar et al. (1993), Ruffert and Arnett (1994) suggest that the drag force is no more than a factor of ten larger than the crude estimate of equation 33. The precise drag value has a tendency to fluctuate anyway - Bondi-Hoyle-Lyttleton flow is not stable.
Even in the axisymmetric case, there is no particular reason to believe
that Bondi-Hoyle-Lyttleton flow should be stable.
The binding energy test of equation 6
is made for gas flowing away from the accretor.
If this material is going to be accreted, it needs to turn around
somehow and fall towards the point mass.
This must happen in some sort of accretion column, of the type
first considered by
Bondi
and Hoyle (1944).
As noted above, the work of
Cowie
(1977)
found that this wake should be unstable.
A `shock cone' must surround the wake, in which the flow loses
its 
velocity before it
encounters the axis (see also Wolfson
(1977a,
b).
The high densities expected for the wake mean that this shock is likely
to heat the gas. Gas pressure could then be expected to drive
oscillations close to the stagnation point.
Bondi-Hoyle-Lyttleton flow around small accretors has been studied by
Koide et
al. (1991).
This paper notes that that the `accreting body is so small that a
part of the accreting gas sometimes misses the target object and
flows towards the upstream as a jet.'
This is obviously a rather unstable condition, and leads to the
accretion flow `sloshing' back and forth around the point mass.
The accretion rate fluctuates too, although the time averaged
rate is still close to the Bondi-Hoyle value.
When the condition of axisymmetry is relaxed, even more instabilities become possible. Matsuda et al. (1987); Fryxell and Taam (1988); Taam and Fryxell (1988) performed two dimensional simulations of the Bondi-Hoyle-Lyttleton geometry, with the condition of axisymmetry relaxed, and a density and/or velocity gradient imposed on the upstream flow. All three papers found that a `flip-flop' instability resulted, with the wake oscillating back and forth in a manner reminiscent of a von Kármán vortex street. Matsuda et al. (1991) suggested that the instability was intrinsic to the accretion flow, since it was found to develop even under the conditions first considered by Hoyle and Lyttleton (1939). Another detailed study of the `flip-flop' instability for the 2D case for isothermal gas is that of Shima et al. (1998). The code used was specifically designed to conserve angular momentum and to permit very high resolution in the inner portions of the grid. They suggest that some of the resolution dependence of the instability found by earlier work was due to the use of codes which conserved linear momentum, and caution against the results obtained by such codes.
Such a spectacular instability naturally prompted an intense theoretical investigation. Soker (1990) extended the earlier work of Cowie (1977) to include tangential oscillations. The analysis is based on the assumption of a pressure free flow, and the expressions derived for the tangential behaviour also require the flow to be 2D and planar. The radial instability noted by Cowie found to be independent of the incoming material. Any radial oscillation in the wake would grow, although the growth timescale was much longer than the oscillation timescales. The tangential modes (corresponding to the `flip-flop' instability) behaved in a similar manner. Soker also predicted that the instability should be milder in the 3D case. In Soker (1991), a numerical study of the coupling between the radial and tangential oscillations was made. The radial modes, corresponding to large density and velocity fluctuations were excited far beyond the linear regime, while the tangential oscillations remained linear. While the mass accretion rate showed corresponding fluctuations, the time averaged accretion rate was similar (although smaller) than the prediction of equation 7. Livio et al. (1991) added a simple analysis of the shock cone surrounding the wake seen in numerical simulations. Instabilities were found in both the planar 2D and full 3D cases, although the authors note that the instability should be milder in the 3D case (a point also made by Soker (1990)).
The major weakness of all simulations of the `flip-flop' instability mentioned so far is that they fundamentally change the geometry of the problem. In order to simulate non-axisymmetric flow in two dimensions, the flow has to be assumed to be planar. This changes the shape of the accretor from a sphere to a cylinder. The equations of fluid dynamics are non-linear, and are notorious for their resolute refusal to yield to a proof of solution uniqueness (Fefferman, 2000). There is therefore no particular reason to expect the 2D planar simulations to be characteristic of the true solution in 3D. The simulations of Ruffert suggest that the `flip-flop' instability is an artifact of 2D planar flow.
Foglizzo and Ruffert (1997, 1999) attempted to model the instabilities observed in the earlier numerical work of Ruffert. The first of these papers constructs stationary models, while the second contains a stability analysis. The origin of the instability was the bow shock generally seen in numerical simulations. This produces entropy gradients in the flow, which allows Rayleigh-Taylor and Kelvin-Helmholtz instabilities to grow. Foglizzo and Ruffert concluded that the instability should be stronger if
values)
They found that the instability should be non-axisymmetric, and
start at around =
/
2 and close to the accretor.
Foglizzo
and Tagger (2000)
describe the instability as `entropic-acoustic,'
where entropy perturbations introduced by a shock propagate back
to the shock via sound waves.
These then trigger new entropy perturbations.
Suppose the conditions at infinity are not uniform, but instead a
density and/or velocity gradient is present.
This means that the flow within a cylinder of radius
HL
possesses angular momentum about the accretor.
How much of this reaches the accretor?
Early calculations (Dodd and McCrea, 1952; Illarionov and Sunyaev, 1975; Shapiro and Lightman, 1976 Wang, 1981;) suggested that most of this angular momentum would accrete. However, Davies and Pringle (1980) pointed out that only material which had lost most of its angular momentum would be able to settle onto a small accretor. They developed a simple analytic model for small density and velocity gradients (if the gradients become large, then the flow ceases to behave in the manner described by Bondi, Hoyle and Lyttleton). Davies and Pringle found that the mass accretion rate should be unaffected, and there should be no accretion of angular momentum.
Such confusion calls for numerical work.
Ruffert
and Anzer (1995)
presented a sample 3D simulation of accretion under such conditions.
They found that about 70% of the angular momentum available (as calculated
by Shapiro
and Lightman (1976))
would be accreted. Ruffert extended this calculation with papers in
1997 (covering velocity gradients)
and 1999 (studying density gradients).
The mass accretion was not affected much, while the angular momentum
accretion rate varied between 0% and 70% of the value suggested
by Shapiro
and Lightman (1976).
Smaller accretors gave less stable flow, but none were as violently
unstable as the `flip-flop' instability observed in 2D planar simulations.
Ruffert noted that a very small accretor will
not be able to accrete all of the angular momentum within
HL,
but was unable to test such a case, due to the vast computational load
involved in such a simulation.
Where there is accretion, there will be an accretion luminosity. 2 Radiative feedback has the potential to alter the Bondi-Hoyle-Lyttleton flow, and a number of workers have studied this.
Most work has concentrated on the problem of radiative feedback in X-ray binaries. This is a fairly straightforward application, since the constancy of the Thompson cross section makes the transfer problem intrinsically grey.
Blondin et al. (1990) simulated a compact object accreting an O star wind (forming an X-ray binary). Radiative heating was included (it was relevant to the radiation-driven wind), but the radiation force of the X-rays was neglected. The gas was assumed to be optically thin and in ionisation equilibrium. The wake was found to be unstable, oscillating back and forth. Despite these, the accretion rates were broadly consistent with that expected from a Bondi-Hoyle type analysis (some modifications were necessary to allow for the geometry of the binary). A later study of the same problem was made by Taam et al. (1991). This work included the effect of radiation pressure, but the flow was still assumed to be optically thin to electron scattering. Radiation pressure was then negligible except in the wake. This paper contained short section considering the accretion of an optically thin gas subject to radiation pressure. This led to the prediction that the flow would be unstable to oscillations if the accretion rate exceeded one third of the Eddington Limit.
Kley et al. (1995) were interested in the application of Bondi-Hoyle-Lyttleton accretion following a nova explosion in a binary. The radiation field was simulated using flux limited diffusion, and analytic approximations to opacity values. Their simulations had quite a complicated model for the accretor, including an envelope. Radiation pressure was found to be critical to simulating the flow (heating was included in all calculations, but the radiation pressure was omitted from some). For hot, optically thick flow, including radiation pressure made the flow subsonic and substantially reduced the drag. However, the accretion rate was found to be low (much less than the predictions of Bondi-Hoyle theory) in all cases.
If the accreting object is a neutron star or a black hole, relativistic effects are likely to become important. However, relativistic hydrodynamics is generally recognised to be a non-trivial problem, and relatively little work has been done on Bondi-Hoyle-Lyttleton accretion for relativistic flows.
An early study by Petrich et al. (1989) found broad agreement between the Newtonian and relativistic cases. Font and Ibáñez (1998b) performed axisymmetric calculations in a Schwarzschild metric. The passage of time gave more powerful computers, enabling simulations to be run with higher resolution than Petrich et al. Most of the accretion rates found were similar to the Newtonian estimates, but some were an order of magnitude or so higher. No signs of instability were found. Font and Ibáñez (1998a) relaxed the assumption of axisymmetry, but still found the flow to be steady. However, the authors note that they were unable to push the simulation parameters very far.
Font et al. (1999) simulated Bondi-Hoyle-Lyttleton flow onto a rotating (Kerr) black hole. Two forms of the metric were used, to differentiate between numerical and physical effects. They found that rotational effects were confined to a region close to the hole. Their flows remained steady.
1 This is ignoring the mathematical impossibility of an infinite, uniform medium for the unperturbed case Back.
2 Barring certain cases of finely tuned accretion onto a black hole Back.