In this paper we attempt to constrain the acceleration models based on the observations described in the papers by Durret et al. (2008), Rephaeli et al. (2008) and Ferrari et al. (2008) - Chapters 4-6, this volume, and the required spectrum of the accelerated electrons shown in Fig. 6 of Petrosian et al. 2008 - Chapter 10, this volume. However, before addressing these details we first compare various acceleration processes and stress the importance of plasma waves or turbulence (PWT) as an agent of scattering and acceleration, and then describe the basic scenario and equations for treatment of these processes. As pointed out below there is growing evidence that PWT plays an important role in acceleration of particles in general, and in clusters of galaxies in particular. The two most commonly used acceleration mechanisms are the following.
1.1. Electric field acceleration
Electric fields parallel to magnetic fields can accelerate charged
particles and can arise as a result of magnetic field reconnection in a
current sheet or other situations. For fields less than the so-called
Dreicer field, defined as
ED = kT / (e
Coul), where
 |
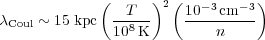(1) |
is the collision (electron-electron or proton-proton) mean free
path 1, the rate of
acceleration is less than the rate of collision
losses and only a small fraction of the particles can be accelerated
into a non-thermal tail of energy E <
LeED. For the ICM ED ~
10-14 V cm-1 and L ~ 1024 cm so
that sub-Dreicer fields can
only accelerate particles up to 100's of keV, which is far below the
10's of GeV electrons required by observations. Super-Dreicer fields,
which seem to be present in many simulations of reconnection
(Drake 2006,
Cassak et
al. 2006,
Zenitani
& Hoshino 2005),
accelerate particles at
a rate that is faster than the collision or thermalisation time
therm. This can
lead to a runaway and an unstable electron distribution which,
as shown theoretically, by laboratory experiments and by the above
mentioned simulations, most probably will give rise to PWT
(Boris et
al. 1970,
Holman 1985).
In summary the electric fields arising as a result of reconnection cannot be the sole agent of acceleration in the ICM, because there are no large scale magnetically dominated cosmological flows, but it may locally produce an unstable particle momentum distribution which will produce PWT that can then accelerate particles.
Nowadays this process has been divided into two kinds. In the original
Fermi process particles of velocity v moving along magnetic field
lines (strength B) with a pitch angle cosµ undergo
random scattering by moving agents with a velocity u. Because the
head (energy gaining) collisions are more probable than trailing (energy
losing) collisions, on average, the particles gain energy at a rate
proportional to
(u / v)2 Dµµ, where
Dµµ is the pitch angle diffusion rate. This,
known as a second order Fermi process
is what we shall call stochastic acceleration. In general, the most
likely agent for scattering is PWT. An alternative process is what is
commonly referred to as a first order Fermi process, where the
actual acceleration occurs when particles
cross a shock or any region of converging flow. Upon crossing the shock
the fractional gain of momentum
p / p
ush / v. Ever since the 1970's, when
several authors demonstrated that a very simple version of this process
leads to a power law spectrum that agrees approximately with
observations of the cosmic rays, shock acceleration is commonly invoked
in space and astrophysical plasmas. However, this simple model, though
very elegant, has some shortcomings specially when applied to electron
acceleration in non-thermal radiating sources. Moreover, some of the
features that make this scenario for acceleration of cosmic rays
attractive are not present in most radiating sources where one needs
efficient acceleration of electrons to relativistic energies from a low
energy reservoir.
The original, test particle theory of diffusive shock acceleration (DSA), although very elegant and independent of geometry and other details (e.g. Blandford & Ostriker 1978) required several conditions such as injection of seed particles and of course turbulence. A great deal of work has gone into addressing these aspects of the problem and there has been a great deal of progress. It is clear that nonlinear effects (see e.g. Drury 1983, Blandford & Eichler 1987, Jones & Ellison 1991, Malkov & Drury 2001) and losses (specially for electrons) play an important role and modify the resultant spectra and efficiency of acceleration. Another important point is the source of the turbulence or the scattering agents. A common practice is to assume Bohm diffusion (see e.g. Ellison et al. 2005). Second order acceleration effects could modify the particle spectra accelerated by shocks (see e.g. Schlickeiser et al. 1993, Bykov et al. 2000). Although there are indications that turbulence may be generated by the shocks and the accelerated particle upstream, many details (e.g. the nature and spectrum of the turbulence) need to be addressed more quantitatively. There has been progress on the understanding of generation of the magnetic field and turbulence on strong shocks (Bell & Lucek 2001, Amato & Blasi 2006, Vladimirov et al. 2006) as required in recent observations of supernova remnants (see e.g. Völk et al. 2005). There is also some evidence for these processes from observations of heliospheric shocks (see e.g. Kennel et al. 1986, Ellison et al. 1990). Basic features of particle acceleration by cosmological shocks were discussed by Bykov et al. 2008a - Chapter 7, this volume, so we will concentrate here on the stochastic acceleration perspective.
The PWT needed for scattering can also accelerate particles
stochastically with a rate
DEE / E2, where
DEE is the energy diffusion coefficient, so
that shocks may not be always necessary. In low beta plasmas,
p
= 2(vs / vA)2 < 1,
where the Alfven velocity vA = (B2 /
4
)1/2,
the sound velocity
vs = (kT / m)1/2,
= nm is
the mass density and n is the number density
of the gas, and for relativistic particles the PWT-particle interactions
are dominated by Alfvenic turbulence, in which case the rate of energy
gain
DEE / E2 = (vA /
v)2 Dµµ <<
Dµµ, so that the first order
Fermi process is more efficient. However, at low energies and/or in very
strongly magnetised plasmas, where vA can exceed
c, the speed of light
2, the acceleration rate
may exceed the scattering rate (see
Pryadko &
Petrosian 1997),
in which case low energy electrons are accelerated more efficiently by
PWT than by shocks. 3
Irrespective of which process dominates the particle acceleration, it is clear that PWT has a role in all of them. Thus, understanding of the production of PWT and its interaction with particles is extremely important. Moreover, turbulence is expected to be present in most astrophysical plasmas including the ICM and in and around merger or accretion shocks, because the ordinary and magnetic Reynolds numbers are large. Indeed turbulence may be the most efficient channel of energy dissipation. In recent years there has been a substantial progress in the understanding of MHD turbulence (Goldreich & Sridhar 1995, Goldreich & Sridhar 1997, Lithwick & Goldreich 2003, Cho & Lazarian 2002, Cho & Lazarian 2006). These provide new tools for a more quantitative investigation of turbulence and the role it plays in many astrophysical sources.
1 The proton-proton or ion-ion mean free
path will be slightly smaller because of the larger value of the Coulomb
logarithm ln
~ 40
in the ICM.
Back.
2 Note that the Alfven group velocity vg = c [vA2 / (vA2 + c2)]1/2 is always less than c. Back.
3 In practice, i.e. mathematically, there is little difference between the two mechanisms (Jones 1994), and the acceleration by turbulence and shocks can be combined (see below). Back.