2. TURBULENCE AND STOCHASTIC ACCELERATION

2.1. Basic scenario

The complete picture of stochastic acceleration by PWT is a complex and not yet fully understood or developed process. However, one might envision the following scenario.

Turbulence or plasma waves can be generated in the ICM on some macroscopic scale L ~ 300 kpc (some fraction of the cluster size or some multiple of galactic sizes) as a result of merger events or by accretion or merger shocks. That these kind of motions or flows with velocity comparable to or somewhat greater than the virial velocity u_L ~ 1000 km s^-1 will lead to PWT is very likely, because in the ICM the ordinary Reynolds number R_e = u_LL / >> 1. Here ~ v_{th scat}/3 is the viscosity, v_th = (kT / m)^1/2 ~ u_L(T / 10⁸)^1/2 and _scat is the mean free path length. The main uncertainty here is in the value of _scat. For Coulomb collisions _scat ~ 15 kpc (Eq. 1) and R_e ~ 100 is just barely large enough for generation of turbulence. However, in a recent paper Brunetti & Lazarian (2007) argue that in the presence of a magnetic field of B ~ µG, v_A ~ 70 (B / µG)(10^-3 cm^-3 / n)^1/2 km s^-1 is much smaller than v_th so that the turbulence will be super-Alfvénic, in which case the mean free path may be two orders of magnitude smaller ⁴ yielding R_e ~ 10⁴. We know this also to be true from a phenomenological consideration. In a cluster the hot gas is confined by the gravitational field of the total (dark and 'visible') matter. Relativistic particles, on the other hand, can cross the cluster of radius R on a timescale of T_cross = 3 × 10⁶(R / Mpc) yr and can escape the cluster (see Fig. 4 below), unless confined by a chaotic magnetic field or a scattering agent such as turbulence with a mean free path _scat << R. If so, then the escape time T_esc ~ T_cross(R / _scat) = T_cross² / _scat. The curve marked with arrows in this figure shows the maximum value of the required _scat so that the escape time is longer than the energy loss time _loss. As is evident from this figure, for a GeV electron to be confined for a Hubble timescale, or T_esc ~ 10¹⁰ yr, we need _scat ~ 3 × 10⁴ yr or _scat < 10 kpc. This could be the case in a chaotic magnetic field and/or in the presence of turbulence. Some observations related to this are discussed by Petrosian et al. 2008 - Chapter 10, this volume; see also Vogt & Enßlin (2005). Numerous numerical simulations also agree with this general picture. There is evidence for large scale bulk flows in the simulations of merging clusters (e.g. Roettiger et al. 1996, Ricker & Sarazin 2001), and that these are converted into turbulence with energies that are a substantial fraction of the thermal energy of the clusters (e.g. Sunyaev et al. 2003, Dolag et al. 2005). For more details see Brunetti & Lazarian (2007).

Once the PWT is generated it can undergo two kind of interactions. The first is dissipationless cascade from wave vectors k_min ~ L^-1 to smaller scales. The cascade is gouverned by the rates of wave-wave interactions. For example, in the case of weak turbulence, that can be considered as a superposition of weakly interacting wave packets, the three wave interactions can be represented as

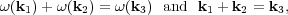(2)

where k is the wave vector, and the wave frequency, (k), is obtained from the plasma dispersion relation. One can interpret Eq. 2 as energy-momentum conservation laws for weakly coupled plasma waves in a close analogy to the optical waves. The interaction rates can be represented by the wave diffusion coefficient D_ij or the cascade time _cas ~ k² / D_ij. The largest uncertainty is in the diffusion coefficient. Because of the nonlinear nature of the interactions this coefficient depends on the wave spectrum W(k). As mentioned above there has been considerable progress in this area in the past two decades and there are some recipes how to calculate the diffusion coefficients.

The second is damping of the PWT by wave-particle interaction which terminates the dissipationless cascade, say at an outer scale k_max when the damping rate (k_max) = _cas^-1(k_max). The range k_min < k < k_max is called the inertial range. The damping rate can be obtained from the finite temperature dispersion relations (see below). The energy lost from PWT goes into heating the background plasma and/or accelerating particles into a non-thermal tail. These processes are described by the diffusion coefficients D_EE and D_µµ introduced above. These coefficients are obtained from consideration of the wave-particle interactions which are often dominated by resonant interactions, specially for low beta (magnetically dominated) plasma, such that

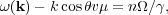(3)

for waves propagating at an angle with respect to the large scale magnetic field, and a particle of velocity v, Lorentz factor , pitch angle cosµ and gyrofrequency = eB / mc. Both cyclotron (the term in the right hand side of Eq. 3) and Cerenkov resonance (the second term in the left hand side) play important roles in the analysis (see for details e.g. Akhiezer et al. 1975). Here, when the harmonic number n (not to be confused with the density) is equal to zero, the process is referred to as the transit time damping. For gyroresonance damping by waves propagating parallel to the field lines ( = 0) n = ± 1. For obliquely propagating waves, in principle one gets contributions from all harmonics n = ± 1, ± 2, …, but for practical purposes most of the contribution comes from the lowest harmonics n = ± 1 (see Pryadko & Petrosian 1998).

2.2. Dispersion relations

It is clear from the above description that at the core of the evaluation of wave-wave or wave-particle interactions (and all the coefficients of the kinetic equations described below) lies the plasma dispersion relation (k). It describes the characteristics of the waves that can be excited in the plasma, and the rates of wave-wave and wave-particle interactions.

In the MHD regime for a cold plasma

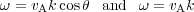(4)

for the Alfvén and the fast (magneto-sonic) waves, respectively. Beyond the MHD regime a multiplicity of wave modes can be present and the dispersion relation is more complex and is obtained from the following expressions (see e.g. Sturrock 1994):

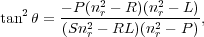(5)

where n_r = kc / is the refractive index, S = 1/2(R + L), and

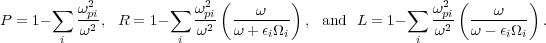(6)

Here _pi² = 4 n_i q_i² / m_i and _i = |q_i|B / m_i c are the plasma and gyro frequencies, _i = q_i / |q_i|, and n_i, q_i, and m_i are the density, charge, and mass of the background particles. For fully ionised plasmas such as that in the ICM it is sufficient to include terms due to electron, proton and particles. Fig. 1 shows the dispersion surfaces (depicted by the curves) obtained from the above expressions along with the resonant planes in the (, k_||, k) space. Intersections between the dispersion surfaces and the resonant planes define the resonant wave-particle interactions and the particle kinetic equation coefficients. One can also envision a similar graphic description of the three wave interactions (Eq.2) using the intersections of the curved dispersion surfaces. However, such calculations have been carried out only in the MHD regime using the simple relations of Eq. 4, which is already a complicated procedure (see e.g. Chandran 2005, Luo & Melrose 2006).

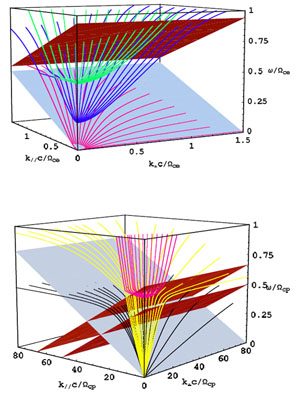Figure 1. Dispersion relation (curves) surfaces for a cold fully ionised H and He (10% by number) plasma and resonance condition (flat) surfaces showing the regions around the electron (top panel) and proton (bottom panel) gyro-frequencies. Only waves with positive k||, k (or 0 < < /2) are shown. The mirror image with respect to the (, k) plane gives the waves propagating in the opposite direction. From high to low frequencies, we have one of the electromagnetic branches (green), upper-hybrid branch (purple), lower-hybrid branch, which also includes the whistler waves (pink), fast-wave branches (yellow), and Alfvén branch (black). The effects of a finite temperature modify these curves at frequencies ~ kvth, where vth = (2kT / m)1/2 is the thermal velocity (see e.g. André 1985). The resonance surfaces are for electrons with v = 0.3c and |µ| = 1.0 (top panel: upper, brown n = 1, lower, light blue n = 0) and 4He (bottom panel: middle, brown n = 1) and 3He (bottom panel: upper, brown n = 1) ions with |µ| = 1.0 and v = 0.01c. The resonance surfaces for the latter two are the same when n = 0 (bottom panel: lower).

The above dispersion relations are good approximations for low beta plasmas but in the ICM the plasma beta is large:

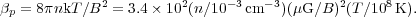(7)

For high beta plasmas the dispersion relation is modified, specially for higher frequencies ~ kv_th. For example, in the MHD regime, in addition to the Alfvén mode one gets fast and slow modes with the dispersion relation (see e.g. Sturrock 1994)

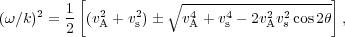(8)

and the more general dispersion relation (Eq. 5) is modified in a more complicated way (see e.g. André 1985 or Swanson 1989). The finite temperature imparts an imaginary part _i to the wave frequency that gives the damping rate (k) as long as _i < _r, the real part of the frequency ⁵. For more details see e.g. Barnes & Scargle (1973), Swanson (1989), Pryadko & Petrosian (1998), Pryadko & Petrosian (1999), Cranmer & Van ballegooijen (2003), Brunetti & Lazarian (2007). In general, these rates and the modification of the dispersion relation are known for Maxwellian (sometimes anisotropic) energy distributions of the plasma particles. For non-thermal distributions the damping rates can be evaluated as described Petrosian et al. (2006) using the coupling described in Eq. 11 below.

2.3. Kinetic equations and their coefficients

2.3.1. Wave equation

Adopting the diffusion approximation (see e.g. Zhou & Matthaeus 1990), one can obtain the evolution of the spatially integrated wave spectrum W(k, t) from the general equation

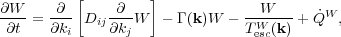(9)

where 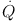^W is the rate of generation of PWT at k_min, T_esc^W is the escape time, and D_ij and describe the cascade and damping of the waves. The calculation of the damping rate is complicated but as described above it is well understood, but there are many uncertainties about the treatment of the cascade process or the form of D_ij. This is primarily because of incompleteness of the theoretical models and sufficient observational or experimental data. There are some direct observations in the Solar wind (e.g. Leamon et al. 1998) and indirect inferences in the interstellar medium (see e.g. Armstrong et al. 1995). There is some hope (Inogamov & Sunyaev 2003) of future observations in the ICM. Attempts in fitting the Solar wind data have provided some clues about the cascade diffusion coefficients (see Leamon et al. 1999, Jiang et al. 2007).

2.3.2. Particle acceleration and transport

As described by Petrosian et al. 2008 - Chapter 10, this volume, the general equation for treatment of particles is the Fokker-Planck equation which for ICM conditions can be simplified considerably. As pointed out above we expect a short mean free path and fast scatterings for all particles. When the scattering time _scat = _scat / v ~ <1 / D_µµ> is much less than the dynamic and other timescales, the particles will have an isotropic pitch angle distribution. The pitch-angle averaged and spatially integrated particle distribution is obtained from ⁶

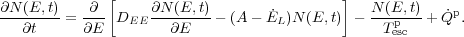(10)

Here D_EE / E² is the energy diffusion, due to scattering by PWT as described above and due to Coulomb collisions as discussed by Petrosian et al. 2008 - Chapter 10, this volume, A(E) / E ~ D_EE / E², with (E) = (2 - ^-2) / (1 + ^-1) is the rate of direct acceleration due to interactions with PWT and all other agents, e.g., direct first order Fermi acceleration by shocks, 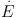_L / E is the energy loss rate of the particles (due to Coulomb collisions and synchrotron and IC losses, see Fig. 4 in Petrosian et al. 2008 - Chapter 10, this volume), and 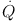^p and the term with the escape times T_esc^p describe the source and leakage of particles ⁷.

The above two kinetic equations are coupled by the fact that the coefficients of one depend on the spectral distribution of the other; the damping rate of the waves depends on N(E,t) and the diffusion and accelerations rates of particles depend on the wave spectrum W(k, t). Conservation of energy requires that the energy lost by the waves 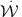_tot (k) W(k)d³k must be equal to the energy gained by the particles from the waves; 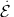= [A(E) - A_sh]N(E)d E. Representing the energy transfer rate between the waves and particles by (k, E) this equality implies that

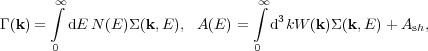(11)

where we have added A_sh to represent contributions of other (non-stochastic acceleration) processes affecting the direct acceleration, e.g., shocks.

If the damping due to non-thermal particles is important then the wave and particle kinetic equations (9) and (10) are coupled and attempts have been made to obtain solutions of the coupled equations (Miller et al. 1996, Brunetti & Blasi 2005). However, most often the damping rate is dominated by the background thermal particles so that the wave and non-thermal particle kinetic equations decouple. This is a good approximation in the ICM when dealing with relativistic electrons so that for determination of the particle spectra all we need is the boundaries of the inertial range (k_min, k_max), the wave spectral index q in this range (most likely 5/3 < q < 3/2), and the shape of the spectrum above k_max which is somewhat uncertain (see Jiang et al. 2007).

⁴ Plasma instabilities, possibly induced by the relativistic particles, can be another agent of decreasing the effective particle mean free path (Schekochihin et al. 2005). Back.

⁵ Note that the 'thermal' effects change _r only slightly so that often the real part, the resonant interaction rate and the particle diffusion coefficients can be evaluated using the simpler cold plasma dispersion relation depicted in Fig. 1. Back.

⁶ The derivation of this equation for the stated conditions and some other details can be found in the Appendix. Back.

⁷ in what follows we will assume that the waves are confined to the ICM so that T_esc^W and in some cases we will assume no escape of particles and let T_esc^p . Back.