9. WIDE AREA SURVEYS AND LARGE SCALE STRUCTURE

Extragalactic radio sources are well suited to probe the large-scale structure of the Universe: detectable over large cosmological distances, they are unaffected by dust extinction, and can thus provide an unbiased sampling of volumes larger than those usually probed by optical surveys. On the other hand, their 3D space-distribution can be recovered only in the very local Universe (z 0.1; see Peacock & Nicholson 1991, Magliocchetti et al. 2004) because the majority of radio galaxies detected in the available large-area, yet relatively deep, surveys, carried out at frequencies 1.4 GHz, have very faint optical counterparts, so that redshift measurements are difficult. As a result, only the angular (2D) clustering can be measured for the entire radio AGN population. High-frequency surveys have much higher identification rates (Sadler et al. 2006), suggesting that this difficulty may be overcome when such surveys cover sufficient sky and are linked to wide-area redshift surveys.

9.1. The angular correlation function and its implications

Just the basic detection of clustering in the 2D distribution of radio sources proved to be extremely difficult (e.g. Webster 1976, Seldner & Peebles 1981, Shaver & Pierre 1989) because at any flux-density limit, the broad luminosity function translates into a broad redshift distribution, strongly diluting the spatial correlations when projected onto the sky. Only with the advent of deep radio surveys covering large areas of the sky, FIRST (Becker et al. 1995), WENSS (Rengelink et al. 1997), NVSS (Condon et al. 1998), and SUMSS (Mauch et al. 2003), did it become possible to detect the angular clustering of these objects with high statistical significance: see Cress & Kamionkowski (1998) and Magliocchetti et al. (1998), Magliocchetti et al. (1999), Blake & Wall (2002a) for FIRST; Blake & Wall (2002b), Blake & Wall (2002a) and Overzier et al. (2003) for NVSS; Rengelink (1999) for WENSS; and Blake et al. (2004b). Even then there remained difficulties of interpretation due to spurious correlation at small angular scales caused by the multiple-component nature of extended radio sources (Blake & Wall 2002b); the raw catalogues constructed from these large surveys list components of sources rather than single `assembled' sources. Amongst the cited surveys, NVSS is characterized by the most extensive sky coverage and can thus provide the best clustering statistics, despite its somewhat higher completeness limit (~ 3 mJy vs ~ 1 mJy of FIRST). The two-point angular correlation function w(), measured for NVSS sources brighter than 10 mJy, is well described by a power-law of slope -0.8 extending from ~ 0.1 degrees up to scales of almost 10 degrees (Blake & Wall 2002a). A signal of comparable amplitude and shape was detected in the FIRST survey at the same flux density limit, on scales of up to 2-3 degrees (see e.g. Magliocchetti et al. 1998, Magliocchetti et al. 1999), while at larger angular separations any positive clustering signal - if present - is hidden by the Poisson noise.

Most of the analyses performed so far with the aim of reproducing the clustering of radio galaxies (see e.g. Blake & Wall 2002b, Blake & Wall 2002a, Overzier et al. 2003) assumed a two-point spatial correlation function of the form _rg(r) = (r / r₀)^-. The power-law shape is in fact preserved when projected onto the sky (Limber 1953), so that the observed behaviour of the angular correlation is well recovered. The correlation length r₀ was found to lie in the range 5-15 Mpc, the large range reflecting the uncertainties in both the redshift distribution of the sources and the time-evolution of clustering. Despite the wide range in measurement of r₀, the above results suggest that radio galaxies are more strongly clustered than optically-selected galaxies.

A deeper examination of the power-law behaviour of the angular two-point correlation function up to scales of the order of ~ 10° highlights interesting issues. Within the Cold Dark Matter paradigm of structure formation, the spatial correlation function of matter displays a sharp cut-off near a comoving radius of r ~ 100 Mpc, which at the average redshift for radio sources <z> ~ 1, corresponds to angular separations of only a few (~ 1°-2°) degrees. This is in clear contrast to the observations of the angular two-point correlation function. The question is how to reconcile the clustering properties of these sources with the standard scenario of structure formation. Some authors have tried to explain the large-scale positive tail of the angular correlation function w() as due to a high-density local population of star-forming galaxies Blake et al. (2004a). Others Magliocchetti et al. (1999) suggested that the results can be reproduced by a suitable choice of the time-evolution of the bias parameter, i.e. the way radio galaxies trace the underlying mass distribution. The first hypothesis can be discarded on the basis of more recent determinations of the space density of local star-forming galaxies with a 1.4-GHz radio counterpart (e.g. Magliocchetti et al. 2002, Sadler et al. 2002, Mauch & Sadler 2007). Even the second approach, although promising, suffers a number of limitations due to both theoretical modelling and quality of data then available.

Theoretical predictions for the angular two-point correlation function of a given class of objects using Limber (1953) equation

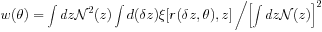(22)

require two basic ingredients: their redshift distribution, (z), i.e. the number of objects brighter than the flux limit of the survey as a function of redshift, and the value of the bias factor as a function of redshift, b(z). In equation (22), r(z, ) represents the comoving spatial distance between two objects located at redshifts z and z + z and separated by an angle on the sky. For a flat universe and in the small-angle approximation (still reasonably accurate for scales of interest here, 0.3° 10°)

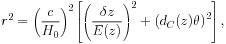(23)

with

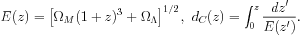(24)

On sufficiently large scales, where the clustering signal is produced by galaxies residing in distinct dark-matter halos and under the assumption of a one-to-one correspondence between sources and their host halos, the spatial two-point correlation function can be written as the product of the correlation function of dark matter, _DM, times the square of the bias parameter, b (Matarrese et al. 1997, Moscardini et al. 1998):

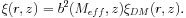(25)

Here, M_eff is the effective mass of the dark matter haloes in which the sources reside and b is derived in the extended Press & Schechter (1974) formalism according to the prescriptions of Sheth & Tormen (1999).

Negrello et al. (2006) adopted the (z) from Dunlop & Peacock (1990)'s pure luminosity evolution model. If the effective mass of the dark matter haloes in which the sources reside does not depend on cosmic time, as found for optically-selected quasars (Porciani et al. 2004, Croom et al. 2004), the predicted angular correlation function badly fails to reproduce the observed one. This is because contributions to w() on a given angular scale come from both local, relatively close pairs of sources and from high-redshift, more distant ones. But for z 1 angular scales 2° correspond to linear scales where the correlation function is negative. Since the contribution of distant objects is overwhelming, we expect negative values of w(), while observations give us positive values.

The only way out appears to be a damping down of the contribution to w() of high-z sources, and this can only be achieved through b(z). Negrello et al. (2006) found that the w() data can be reproduced by assuming an epoch-dependent effective mass proportional to the mass scale at which the matter-density fluctuations collapse to form bound structures. Such mass decreases with increasing redshift, thus abating the negative high-z contributions to w(). This assumption may be justified - locally, AGN-powered radio galaxies are found mainly in very dense environments such as groups or clusters of galaxies, and the characteristic mass of virialized systems indeed decreases with increasing redshift. The best fit to the data was obtained for a high value of the local effective mass, M_eff(z = 0) 10¹⁵ M / h. However the CENSORS data (Brookes et al. 2008) have shown that the redshift distribution peaks at lower redshifts than predicted by Dunlop & Peacock (1990) PLE model (Fig. 11). Using a smooth description of the CENSORS redshift distribution

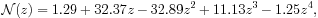(26)

the best fit is obtained with a somewhat lower value for the local effective mass, M_eff(z = 0) 10^14.5 M / h (Fig. 13).

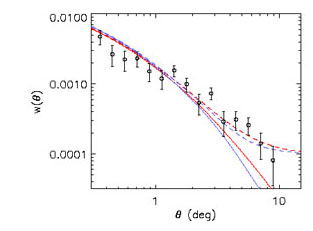Figure 13. Two-point angular correlation function of NVSS sources with S1.4GHz 10 mJy as measured by Blake & Wall (2002b) compared with the model by Negrello et al. (2006) (red curves) and with the updated model (blue curves) fitting the redshift distribution by Brookes et al. (2008). The dashed curves include the contribution of a constant offset = 0.0001 to w() in order to account for the effect of possible spurious density gradients in the survey.

9.2. Integrated Sachs-Wolfe (ISW) effect

The ISW effect describes the influence of the evolution of the gravitational potential in time-variable, linear, metric perturbations on CMB photons that traverse them. When the CMB photons enter an overdensity they are gravitationally blue-shifted, and they are red-shifted when they emerge. In an Einstein-de Sitter universe the density contrast grows as the linear scale, so that the gravitational potential associated with the mass fluctuation is independent of time. Hence the red- and the blue-shift exactly compensate each other and the net effect is zero. However, a non-zero effect arises if the gravitational potential decays, as in the case of an open universe when the effect of the space curvature is important, or when the dynamics of the universe are dominated by dark energy.

As first pointed out by Crittenden & Turok (1996), a promising way of probing the ISW effect is through correlating fluctuations in the Cosmic Microwave Background (CMB) with large-scale structure. Since the timescale for the decay of the potential is of the order of the present-day Hubble time, the effect is largely canceled on small scales, because photons travel through multiple density peaks and troughs. This is why surveys covering large areas of the sky and probing the large scale distribution up to z ~ 1 are necessary.

A high quality all-sky CMB temperature map has been provided by the WMAP satellite (Bennett et al. 2003, Hinshaw et al. 2007, Hinshaw & Naeye 2008). A particularly well-suited probe of the large-scale structure is the NVSS survey, and indeed this has been extensively exploited to look for the ISW signal (Boughn & Crittenden 2004, Boughn & Crittenden 2005, Pietrobon et al. 2006, McEwen et al. 2007, McEwen et al. 2008, Ho et al. 2008, Giannantonio et al. 2008, Raccanelli et al. 2008).

The comparison of the correlations inferred from the data with model predictions requires once again the redshift distribution and the bias parameter as a function of redshift. All analyses carried out so far have used redshift distributions inconsistent with the CENSORS results. The product of the latter redshift distribution with the redshift-dependent bias factor best fitting the observed w() (see the previous sub-section), whose integral determines the amplitude of the ISW effect, peaks at redshifts where the contribution to the ISW signal in a CDM cosmology also peaks, namely z 0.4. This means that the NVSS sample is very well suited to test the effects of dark energy on the growth of structure. The predicted cross-correlation power spectrum between the surface density fluctuations of NVSS sources and the CMB fluctuations expected for the "concordance" CDM cosmology turns out to be in good agreement with the empirical determination using the CMB map obtained from WMAP data. This conclusion is at odds with that of Ho et al. (2008) who found that the WMAP 3-year model predicts an ISW amplitude about 2 below their estimate. Hence we suggest that the amplitude of the ISW cross-correlation does not support the case for new gravitational physics on cosmological scales (Afshordi et al. 2008) or for a large local primordial non-Gaussianity (Afshordi & Tolley 2008).