VIII. DETECTION SCHEMES

Detecting (or creating) dark matter is key in determining its properties and the role of dark matter in the formation of structure in the universe. Many experiments have searched and are currently searching for a signal of WIMP-like dark matter (many specifically for neutralinos) and each uses a different detection method. Although producing dark matter in a particle accelerator would be ideal (we would have better control and the experiment would be repeatable), but other methods to find dark matter, coined direct and indirect detection, also continue to be important in the search. Due to the summary nature of this article, only a brief overview of this large topic will be presented here. For a more thorough review of detection techniques and results, refer to L. Baudis and H. V. Klapdor-Kleingrothaus for direct detection and J. Carr et al. for indirect. [55, 56]

A. Production in Accelerators

Producing and detecting dark matter particles in an accelerator would be a huge step toward confirming the existence of dark matter (though it would not, intriguingly, verify that the produced particle acts as the vast amount of dark matter in the universe detected through astrophysical means). If we assume that R-parity is conserved and that the dark matter is the neutralino and thus the LSP, then a signal in an accelerator will have several distinctive features. When SUSY particles are created, they will decay to the LSP and most likely escape the detector (similar to a neutrino - remember SUSY particles interact very weakly with regular matter). As the LSP leaves the collision space, it will carry with it energy and momentum which can be detected as missing energy and momentum. Similar signatures of missing energy would be detected if the dark matter were Kaluza-Klein excitations or other exotic particles.

Although direct evidence for SUSY or other exotic particles hasn't been seen yet, there are certain processes which depend heavily on whether they exist. For example, the radiative quark decay process (s b) and the anomalous magnetic moment of the muon constrain the possible masses of SUSY particles. The constraints obtained from these and other experiments, however, are highly model dependent so it is therefore difficult to make any general claims about them. Since there is such uncertainty in the theory, we will generically refer in the following sections to dark matter particles as WIMPs (Weakly Interacting Massive Particles).

B. Direct Detection

The basic idea of direct detection is simple: set up a very sensitive device, containing a large amount of some element, which can detect very small motions and interactions of the atoms within it. If dark matter is everywhere in the universe, then it should be traveling around (and through) the earth, and therefore a detection apparatus, at all times. Although dark matter is weakly interacting, it may occasionally bump into the nucleus of a detector atom and deposit some energy which can be sensed by the detector. To get an idea of how much energy a WIMP would deposit, we first estimate that WIMPs are moving at velocities of about 220 km/s and their masses are somewhere around 100 GeV. We then crudely find a WIMP's kinetic energy using

(23)

This is the upper limit of energy that a 100 GeV neutralino traveling at 220 km/s could deposit in the detector; the actual amount would almost certainly be smaller, since it is unlikely for a weakly-interacting particle to be completely stopped within the detector. Natural radioactivity generally emits MeV energies, making a keV increase in energy due to nuclear scattering nearly impossible to find. For this reason, direct detection devices must be radioactively clean and shielded from particles that may make detection of WIMPs difficult.

The recoil energy E of a WIMP with mass m scattering off of a nucleus of mass M can be more precisely found with the expression

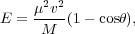(24)

where µ = mM / (m + M) is the reduced mass, v is the speed of the WIMP relative to the nucleus, and is the scattering angle.

A WIMP signal should have specific characteristics. First, events should be uniformly distributed throughout the detector given that the local dark matter density is thought to be fairly homogeneous and the cross section of interaction remains constant. Secondly, a WIMP-nucleus interaction should be a single-site event, whereas an event from cosmic rays or naturally occuring radioactivity can be multi-site. For this reason, detectors have an "anti-coincidence veto system" which makes sure events that occur extremely close together (within nanoseconds), suggesting that they are caused by the same incoming particle, are not counted as caused by other WIMPs. Detection rates should also vary at different times of the year due to the earth moving with or against the velocity of dark matter in the galaxy. This depends on the Earth's velocity, given by

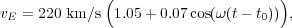(25)

where is 2/year and t₀ is June 2. As a result, the variation of WIMP flux over a year is only about 7%, meaning that many events would be required to see such a small modulation. These among other indications help detection experiments decide whether received signals really are WIMPs or not.

The interaction of a WIMP with the detector material can be classified by two characteristics: elastic or inelastic, and spin-dependent or spin-independent.

• Elastic and inelastic scattering: Elastic scattering is the interaction of a WIMP with the nucleus as a whole. This causes the nucleus to recoil and, as we have seen, would deposit energies of around 25 keV. In inelastic scattering all of the energy does not go into nuclear recoil; instead the nucleus is excited to a higher energy state (for example, the 5/2⁺ state in ⁷³Ge) which then decays by photon emission. If the excited state is long-lived enough, the decay signal can be separated from the nuclear recoil event; this leads to better background discrimination. However, inelastic scattering cross sections are generally smaller than elastic scattering cross sections due to a lack of coherence (the interaction is with individual nucleons rather than with the nucleus as a whole). [57]

• Spin-dependent and spin-independent scattering: Spin-dependent ("axial-vector") scattering results from the coupling of a WIMP's spin with the spin content of a nucleon. Spin-independent ("scalar") does not depend on this and has the advantage of higher cross sections with larger nuclei (because of coherence where the WIMP interacts with the nucleus as a whole).

A recoil event can then be further categorized, taking on one of three forms:

• Phonon/Thermal: A vibration (detected as a rise in temperature) in the crystal lattice of the detector, caused by the slight movement of a nucleus off which a WIMP has recoiled. An extremely sensitive thermometer system is located around the detector, allowing any temperature variation to be recorded.

• Ionization: An incident particle gives an electron in the detector enough energy to escape the pull of its nucleus. A small electric field is set up in the detector to "push" the new charge to a detector wall where it can be registered and counted as an ionization event.

• Scintillation: Caused when an electron absorbs enough energy to climb to a higher energy state. After a short time, the electron will lose this energy by emitting a photon, which is then gathered by photomultipliers and converted to an electric signal so it can be analyzed.

A detector is generally set up to sense two of these WIMP signals. By doing so, background events can be recognized on an event-by-event basis and discarded, allowing possible dark matter signatures to be counted and analyzed.

To calculate the number of recoil events N expected in a detector within a range of recoil energy (E₁, E₂), we take a sum over the nuclear species i in the detector:

(26)

where dR_i / dE is the expected recoil rate per unit mass of i per unit nucleus recoil energy and per unit time, and _i(E) is the effective exposure of i in the detector. dR_i / dE is given by

(27)

where is the local halo dark matter density, _i is the WIMP-nucleus cross section, F_i(E) is the nuclear form factor which takes into account that a nucleus is not a simple point particle, m is the WIMP mass, µ_i is the reduced mass, v is the velocity of the WIMP with respect to the detector, M_i is the mass of a nucleus of species i, E is the recoil energy, and f(, t) is the WIMP velocity distribution (generally assumed to be a Maxwell-Boltzmann distribution) in the reference frame of the detector. The nuclear physics uncertainties are locked into F_i(E) while the astrophysical uncertainties lie in the WIMP velocity distribution. _i(E) is given by

(28)

where is the total mass of nuclei of species i in the detector that has been active for a time T_i, and _i(E) is the counting efficiency for nuclear recoils of energy E.

We can see from these expressions that a detector should ideally have a large mass with which to receive signals, be operational for a long period of time, and be properly shielded against background radiation. An upper limit can be put on the WIMP-nucleus cross section by comparing expected events (using the above expressions) to observation. Any negative results from direct detection experiments are not wasted time and effort; instead, we can say that the WIMP does not exist in a certain tested area of the parameter space (for a given dark matter theory) and look toward more sensitive areas. Fortunately, experiments are reaching more advanced detection techniques and are approaching the parameter space in which WIMPs are believed to exist.

While many others are in operation worldwide, the three direct detection experiments which have yielded the best (most constrained) results for the spin-independent WIMP-nucleus cross section are the Cryogenic Dark Matter Search (CDMS II) in the Soudan Mine, the UK Dark Matter Collaboration's ZEPLIN-I (ZonEd Proportional scintillation in LIquid Noble gases) in the Boulby Mine, and XENON10 at the Gran Sasso Underground Laboratory.

Each of these three collaborations uses a different method to look for WIMPs. CDMS II uses a set of 250 gram Ge detectors and 100 gram Si detectors cooled to less than 50 mK. Each apparatus is classified as a ZIP (Z-dependent Ionization and Phonon) detector. While WIMPs recoil off of nuclei, background particles scatter off of electrons; the ZIP detectors are able to discriminate between the two events. [58] ZEPLIN-III uses the scintillation properties of liquid Xe to detect WIMPs, shielded by lead and a liquid scintillator veto to reduce background radiation. [59] XENON10 also uses liquid Xe to detect scintillation and ionization events. [60] The exclusion curves from these collaborations are shown in Fig. (6).

Figure 6. Spin Independent cross section versus WIMP mass with exclusion curves. The blue(top shaded) area is the DAMA claimed discovery region. The remaining shaded areas are regions of parameter space in which theory predicts dark matter candidates. The exclusion curves are: dashed - ZEPLIN III, solid line - CDMS II, dotted line - XENON 10. Models above the exclusion curves are experimentally ruled out. This plot was produced with the Dark Matter Limit Plot Generator.

One experiment, the DAMA collaboration, detected an annual modulation in scattering events that is around the expected 7%. [61] This is puzzling, however, because no other direct detection experiment has found such a signal. P. Gondolo and G. Gelmini have given possible reasons for this; for example, the WIMP velocity may be larger than the DAMA thresholds, but smaller than the thresholds of other detectors. [62] However, DAMA's conclusions still remain controversial.

Other collaborations focusing on spin-independent direct detection include CRESST and EDELWEISS. [63, 64] Many other future projects have been proposed, such as GENIUS and SuperCDMS, which is planned to be able to probe nearly all split-supersymmetry model parameter space. [65, 66]

Although spin-independent scattering has larger interaction rates in most SUSY models, spin-dependent scattering can explore the parameter space where scalar interaction is less probable. For this reason, experiments searching for spin-dependent interactions have been able to set competitive upper limits on WIMP interactions. For example, ⁷³Ge makes up 7.73% of the CDMS Collaboration's natural germanium detectors, and ²⁹Si accounts for 4.68% of the natural silicon, both which have nonzero spin. As a result, CMDS's spin-dependent experiments have placed the best current upper limit on WIMP-neutron interactions. [67] Other direct detection experiments employing spin-dependent techniques include PICASSO and NAIAD. [68, 69]

C. Indirect Detection

In supersymmetry, for example, neutralinos are classified as Majorana particles (they are their own antiparticle) and therefore annihilate with each other, giving off various products which we can detect. Hence a potential signal for the existence of dark matter is WIMP-WIMP annihilation. This technique is called "indirect detection" since we are not actually detecting the WIMPs themselves. Because the annihilation rate of WIMPs is proportional to the square of the dark matter density (_{A dm}²), natural places to look for dark matter annihilations are those expected to have high WIMP densities, such as the sun, earth, and galactic center. Annihilation products include gamma-rays, neutrinos, and antimatter.

1. Gamma-rays

Gamma-rays from WIMP annihilation are believed to occur most frequently in the galactic center. One way this process can take place is through a WIMP annihilation yielding a quark and anti-quark, which then produce a particle jet from which a spectrum of gamma-rays is released. The quark anti-quark fragmentation process has been thoroughly studied at accelerators and is well understood; the creation and propagation of gamma rays from such a jet is a fairly predictable process (compared to, for example, the "random walk" of charged antimatter particles through space). A second form of gamma-ray production is the decay of WIMPs directly to gamma-rays, or Z), which produces gamma-rays (a "gamma-ray line") that are proportional to the mass of the WIMPs involved. Since typcial WIMP masses can be on the order of 100s of GeV, these are extremely high energy gamma rays. Although the flux is small and quite difficult to detect, observing such a gamma-ray line would be an obvious indication for dark matter annihilation and the WIMP mass (often referred to as the "smoking gun").

As a gamma-ray enters an indirect detection device, it first passes through an anti-coincidence shield which limits the amount of charged particles entering the detector. The gamma-ray then encounters "conversion foils," which are thin sheets of heavy nuclei that convert the photon to a e⁺ e^- pair. A calorimeter tracks the energies of the positron and electron, while particle tracking detectors measure their trajectories. The signature of a gamma-ray event is then a registered energy with nothing triggering the anti-coincidence shield, and the indication of two particles (the positron and electron) coming from the same location.

The EGRET Collaboration reported an excess of gamma-rays in 1998, pointing toward already accepted characteristics of dark matter: a 50-70 GeV WIMP mass and a ring of concentrated dark matter at a radius of 14 kpc from the galactic center (which would nicely answer for our flat rotation curves). [70] This discovery is initially encouraging, but as Bergström et al. have shown, observed antiproton fluxes would have to be much larger if these excess gamma rays are being produced by neutralino or generic WIMP self annihilation. [71] For this reason and others, EGRET's results remain controversial.

2. Neutrinos

Neutrinos can be another important product of WIMP annihilation. As WIMPs travel through the universe and through matter, they lose small amounts of energy due to scattering off of nuclei. Therefore, WIMPs can gather at the centers of large gravitating bodies, increasing their density until their annihilation rate equals half the capture rate (two WIMPs are needed for annihilation, where only one is needed for capture). For many of the primary particle physics models, the WIMP annihilation and capture rates are at (or nearly at) equilibrium in the sun, a conveniently "close" object to observe. This equilibrium should allow for a steady annihilation rate, and therefore a constant flow of neutrinos emanating from within the sun (we study only the neutrinos and not other products of annihilation because neutrinos interact so weakly that most escape from the sun or body in question). Why not, then, study neutrinos coming from WIMP annihilations within the earth, an even closer gravitating body? The earth (in most models) has not reached such an equilibrium and thus does not provide a flux of neutrinos; it is less massive than the sun, so it causes less WIMP scattering and a much smaller gravitational potential well. Neutrino telescopes therefore usually focus on neutrino flux coming from the sun, rather than the earth.

Depending on the WIMP's mass and composition, annihilation processes include t , b , c 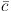, ZZ, W⁺ W^-, and ^{+ -}, which then decay to neutrinos among other products. For neutralinos or generic WIMPs lighter than W^±, annihilation to b 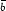and ^{+ -} are the most common processes, yielding neutrinos with energies around 30 GeV. WIMPs with higher masses annihilate to Higgs and gauge bosons, top and bottom quarks, and muons, leading to neutrinos of masses that are much easier to detect (about half of the WIMP mass). Detection, then, depends heavily on the WIMP mass, as well as the annihilation rate, density within the sun, and other factors.

As neutrinos pass through the earth, they sometimes interact with the hydrogen and oxygen and other atoms around the optical modules of a neutrino detector. Electrons, muons, and taus produced by such events are extremely energetic and are traveling faster than the speed of light in the medium; the particles are then detected optically due to the Cherenkov radiation they emit. The expected number of observed muons N can be found using

(29)

where A is the area of the detector and P_{v µ} represents the combined probabilities that a neutrino will interact in the volume viewed by the optical modules, and that the muon can travel far enough for it to be detected.

Because neutrinos are so weakly interacting, neutrino telescopes must be massive to detect a significant signal. AMANDA-II is a neutrino detector 1500 to 2000 meters underground within the ice of the South Pole where Cherenkov radiation can travel and be seen easily by optical modules. This experiment has not detected statistically significant results from the direction of the sun, but has placed helped place firm limits on the muon flux. [73] A future experiment (expected to be fully completed in 2011), IceCube, will integrate AMANDA into a much larger detection experiment, with 7200 optical modules and a detector volume of a cubic kilometer. [74] Super-Kamiokande ("Super-K") is another indirect detection experiment, located underground in the Kamioka-Mozumi mine in Japan. The detector consists of 50,000 tons of water and detects Cherenkov radiation from incoming muons as well. Super-K looks in the direction of the sun, earth, and galactic center, and, like AMANDA, has not detected any excess of muon rates above the expected background. [75]

3. Antimatter

Antimatter can be a excellent signal of WIMP annihilation precisely because antimatter is relatively rare cosmically, and many of the astrophysical processes which create antimatter are well understood. For example, the annihilation of WIMPs can also produce antiprotons via q through hadronization (where the dominate annihilation process yields b quarks and antiquarks), and positrons through secondary products of the annihilation such as W⁺ W^- (and ZZ), where W (or Z) e⁺ v_e. Unlike gamma-rays and neutrinos, these products are charged and thus affected by magnetic fields within space and also lose energy due to inverse Compton and synchrotron processes, so we cannot make any conclusions about where the annihilations occurred. We therefore study the flux of antimatter particles from the galactic halo as a whole, rather than assumed dense areas such as the galactic center or large bodies.

Experiments searching for antimatter must be located near the top of the earth's atmosphere; various other cosmic rays and their consequential particle showers create too large and uncertain of a background to make conclusive analyses. It is important, however, to still consider and subtract any background caused by cosmic rays that reach the edges of our atmosphere. In 1994, the HEAT Collaboration detected an excess of cosmic ray positrons of energies around 10 GeV possibly caused by neutralino self-annihilation, and confirmed this signal again in 2000. [76, 77] A "boost factor," however, must be applied to the WIMP annihilation rate of a smooth halo in order to match the HEAT data; this is perhaps an indication that we exist within an extremely clumpy halo, or that there are other unknown sources of antimatter. The Balloon-borne Experiment with Superconducting Spectrometer (BESS) also detected antiprotons with energies up to 4 GeV during its nine flights over several years. [78]

Quite recently, the results from the PAMELA (a Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics) satellite-borne experiment's flight from July 2006-February 2008 were released. The collaboration found that the positron fraction increases sharply over much of the range of 1.5-100 GeV and thus concluded that a primary source, either an astrophysical object or dark matter annihilation, must be present to account for the abundance of cosmic-ray positrons. [79] The data from PAMELA also require heavy WIMP candidates or large boost factors associated with non-uniform clumps in the dark matter distribution, thus constraining the nature of the possible dark matter. ATIC (Advanced Thin Ionization Calorimeter), a balloon-based experiment, also reported an excess of e^- or e⁺ at 300-800 GeV. However, recent results from Fermi [81] and HESS [82] (the High Energy Stereoscopic System, a set of four Cherenkov telescopes in Namibia) do not see the same electron-positron excess of ATIC leaving the issue far from settled (however, Fermi does see an excess similar to that seen by PAMELA). Further data is necessary to determine if excess gamma ray and antimatter fluxes are indeed signals of dark matter annihilation or signatures of local astrophysical objects and backgrounds.