Annu. Rev. Astron. Astrophys. 2004. 42: 603-683 Copyright © 2004 by Annual Reviews. All rights reserved

2. SECULAR EVOLUTION OF BARRED GALAXIES

We see only snapshots of galaxy evolution, so it is difficult to study slow processes. ¹ Why do we think that secular evolution is happening? We begin with an existence proof - a review of how n-body simulations account for the morphological features seen in barred galaxies. Our suggestion that pseudobulges are constructed out of rearranged disk gas is embedded in this larger picture of SB secular evolution.

2.1. Morphology of Barred Galaxies

Barred galaxies are reviewed in detail by Sellwood & Wilkinson (1993). Their morphology is discussed by de Vaucouleurs (1959, 1963), Sandage (1961, 1975), Kormendy (1979b), Sandage & Bedke (1994), Buta & Crocker (1991), Buta & Combes (1996), and Buta (1995, 1999). We use these diagnostic features:

1. Barred spiral galaxies are divided into subclasses SB(s), in which the spiral arms begin at the ends of the bar, and SB(r), in which a complete inner ring of stars connects the ends of the bar. In the latter case, the spiral arms start somewhere on the ring, "often downstream from the ends of the bar" (Sandage & Bedke 1994). SB(r) and SB(s) galaxies are contrasted in Figure 6; additional SB(r) galaxies are shown in Figure 3 and Figure 5, and additional SB(s) galaxies are shown in Figure 7.

2. Some barred and oval galaxies have outer rings (R) that are 2.2 ± 0.1 times the diameter of the bar or inner disk. Outer rings in barred and unbarred galaxies are similar [Figure 2 and Figure 5]. Inner and outer rings are different; there is no size overlap. Some galaxies contain both (Figure 5).

3. At intermediate Hubble types, when the bar is made mostly of old stars and the disk contains many young stars, the stellar population of inner and outer rings is like that of the disk, not like that of the bar (Figures 2 and 3). Inner and outer rings generally contain gas.

4. In SB(s) galaxies, an almost-straight dust lane parallels the ridge line of the bar but is displaced slightly forward in the direction of galactic rotation. Such dust lanes are analogous to and connect up with the prominent dust lanes seen on the trailing side of the arms in global-pattern spirals. Examples are shown in Figure 6 and in Figures 7 and 8. These dust lanes are almost never present in SB(r) galaxies (Sandage 1961). NGC 1512 in Figure 3 is a rare exception.

5. Many barred and oval galaxies have very active star formation near their centers, in what is conventionally identified as the bulge. Often the star formation is concentrated in a ring. Figures 3, 7, and 8 show examples.

6. Many barred galaxies have pseudobulges that are elongated into a structure resembling a bar. Examples are shown in Figure 14.

7. Many early-type SB galaxies contain a lens in the disk - a shelf of slowly decreasing surface brightness with a sharp outer edge. Lenses have intrinsic axial ratios of ~ 0.85; the bar usually fills the longest dimension. These properties are discussed in Kormendy (1979a, b, 1981, 1982a) and in Athanassoula et al. (1982). Lenses are sometimes seen in unbarred galaxies; NGC 1553 is the best example (Freeman 1975, Kormendy 1984). Lenses in early-type galaxies look similar to oval disks in late-type galaxies (Section 3.2); it is not clear whether or not they are physically similar. Lenses are illustrated in Figures 2 and 5.

Figure 2. Prototypical outer rings in barred and unbarred galaxies. NGC 1291 is an (R)SB(lens)0/a galaxy - it has a bar embedded in a lens of the same major-axis diameter (see also Kormendy 1979b). NGC 4736 is classified (R)SA(r)ab. This figure shows how blue the outer rings are: They are dominated by young stars. Both rings also contain H I gas (van Driel et al. 1988, Bosma et al. 1977b). Sources: NGC 1291 (Buta, Corwin, & Odewahn 2003); NGC 4736 (NOAO).

Figure 3. NGC 1512, an SB(r)ab galaxy imaged with HST by Maoz et al. (2001). This figure (courtesy NASA and ESA) illustrates the stellar population of inner rings. As is common in intermediate-Hubble-type galaxies, the bar in NGC 1512 is made of old, red stars and the disk is made of young, blue stars. This figure shows that the inner ring has the same stellar population as the disk, not the bar. Also seen at center is a nuclear star-formation ring that is shown at higher magnification in Figure 8 and the start of a well-developed, curved dust lane (cf. Figures 6-8) that extends out of the field of view to the right. The corresponding dust lane on the other side is visible near the central ring but not at larger radii. The outer parts of NGC 1512 are illustrated by Sandage & Bedke (1994), who note that NGC 1512 is morphologically normal except for some distortion of its outer spiral structure (not shown here) by a tidal encounter with neighboring NGC 1510.

2.2.Dynamics of Barred Galaxies: The Importance of Resonances

To understand bar-driven evolution, we need to dip briefly into the dynamics of bars. An in-depth review is provided by Sellwood & Wilkinson (1993). Here we need a primer on the nature and importance of orbital resonances.

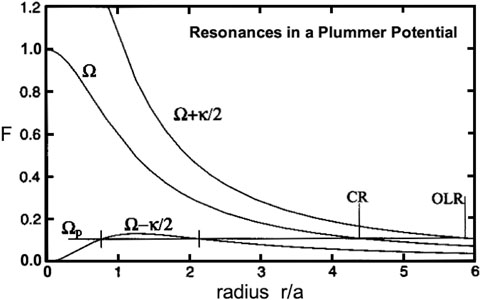
Seen from an inertial frame, an orbit in a galactic disk is an unclosed rosette. That is, there are a nonintegral number of radial oscillations for every revolution around the center. However, in a frame of reference that rotates at the average angular velocity of the star, the star's mean position is fixed, and its radial oscillation makes it move in a small ellipse around that mean position. ² Any global density pattern such as a bar that rotates at the above angular velocity will pull gravitationally on the star in essentially the same way at all times and will therefore make large perturbations in its orbit. Corotation is the strongest of a series of resonances in which the pattern repeatedly sees the star in the same way.

For example, there is another rotating frame in which the star executes two radial oscillations for each circuit around the center. If a bar rotates at this angular velocity, it sees the stellar orbit as closed, roughly elliptical, and centered on the galactic center (Figure 4). This is called inner Lindblad resonance (ILR). It occurs when the pattern speed of the bar is _p = - /2, where is the average angular velocity of revolution of the star and is its frequency of radial oscillation. The limit of small radial oscillations is called the epicyclic approximation; then ² = (2V / r)(V / r + dV / dr), where V(r) is the circular-orbit rotation curve (Mihalas & Routly 1968 provide a particularly transparent discussion).

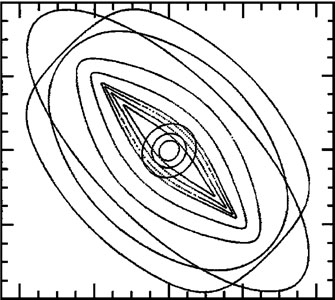Figure 4. (Top) Frequencies (r) = V(r) / r and ± /2, where 2 = (2V / r) (V / r + dV / dr) is the epicyclic frequency of radial oscillations for almost circular orbits. This figure (Sparke & Gallagher 2000) is for a Plummer potential, but the behavior is generic. For a pattern speed p, the most important resonances occur where p = (corotation), p = + /2 [outer Lindblad resonance (OLR)], and p = - /2 [two inner Lindblad resonances (ILR), marked with vertical dashes]. (Bottom) From Englmaier & Gerhard (1997), examples of the principal orbit families for a bar oriented at 45° as in Figure 7. The elongated orbits parallel to the bar are the x1 family out of which the bar is construc ted. Interior to ILR (or outer ILR, if there are two LRs), the x2 family is perpendicular to the bar. Near corotation is the 4:1 ultraharmonic resonance; the almost-square orbit makes four radial oscillations during each circuit around the center. Since the principal orbits change orientation by 90° at each resonance shown, they must cross near the resonances.

Resonances are important for several reasons. Figure 4 shows generic frequency curves and the most important periodic orbit families in a barred galaxy. We can begin to understand how a self-consistent bar is constructed by exploiting the fact that - /2 varies only slowly with radius (except near the center, if there is an ILR). Calculations of orbits in a barred potential show that the main family of orbits (called x₁) is elongated parallel to the bar between ILR and corotation. Bars are largely made of x₁ orbits and similar, nonperiodic orbits that are trapped around them by the bar's self-gravity. Typical x₁ orbits are shown in the bottom panel of Figure 4. They are not nearly circular, but the essence of their behavior is captured if we retain the language of the epicyclic approximation and say that orbits of different radii look closed in frames that rotate at different angular velocities - /2. But if - /2 varies only a little with radius, then it is possible to pick a single pattern speed _p in which the orbits precess almost together. If they precessed exactly together, then one could make a bar by aligning elongated orbits as in the bottom panel of the figure. Because - /2 is not quite constant, it is the job of self-gravity to make the orbits precess not approximately but exactly together. This idea was used to understand self-consistent bars by Lynden-Bell & Kalnajs (1972) and by Lynden-Bell (1979) and to demystify spiral structure by Kalnajs (1973) and by Toomre (1977b). They were following in the pioneering footsteps of Bertil Lindblad (1958; see section 20 of Lindbald 1959).

Calculations of orbits in barred potentials reveal other orbit families (e.g., Contopolous & Mertzanides 1977; Athanassoula 1992a, b; Sellwood & Wilkinson 1993), only a few of which are relevant here. Next in importance is the x₂ family, which lives interior to ILR and which is oriented perpendicular to the bar (Figure 4, bottom). Between corotation and OLR, the principal orbits are elongated perpendicular to the bar, and outside OLR, they are again oriented parallel to the bar. Near corotation is the 4:1 ultraharmonic resonance in which a star executes 4 radial oscillations for every revolution: _p = - /4. We need these results in the following sections.

The important consequence is emphasized by Sellwood & Wilkinson (1993): "Not only do the eccentricities of the orbits increase as exact resonance is approached, but the major axes switch orientation across all three principal resonances, making the crossing of orbits from opposite sides of a resonance inevitable" (bottom panel of Figure 4). This is important mainly when the orbits are very noncircular, as they are in strongly barred galaxies. Now, orbits that cross are no problem for stars. But gas clouds that move on such orbits must collide near resonances. Dissipation is inevitable; the consequence is an increase in the gas density and star formation. This heuristic discussion helps to explain the numerical results reviewed in the following sections, in which gas tends to build up in rings and to form stars there.

2.3. Bar-Driven Radial Transport of Gas: The Formation of Rings

Theory (Binney & Tremaine 1987; Sellwood & Wilkinson 1993; Lynden-Bell 1979, 1996) and n-body simulations (Sellwood 1981, Sparke & Sellwood 1987, Pfenniger & Friedli 1991, Athanassoula 2003) show that bars grow by transferring angular momentum to the outer disk, thereby driving spiral structure. As a result, stellar orbits in the bar get more elongated, and the bar grows in amplitude. Its pattern speed slows down.

The essence of the response of gas to a bar is captured in figure 3 of Simkin, Su & Schwarz (1980), reproduced here as Figure 5. Outside corotation, gas is driven outward by the angular momentum transfer from bar to disk that makes the bar grow. This gas collects into an outer ring near OLR. As discussed earlier, outer rings are oriented perpendicular to the bar when they are interior to OLR; this is the usual situation (Kormendy 1979b, Buta 1995). At radii well inside corotation, gas falls toward the center. This is the gas that is believed to make pseudobulges. Within an annular region around corotation, gas is collected into an inner ring near corotation or near the 4:1 ultraharmonic resonance.

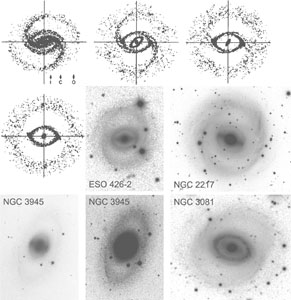Figure 5. Evolution of gas in a rotating oval potential (Simkin, Su, & Schwarz 1980; see also Schwarz 1981, 1984). The gas particles in this sticky-particle n-body model are shown after 2, 3, 5, and 7 bar rotations (top-left through center-left). Arrows show the radii of ILR, corotation, and OLR. Four SB0 or SB0/a galaxies are shown that have outer rings and a lens (NGC 3945) or an inner ring (obvious in ESO 426-2 and in NGC 3081, but poorly developed in NGC 2217). Sources: NGC 3945 (Kormendy 1979b); NGC 2217, NGC 3081 (Buta et al. 2003); ESO 426-2 (Buta & Crocker 1991).

This behavior is seen in a variety of simulations starting as early as Prendergast (1964), Duus & Freeman (1975), and Sørensen et al. (1976). By the early 1980s, there was already an extensive literature on the subject (see Kormendy 1982a and Prendergast 1983 for reviews).

The reason why SB(r) and SB(s) galaxies are different was investigated by Sanders & Tubbs (1980). They simulated the response of gas to an imposed, rigid bar potential that they grew inside a disk galaxy. Examples of the steady-state gas response are shown in Figure 6. In the top two rows of panels, the strength of the bar increases from left to right, either because the ratio of bar mass to disk mass increases (top row), or because the bar gets more elongated (second row). In both cases, weak bars tend to produce an SB(s) response, while strong bars produce ring-like structures that resemble SB(r) galaxies. If the bar gets too strong (top-right panel), the result does not look like a real galaxy. The bottom row of simulations explores the effect of varying the bar's pattern speed. Rapid pattern speeds produce dramatically SB(s) structure. Slower pattern speeds in which corotation is near the end of the bar produce inner rings. Very slow pattern rotation (right panel, in which corotation is at 3 bar radii) produce responses that do not look like real galaxies. This is because _p is now so small that the radius of ILR is large. Inside ILR, closed gas orbits align perpendicular to the bar. These can never have substantially the same radius as the bar, as they do in the bottom-right simulation in Figure 6. If the response to the bar were perpendicular to the bar over most of the radius of the bar, it would be impossible to make that response add up to a self-consistent bar. Pattern speeds are never so slow that corotation radii are so far out in the disk that the entire bar is inside ILR. This was possible in Sanders & Tubbs (1980) only because the bar was inserted by hand and given a chosen (not a self-consistent) pattern speed. Theoretical arguments tell us that bars end inside or near corotation (Contopoulos 1980, Sellwood & Wilkinson 1993). Observations agree (Kent 1987b; Merrifield & Kuijken 1995; Gerssen, Kuijken & Merrifield 1999, 2003; Debattista & Williams 2001; Debattista, Corsini & Aguerri 2002; Aguerri, Debattista & Corsini 2003; Corsini, Debattista & Aguerri 2003; see Elmegreen 1996 for a review) except in late-type galaxies in which V r rotation curves imply that the bar is safely clear of ILR anyway (Elmegreen 1996; Elmegreen, Wilcots & Pisano 1998).

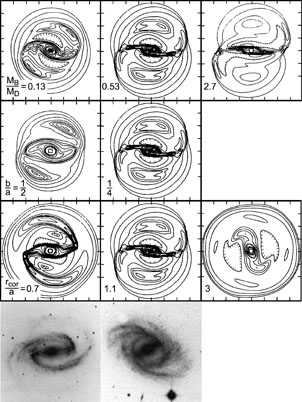Figure 6. Contours of steady-state gas density in response to a bar (adapted from Sanders & Tubbs 1980, who also show intermediate cases). The bar is horizontal and has a length equal to four axis tick marks. The top row explores the effect of varying the ratio MB / MD of bar mass to disk mass. The second row varies the bar's axial ratio b / a. The third row varies the bar pattern speed, parameterized by the ratio rcor / a of the corotation radius to the disk scale length. The middle column is the same standard model in each row; it approximates an SB(r) galaxy such as NGC 2523 (bottom center). The left panels resemble SB(s) galaxies such as NGC 1300 (bottom left). The right panels carry the parameter sequences to unrealistic extremes; they do not resemble real galaxies.

Despite the above successes, Sanders & Tubbs (1980) share a number of technical problems with other early simulations of gas response to bars. Their beam scheme (Sanders & Prendergast 1974) code has coarse spatial resolution and unphysical numerical viscosity (see Athanassoula 1992b and Sellwood & Wilkinson 1993). In fact, there are conflicting views on whether viscosity is important at all; Combes (1998) suggests that it is negligible compared with gravitational torques, whereas Sellwood & Wilkinson (1993) at least consider the possibility that it is important. Gas infall timescales are very uncertain in early simulations.

Still, the main conclusion reached by Sanders & Tubbs (1980) - that weak, fast bars favor SB(s) structure and that strong, slow bars favor SB(r) structure - has largely been confirmed by higher-quality simulations (e.g., Schwarz 1984, Byrd et al. 1994, Salo et al. 1999). Well-motivated hints of these results came much earlier (Freeman 1970b). Therefore a widespread feeling has developed that we understand the essentials of ring formation.

Nearly radial dust lanes in bars (see Section 2.1 and Figures 3, 6, 7, 8) are a particularly important diagnostic of SB evolution. They are widely believed to be the observational signatures of shocks that drive gas infall. The idea was proposed by Prendergast (1964); other early studies include Sørensen, Matsuda, & Fujimoto (1976); Roberts, Huntley, & van Albada (1979), and, as discussed above, Sanders & Tubbs (1980).

Figure 7. Comparison of the gas response to a bar (model 001 by Athanassoula 1992b) with NGC 5236 (left) and NGC 1365 (right). The galaxy images were taken with the VLT and are reproduced courtesy of ESO. In the models, the bar potential is oriented at 45° to the horizontal, parallel to the bar in NGC 5236. The bar axial ratio is 0.4, and its length is approximately half of the box diagonal. The top-right panel shows the velocity field; arrow lengths are proportional to flow velocities. Discontinuities in gas velocity indicate the presence of shocks; these are where the gas density is high in the density map at top left. High gas densities are identified with dust lanes in the galaxies. The model correctly reproduces the observations that (a) dust lanes are offset in the forward (rotation) direction from the ridge line of the bar; (b) they are offset by larger amounts nearer the center; and (c) very near the center, they curve and become nearly azimuthal. As emphasized by the velocity field, the shocks in the model and the dust lanes in the galaxy are signs that the gas loses energy. Therefore it must fall toward the center. In fact, both galaxies have high gas densities and active star formation in their bright centers (e.g., Crosthwaite et al. 2002; Curran et al. 2001a, b).

Figure 8. Nuclear star-formation rings in barred and oval galaxies. For NGC 4314, a wide-field view is at top left; for NGC 4736, the wide-field view is as in Figure 2. Sources: NGC 4314 (Benedict et al. 2002); NGC 4736 (NOAO); NGC 1326 [Buta et al. 2000 and Zolt Levay (STScI)]; NGC 1512 (Maoz et al. 2001); NGC 6782 (Windhorst et al. 2002 and the Hubble Heritage Program).

In an important paper, Athanassoula (1992b) explored the response of inviscid gas to a bar using a high-resolution code. Her main focus was gas shocks and their relation to dust lanes. Typical results are shown in Figure 7. If the mass distribution is centrally concentrated enough to result in an ILR, then the dust lanes are offset in the forward (rotation) direction from the ridge line of the bar. Because of the presence of the x₂ orbits - the ones that align perpendicular to the bar inside ILR - the offset is largest near the center (Figure 7). The models reproduce the observation that the dust lanes in many bars curve around the center of the galaxy at small radii and become nearly azimuthal. Athanassoula found that the dust lanes are more curved into an open S shape when the bar is weak; this is confirmed observationally by Knapen, Pérez-Ramírez, & Laine (2002) and is illustrated for NGC 6782 in Figure 8. As Athanassoula notes, "the resemblance between [the models and the observations] is striking."

The important consequence of this work is that shocks inevitably imply that gas flows toward the center. Because the shocks are nearly radial, gas impacts them at a steep angle. Therefore much of the velocity that is lost in the shock is azimuthal. This robs the gas of energy and forces it to fall toward the center.

Athanassoula estimated that azimuthally averaged gas sinking rates are typically 1 km s^-1 and in extreme cases up to ~ 6 km s^-1. Viscosity is not an issue in her models, so these estimates are more realistic than earlier ones. Because 1 km s^-1 = 1 kpc (10⁹ yr)^-1, the implication is that most gas in the inner part of the disk - depleted by star formation but augmented by mass loss during stellar evolution - finds its way to the vicinity of the center over the course of several billion years, if the bar lives that long.

In recent years, simulations have continued to concentrate on these inner regions of barred galaxies where dust lanes and star formation are most important (Friedli & Benz 1993, 1995; Piner, Stone & Teuben 1995; Englmaier & Gerhard 1997; Salo et al. 1999; Weiner, Sellwood & Williams 2001a; Regan & Teuben 2003). The conclusions are as follows: (a) Gas flows toward the center. (b) Star formation fed by the inflow is often concentrated in a narrow nuclear ring. (c) The inflow is a result of gravitational torques produced by the bar, but its immediate cause is the shocks. In essence, these are produced because gas accelerates as it approaches and decelerates as it leaves the potential minimum of the bar. So it tends to pile up near the ridge line of the bar. Incoming gas overshoots a little before it plows into the departing gas, so the shocks are nearly radial but offset from the ridge line of the bar in the forward (rotation) direction. The above simulations confirm Athanassoula's conclusion that offsets happen when the central mass concentration is large enough to allow a "sufficient" range of x₂ orbits. The agreement in morphology between the simulated shocks and the observed dust lanes has continued to improve. But there is an even better reason to think that they are connected. Compelling support is provided by the observation of large velocity jumps across the dust lanes (Pence & Blackman 1984; Lindblad, Lindblad & Athanassoula 1996; Regan, Sheth & Vogel 1999; Weiner et al. 2001b; and especially Regan, Vogel & Teuben 1997).

What happens to the infalling gas? Star formation is almost inevitable. The simulations, expectations from the Schmidt (1959) law, observations of young stars in SB nuclei, and star-formation indicators (Section 5) all point to enhanced star formation, often in substantial starbursts near the center. Examples are shown in Figure 8. NGC 4314 is a barred galaxy whose central star formation is also illustrated in the Hubble Atlas (Sandage 1961). NGC 1512 is an SB(rs) galaxy whose outer parts are shown in Figure 2. The dust lane in the bar is best seen in the Carnegie Atlas of Galaxies (Sandage & Bedke 1994). NGC 6782 contains an oval disk with an embedded bar. Finally, NGC 4736 is a prototypical unbarred oval galaxy. It is included to illustrate the theme of the next section, namely that barred and oval galaxies evolve similarly.

The examples shown in Figure 8 all have star formation concentrated in tiny rings with mean radii ~ 0.5 kpc (Buta & Crocker 1993). The physics that determines their radii is complicated and not well understood. It is likely that inflow physics and star-formation physics are both involved. In any case, nuclear star formation rings are quite common; the most prominent examples have been known for a long time (Morgan 1958; Burbidge & Burbidge 1960, 1962; Sandage 1961; Sérsic & Pastoriza 1965, 1967). Kennicutt (1994, 1998a) has reviewed the data, contrasting the global star formation in barred galaxies, which is indistinguishable from that in unbarred galaxies, with the nuclear star formation, which is enhanced over that in unbarred galaxies. As is predicted by simulations, there is plenty of fuel - the central concentration of molecular gas is higher in barred than in unbarred galaxies (Sakamoto et al. 1999). Additional examples of nuclear star-formation rings - and multiple discussions of the best cases - can be found in van der Kruit (1976); Rubin, Ford & Peterson (1975); Hummel, van der Hulst & Keel (1987); Gerin, Nakai & Combes (1988); Benedict et al. (1993, 1996, 2002); Buta (1986a, b, 1988, 1995); Pogge (1989); García-Barreto et al. (1991); Devereux, Kenney & Young (1992); Buta & Crocker (1993); Buta & Combes (1996); Maoz et al. (1996); Elmegreen et al. (1997); Colina et al. (1997); Buta & Purcell (1998); Martini & Pogge (1999); Buta et al. (2000); Pérez-Ramírez et al. (2000); Wong & Blitz (2000); Waller et al. (2001); Knapen, Pérez-Ramírez & Laine (2002); Erwin & Sparke (2003); Eskridge et al. (2003); Martini et al. (2003); and Fathi et al. (2003).

Many of the galaxies discussed in the above papers are barred. Those that are classified as transition objects (SAB) or as unbarred (SA), have created some uncertainty about how much the star formation depends on bars. However, many SAB and some SA objects are prototypical oval galaxies such as NGC 2903, NGC 3504, NGC 4736 (Figures 2 and 8), NGC 5248, and NGC 6951 (see Sandage 1961). We show in Section 3.3 that barred and oval galaxies are essentially equivalent as regards gas inflow, star formation, and pseudobulge building. Section 3.4 suggests that similar evolution happens in unbarred spirals that do not have an ILR.

We argue in later sections, as did some of the above authors, that the nuclear star formation is building pseudobulges. Although the star formation is frequently in a ring, it is not likely to form a ring of stars. If the star-forming ring is associated with ILR, then its radius should change as the central concentration of the galaxy evolves. We expect that the ring of star formation burns its way through the pseudobulge as it grows. Also, the spiral dust lanes interior to the star-formation rings (Figure 8) suggest that gas continues to sink inside ILR (Elmegreen et al. 1998). Finally, we choose to illustrate star-forming rings, because they most clearly establish the connection between star formation and bar-driven secular evolution. However, in many galaxies, the star formation is spread throughout the central region. An example is NGC 1365 (Figure 7; Knapen et al. 1995a, b; Sakamoto et al. 1995; Lindblad 1999).

In summary, a comprehensive picture of the secular evolution of barred galaxies has emerged as simulations of gas response to bars have succeeded with increasing sophistication in matching observations of galaxies. Bars rearrange disk gas to make outer rings, inner rings, and central mass concentrations. SB(s) structure is favored if the bar is weak or rotating rapidly; SB(r) structure is favored if the bar is strong or rotating slowly. Because bars grow stronger and slow down as a result of angular momentum transport to the disk, we conclude that SB(r) galaxies are more mature than SB(s) galaxies. Consistent with this, dust lanes diagnostic of gas inflow are seen in SB(s) galaxies but only rarely in SB(r) galaxies. By the time an inner ring is well developed, the gas inside it has been depleted. Embedded in this larger picture is the most robust conclusion of both the modeling and the observations - that a substantial fraction of the disk gas falls down to small galactocentric radii in not more than a few billion years. Star formation is the expected result, and star formation plausibly associated with bars (concentrated near resonance rings) is seen. These results provide part of the motivation for our conclusion that secular evolution builds pseudobulges.

¹ Mergers are an easier problem - transient phenomena such as tidal tails are readily recognizable (Toomre & Toomre 1972, Schweizer 1990). Back.

² It is an ellipse and not just radial motion because the star revolves faster than average near pericenter and slower than average near apocenter. Back.