1. INTRODUCTION: THE KENNICUTT-SCHMIDT LAW OF STAR FORMATION

Star formation and stellar evolution are such important drivers of galactic evolution that empirical laws to determine the star formation rate have been investigated for over 50 years. The results have never been very precise because star formation spans a wide range of scales, from cluster-forming cores to molecular clouds to the whole interstellar medium.

On the scale of a galaxy, the first idea was a proposed connection between the total star formation rate and the mass of interstellar gas. Schmidt (1959) derived the star formation rate (SFR) over the history of the Milky Way assuming a constant initial luminosity function for stars, (M_V), a stellar lifetime function T(M_V), a gas return per star equal to all of the stellar mass above 0.7 M, and a star formation rate f(t) that scales with a power n of the gas mass, M_G(t). Then f(t) _MV (M_V) = C [M_G(t)]ⁿ, for a summation _MV over all stellar types.

Schmidt gave analytical solutions for n = 0,1,2. He noted that a scale height for HI of 144 pc, a scale height for Cepheids of 80 pc, and a scale height for clusters of 58 pc gave n = 2 to 3. The white dwarf count gave n > 2, the He abundance suggested n = 2, the uniformity of HI suggested n 2, and the cluster mass function gave n = 1 to 2. Schmidt also suggested that with n = 2, dense galaxies like ellipticals should now have less gas than low-density galaxies like the LMC. His final comment was "It is hoped to study the evolution of galaxies in more detail in the future." Following Schmidt (1959), many authors derived scaling relations between the average surface density of star formation, _SFR, and the average surface density of gas. Buat, Deharveng & Donas (1989) included molecular and atomic gas and determined star formation rates from the UV flux corrected for Milky Way and internal extinction. They assumed a constant H₂ / CO ratio and a Scalo (1986) IMF. The result was a good correlation between the average star formation rate in a sample of 28 galaxies and the 1.65 ± 0.16 power of the average total gas surface density. In the same year, Kennicutt (1989) used H for star formation, and HI and CO for the gas with a constant H₂ / CO conversion factor, and determined star formation rates both as a function of galactocentric radius and averaged over whole galaxy disks. For whole galaxies, the average H flux scaled with the average gas surface density to a power between 1 and 2; there was a lot of scatter in this relation and the correlation was better for HI than H₂. More interesting was Kennicutt's (1989) result that the star formation rate had an abrupt cutoff in radius where the Toomre (1964) stability condition indicated the onset of gravitationally stable gas. Kennicutt derived a threshold gas column density for star formation, _crit = / (3.36G) for = 0.7; is the velocity dispersion of the gas; is the epicyclic frequency, and G is the gravitational constant.

In a second study, Kennicutt (1998) examined the disk-average star formation rates using a larger sample of galaxies with H, HI, and CO. He found that for normal galaxies, the slope of the SFR-surface density relation ranged between 1.3 to 2.5, depending on how the slope was measured; there was a lot of scatter. When starburst galaxies with molecular surface densities in excess of 100 M were included, the overall slope became better defined and was around 1.4. This paper also found a good correlation with a star formation rate that scaled directly with the average surface density of gas and inversely with the rotation period of the disk. This second law suggested that large-scale dynamical processes are involved.

Hunter et al. (1998) considered the same type of analysis for dwarf Irregulars and derived a critical surface density that was lower than the Kennicutt (1989) value by a factor of ~ 2. This meant that stars form in more stable gas in dwarf irregulars compared to spirals.

Boissiet et al. (2003) compared _SFR and _gas versus radius in 16 resolved galaxies with three theoretical expressions. The best fits were a SFR dependence on the gas surface density as _{SFR gas}^2.06, a more dynamical law from Boissier & Prantzos (1999) which gave the fit _{SFR gas}^1.48(V / R) for rotation speed V and radius R, and a third type of law from Dopita & Ryder (1994), which fit to _{SFR gas}^0.97 / _tot^0.61. Boissiet et al. (2003) assumed that H₂ / CO varied with radius as the metallicity (Boselli et al. 2002). Their conclusion was that the three laws are equally good, and that for the pure gas law, n > 1.4. Boissiet et al. (2003) also looked for a star formation threshold in the Milky Way. They determined / _crit using both pure-gas for _crit and a gas+star _crit from Wang & Silk (1994). They found that the gas+star _crit gave the best threshold for determining where star formation occurs. The gas alone was sub-threshold throughout the disk.

Zasov & Smirnova (2005) showed that a threshold like _crit may be used to determine the gas fraction in galaxies. If all galaxies have (HI) approximately at the critical _crit = / G, which is proportional to V / R from , then M_gas = _R 2 R _crit dR VR. This was shown to be the case from observations. They also considered that the total mass is M_tot V²R, in which case M_tot / M_gas V, the rotation speed. This was also shown to be confirmed by observations. In their interpretation, small galaxies are more gas-rich than large galaxies because all galaxies have their gas column densities close to the surface density threshold.

For the Milky Way, Misiriotis et al. (2006) used COBE/DIRBE observations to get both the gas and dust distributions and the SFR distribution. They found a gas-law slope of 2.18 ± 0.20, which they claimed was similar to Kennicutt's (1998) bivariate fit slope n = 2.5 for normal galaxies. Luna et al. (2006) determined the Milky Way SFR from IRAS point sources and the CO surface density from a southern hemisphere survey (assuming constant H₂ / CO). They found star formation concentrated in low-shear spiral arms and suggested an additional dependence on shear. Overall they derived _SFR ~ _gas^1.2±0.2. Vorobyov (2003) also suggested a shear dependence for the SFR based on observations of the Cartwheel galaxy, where there is an inner ring of star formation with high shear that is too faint for the normal Kennicutt law, given the gas column density.

1.1. The Q Threshold

A threshold for gravitational instabilities in rotating disks has been derived for various ideal cases. For an infinitely thin disk of isothermal gas, the dispersion relation for radial waves is ² = k^{2 2} - 2 G k + ². Solving for the fastest growth rate gives the wavenumber at peak growth, k = G / ², and the wavelength, = 2² / G , which is on the order of a kiloparsec in main galaxy disks. The dominant unstable mass is M ~ ( / 2)² = ⁴ / G² ~ 10⁷ M in local spirals. The peak rate is given by

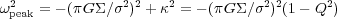(1.1)

which requires Q / G < 1 for instability (i.e., when _peak² < 0).

Disk thickness weakens the gravitational force in the in-plane direction by an amount that depends on wavenumber, approximately as 1 / (1 + kH) for exponential scale height H (e.g., Elmegreen 1987, Kim & Ostriker 2007). Typically, k ~ 1/H, so this weakening can slow the instability by a factor of ~ 2, and it can make the disk slightly more stable by a factor of 2 in Q. On the other hand, cooling during condensation decreases the effective value of the velocity dispersion, which should really be written ^1/2 for adiabatic index that appears in the relation P with pressure P and density . If P is nearly constant for changes in , as often observed, then ~ 0. Myers (1978) found ~ 0.25 for various thermal temperatures at interstellar densities between 0.1 cm^-3 and 100 cm^-3. Thus the effects of disk thickness and a soft equation of state partially compensate for each other.

There is also a Q threshold for the collapse of an expanding shell of gas (Elmegreen, Palous & Ehlerova 2002). Pressures from OB associations form giant shells of gas and cause them to expand. Eventually they go unstable when the accumulated gas is cold and massive enough, provided the induced rotation and shear from Coriolis forces are small. Considering thousands of initial conditions, these authors found that a sensitive indicator of whether collapse occurs before the shell disperses is the value of Q in the local galaxy disk, i.e., independent of the shell itself. The fraction f of shells that collapsed scaled inversely with Q as f ~ 0.5 - 0.4 log₁₀ Q.

The Toomre Q parameter is also likely to play a role in the occurrence of instabilities in turbulence-compressed gas on a galactic scale (Elmegreen 2002). Isothermal compression has to include a mass comparable to the ambient Jeans mass, M_Jeans, in order to trigger instabilities. The turbulent outer scale in the galaxy is comparable to the Jeans length, L_Jeans, which is about the galactic gas scale height, H. If the compression distance exceeds the epicyclic length, then Coriolis forces spin up the compressed gas, leading to resistance from centrifugal forces. So instability needs L_Jeans L_epicycle, which means Q 1, since L_Jeans ~ H ~ ² / G . The epicyclic length is L_epicycle ~ /k, so L_Jeans / L_epicycle = Q.

The dimensionless parameter Q measures the ratio of the centrifugal force from the Coriolis spin-up of a condensing gas perturbation to the self-gravitational force, on the scale where gravity and pressure forces are equal, which is the Jeans length. The derivation of Q assumes that angular momentum is conserved, so the Coriolis force spins up the gas to the maximum possible extent. When Q > 1, a condensing perturbation on the scale of the Jeans length spins up so fast that its centrifugal force pulls it apart against self-gravity. Larger-scale perturbations have the same self-gravitational acceleration (which scales with ) and stronger Coriolis acceleration (which scales with ² / k); smaller-scale perturbations have stronger accelerations from pressure. If angular momentum is not conserved, then the disk can be unstable for a wider range of Q because there is less spin up during condensation. For example, the Coriolis force can be resisted by magnetic tension or viscosity and then the angular momentum in a condensing cloud will get stripped away. This removes the Q threshold completely (Chandrasekhar 1954, Stephenson 1961, Lynden-Bell 1966, Hunter & Horak 1983). In the magnetic case, the result is the Magneto-Jeans instability, which can dominate the gas condensation in low-shear environments like spiral arms and some inner disks (Elmegreen 1987, Elmegreen 1991, Elmegreen 1994, Kim & Ostriker 2001, Kim & Ostriker 2002, Kim et al. 2002). For the viscous case, Gammie (1996) showed that for Q close to but larger than 1, i.e., in the otherwise stable regime, viscosity can make the gas unstable with a growth rate equal to nearly one-third of the full rate for a normally unstable (Q < 1) disk. A dimensionless parameter for viscosity is ³ / G^{2 2}, which is ~ 11 according to Gammie (1996). This is a large value indicating that galaxy gas disks should be destabilized by viscosity. An important dimensionless parameter for magnetic tension is B² / ( G ²) ~ 8, which is also large enough to be important. Thus gas disks should be generally unstable to form small spiral arms and clouds, even with moderately stable Q, although the growth rate can be low if Q is large.

1.2. Modern Versions of the KS Law with ~ 1.5 slope

Kennicutt et al. (2007) studied the local star formation law in M51 with 0.5-2 kpc resolution using Pa- and 24µ + H lines for the SFR, and a constant conversion factor for CO to H₂. There was a correlation, mostly from the radial variation of both SFR and gas surface density, with a slope of 1.56 ± 0.04. There was no correlation with (HI) alone, as this atomic component had about constant column density ( ~ 10 M). The correlation with molecules alone was about the same as the total gas correlation.

Leroy et al. (2005) studied dwarf galaxies and found that they have a molecular KS index of 1.3 ± 0.1, indistinguishable from that of spirals, except with a continuation to lower central H₂ column densities (i.e., down to ~ 10 M pc^-2).

Heyer et al. (2004) found a slope n = 1.36 for _SFR versus (H₂) in M33, where the molecular fraction, f_mol is small. The correlation with the total gas was much steeper. More recently, Verley et al. (2010) studied M33 again and got _{SFR H2}ⁿ for n = 1 to 2, and _{SFR total gas}ⁿ for n = 2 to 4. The steepening for total gas is again because _HI is about constant, so the slope from HI alone is nearly infinite. This correlation is dominated by the radial variations in both quantities, as it is a point-by-point evaluation throughout the disk. Radial changes in metallicity, spiral arm activation, tidal density, and so on, are part of the total correlation. Verley et al. (2010) also try other laws, such as _SFR (_{H2 ISM}^0.5)ⁿ, for which n = 1.16 ± 0.04, and _{SFR ISM}ⁿ, for which n = 1.07 ± 0.02. These differ by considering the conversion from column density to midplane density, using a derivation of the gaseous scale height. The first of these would have a slope of unity if the star formation rate per unit molecular gas mass were proportional to the dynamical rate at the average local (total) gas density. The second has the form of the original Schmidt law, which depends only on density. To remove possible effects of CO to H₂ conversion, Verley et al. also looked for a spatial correlation with the 160 µ opacity, ₁₆₀, which is a measure of the total gas column density independent of molecule formation. They found _{SFR 160}ⁿ for n = 1.13 ± 0.02, although the correlation was not a single power law but a 2-component power law with a shallow part (slope ~ 0.5) at low opacity (₁₆₀ < 10^-4) and a steep part (slope ~ 2) at high opacity.

1.3. Explanations for the 1.5 slope

Prior to around 2008, the popular form of the KS law had a slope of around 1.5 when _SFR was plotted versus total gas column density on a log-log scale. This follows from a dynamical model of star formation in which the SFR per unit area equals the available gas mass per unit area multiplied by the rate at which this gas mass gets converted into stars, taken to be the dynamical rate,

(1.2)

If the gas scale height is constant, then _{gas gas} and _{SFR gas}^1.5. In the model of star formation where star-forming clouds are made by large-scale gravitational instabilities, this 1.5 power law would work only where the Toomre instability condition, Q 1.4, is satisfied. Such a model accounts for the Kennicutt (1989, 1998) law with the Q < 1.4 threshold.

Several computer simulations have shown this dynamical effect. Li et al. (2006) did SPH simulations of galaxy disks with self-gravity forming sink particles at densities larger than 10³ cm^-3. They found a Q threshold for sink particle formation, and had a nice fit to the KS law with a slope of ~ 1.5. Tasker & Bryan (2006) ran ENZO, a 3D adaptive mesh code, with star formation at various efficiencies, various temperature floors in the cooling function, and various threshold densities. Some models had a low efficiency with a low threshold density and other models had a high efficiency with a high threshold density. Some of their models had feedback from young stars. They also got a KS slope of ~ 1.5 for both global and local star formation, regardless of the details in the models. Kravtsov (2003) did cosmological simulations using N-body techniques in an Eulerian adaptive mesh. He assumed a constant efficiency of star formation at high gas density, and star formation only in the densest regions (n > 50 cm^-3, the resolution limit), which are in the tail of the density probability distribution function (pdf; cf. Elmegreen 2002, Krumholz & McKee 2005). Kravtsov (2003) got the KS law with a slope of 1.4 for total gas surface density. Wada & Norman (2007) did a similar thing, using the fraction of the mass at a density greater than a critical value from the pdf (_crit = 10³ cm^-3) to determine the star formation rate. Their analytical result had a slope of 1.5. Harfst, Theis & Hensler (2006) had a code with a hierarchical tree for tracking interacting star particles, SPH for the diffuse gas, and sticky particles for the clouds. They included mass exchange by condensation and evaporation, mass exchange from stars to clouds (via PNe) and from stars to diffuse gas (SNe), and from clouds into stars during star formation. New clouds were formed in expanding shells. Their KS slope was 1.7 ± 0.1. They also got a drop in _SFR at low _gas, not from a Q threshold but from an inability of the gas to cool and form a thin disk (c.f. Burkert et al. 1992, Elmegreen & Parravano 1994).