


The star formation law may also be written as a linear relation for
molecules, with
 SFR
SFR

 H21 (e.g.,
Rownd & Young
1999).
Wong & Blitz
(2002)
found a SFR in direct proportion to
molecular cloud density (n = 1), and suggested that the n
= 1.4 KS law
came from changes in the molecular fraction, fmol =
H21 (e.g.,
Rownd & Young
1999).
Wong & Blitz
(2002)
found a SFR in direct proportion to
molecular cloud density (n = 1), and suggested that the n
= 1.4 KS law
came from changes in the molecular fraction, fmol =
 H2 /
(
H2 /
( HI +
HI +
 H2).
They assumed that H2 / CO was constant and determined the
combined index n' = nmol(1 +
d ln fmol d
ln
H2).
They assumed that H2 / CO was constant and determined the
combined index n' = nmol(1 +
d ln fmol d
ln gas)
where nmol = 1 and fmol increases with
pressure, P. They measured dlnfmol /
d ln P ~ 0.2, and if
P
gas)
where nmol = 1 and fmol increases with
pressure, P. They measured dlnfmol /
d ln P ~ 0.2, and if
P 
 gas2, then d ln
fmol / d
ln
gas2, then d ln
fmol / d
ln gas ~ 0.4.
This gives the KS n = 1.4 law for total gas. Wong &
Blitz also suggested that the stability parameter Q was not a good
threshold for star formation, but a better measure of the gas fraction
in the sense that a high Q corresponds to a low
gas ~ 0.4.
This gives the KS n = 1.4 law for total gas. Wong &
Blitz also suggested that the stability parameter Q was not a good
threshold for star formation, but a better measure of the gas fraction
in the sense that a high Q corresponds to a low
 gas /
gas /
 tot.
Blitz &
Rosolowski (2006)
showed for a wider sample of 13
galaxies that the molecular ratio, Rmol =
tot.
Blitz &
Rosolowski (2006)
showed for a wider sample of 13
galaxies that the molecular ratio, Rmol =
 H2 /
H2 /
 HI,
scales about linearly with the total ISM
pressure. Interacting galaxies had slightly higher
Rmol for a given P, but among interacting
galaxies, the correlation was still present.
HI,
scales about linearly with the total ISM
pressure. Interacting galaxies had slightly higher
Rmol for a given P, but among interacting
galaxies, the correlation was still present.
A large study of HI, CO, and star formation rates from
GALEX ultraviolet and Spitzer 24µ observations was made by
Bigiel et
al. (2008)
and
Leroy et
al. (2008).
They considered the local star
formation law with a resolution of 750 pc. Bigiel et al. found that
 SFR
SFR

 CO, and
that the timescale for
conversion from H2 to stars was about 2 Gyr.
Figure 1 (from
Bigiel et
al. 2008)
shows an example of how much better
the SFR scales with CO than either HI or the total gas. The
CO and SFR maps of NGC 6946 resemble each other closely, and
neither resembles the HI map. Bigiel et al. also found that
CO, and
that the timescale for
conversion from H2 to stars was about 2 Gyr.
Figure 1 (from
Bigiel et
al. 2008)
shows an example of how much better
the SFR scales with CO than either HI or the total gas. The
CO and SFR maps of NGC 6946 resemble each other closely, and
neither resembles the HI map. Bigiel et al. also found that
 HI
saturates to ~ 9
M
HI
saturates to ~ 9
M pc-2. When plotting
pc-2. When plotting
 SFR over
a wide range of
SFR over
a wide range of
 HI+H2,
they found a slope of unity in the molecular range,
HI+H2,
they found a slope of unity in the molecular range,
 HI+H2 > 9
M
HI+H2 > 9
M pc-2, and higher slope in the atomic range
(
pc-2, and higher slope in the atomic range
( HI+H2 < 9
M
HI+H2 < 9
M pc-2). Figure 2 shows the summed
distribution of SFR per unit area versus
total gas column density in 7 spiral galaxies. There is a linear part
at high column density and a steeper part at low column density.
pc-2). Figure 2 shows the summed
distribution of SFR per unit area versus
total gas column density in 7 spiral galaxies. There is a linear part
at high column density and a steeper part at low column density.
 |
Figure 1. Maps of HI, CO and SFR in NGC 6946 with HI on the left, CO in the middle and SFR on the right, all convolved to 750 pc resolution (from Bigiel et al. 2008). The circle is the optical radius at 25 mag arcsec-2. |
Dwarf galaxies look like the outer parts of spirals in the Bigiel et
al. survey, occupying the steeper part of the
 SFR -
SFR -
 gas
diagram at low
gas
diagram at low
 gas.
At higher
gas.
At higher
 HI+H2,
the survey did not have new data, but Bigiel et al. suggested, based on
Kennicutt's (1998)
starburst result, that
perhaps the KS law turned up to a steeper slope (n ~ 1.4) in a third
regime of star formation where
HI+H2,
the survey did not have new data, but Bigiel et al. suggested, based on
Kennicutt's (1998)
starburst result, that
perhaps the KS law turned up to a steeper slope (n ~ 1.4) in a third
regime of star formation where
 H2
exceeds the standard column density of a single molecular cloud (around 100
M
H2
exceeds the standard column density of a single molecular cloud (around 100
M pc-2).
pc-2).
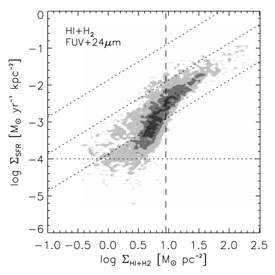 |
Figure 2. The distribution of SFR per unit
area versus total gas column
density, convolved to 750 pc, for 7 spiral galaxies (from
Bigiel et
al. 2008).
There is a change in the slope from ~ 4 at
|
Leroy et al. (2008) compared these new survey results to various theoretical models. They found that the star formation time in CO-rich gas is universally 1.9 Gyr, independent of the average local free fall or orbital time, the midplane gas pressure, the state of gravitational stability of the disk with or without the inclusion of stars in the stability condition, and regardless of the rate of shear or the ability of a cold gas phase to form. Star formation depends only on the presence of molecules and it proceeds at a fixed rate per molecule. Leroy et al. also found that dwarf galaxies are forming stars at their average historical rate, whereas spirals are forming stars at about half of their average rate. In the outer disk, the SFR in HI drops with radius faster than the free fall time, suggesting self-gravity is not the lone driver. Also important are the phase balance between HI and H2, giant molecular cloud (GMC) destruction, stellar feedback, and other processes. These processes govern the presence of GMCs with an apparently constant star formation efficiency in each GMC.
Unlike the star formation rate per molecule, the molecule-to-atom ratio does correlate well with environmental parameters. Leroy et al. (2008) showed approximately linear correlations with stellar surface density and interstellar pressure, an inverse squared dependence on the orbit time, and an exponential dependence on the galactic radius, like the rest of the disk, and with a comparable radial scale length. The molecular fraction is a smooth function of environmental parameters (e.g., pressure); no thresholds were seen. Disks seem to be marginally stable throughout.
Leroy et al. concluded by noting that the HI-H2
transition in spirals typically occurs at 0.43 ± 0.18
R25, which is about the same as where
 stars =
81 ± 25
M
stars =
81 ± 25
M pc-2,
pc-2,
 gas = 14
± 6 M
gas = 14
± 6 M pc-2, P = 2.3 ± 1.5 × 104
kB K cm-3,
and Torbit = 1.8 ± 0.4 Gyr. There should be
unobserved H2 in dwarfs, according to the high star
formation rates and
low CO emissions there; in fact Leroy et al. estimate for dwarfs
pc-2, P = 2.3 ± 1.5 × 104
kB K cm-3,
and Torbit = 1.8 ± 0.4 Gyr. There should be
unobserved H2 in dwarfs, according to the high star
formation rates and
low CO emissions there; in fact Leroy et al. estimate for dwarfs
 H2 ~
2
H2 ~
2 HI in
the inner regions.
HI in
the inner regions.
Where  HI >
HI >
 H2, the
star formation efficiency is proportional to
H2, the
star formation efficiency is proportional to
 stars, making
stars, making
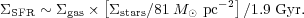 |
(2.1) |
2.1. Theoretical Models for the Bigiel-Leroy Observations
Krumholz et
al. (2008)
considered the molecule formation problem by starting with
the radiative transfer of H2-dissociating radiation:
dF / dz = -n
 d F -
fHI n2 R /
fdiss. Here,
F is the flux in Lyman-Werner bands that dissociate
H2, n
is the density ( ~ 30 cm-3 near the H2 transition),
d F -
fHI n2 R /
fdiss. Here,
F is the flux in Lyman-Werner bands that dissociate
H2, n
is the density ( ~ 30 cm-3 near the H2 transition),
 d is the dust
cross section per H (10-21 cm2),
fHI is the fraction of n that is HI, R
is the rate coefficient for formation of H2 on grains
( ~ 3 × 10-17 cm3 s-1; i.e., the
formation rate is
fHI n2 R), and
fdiss is the fraction of uv
photon absorptions that dissociate H2 ( ~ 0.1).
d is the dust
cross section per H (10-21 cm2),
fHI is the fraction of n that is HI, R
is the rate coefficient for formation of H2 on grains
( ~ 3 × 10-17 cm3 s-1; i.e., the
formation rate is
fHI n2 R), and
fdiss is the fraction of uv
photon absorptions that dissociate H2 ( ~ 0.1).
The solution to this radiative transfer equation is
F( ) =
(e-[
) =
(e-[ -
-
 HI] - 1)
/
HI] - 1)
/  where
where
 HI = ln(1 +
HI = ln(1 +
 );
);
 = fdiss
= fdiss
 d
c E0 / nR is the ratio of absorption in
dust to H2, and
E0 is the free space photon number density
(~ 7.5 × 10-4 cm-3).
Krumholz et
al. (2008)
assume that the cold neutral density comes from two phase
equilibrium. Then n scales with E0 and
d
c E0 / nR is the ratio of absorption in
dust to H2, and
E0 is the free space photon number density
(~ 7.5 × 10-4 cm-3).
Krumholz et
al. (2008)
assume that the cold neutral density comes from two phase
equilibrium. Then n scales with E0 and
 becomes nearly constant. From
this they get the extinction, AV, to the HI/H2
transition, the HI column density,
becomes nearly constant. From
this they get the extinction, AV, to the HI/H2
transition, the HI column density,
 HI, and
the molecular fraction in spherical cloud complexes as a function of
the complex total column density. They do this also as a function of
metallicity.
HI, and
the molecular fraction in spherical cloud complexes as a function of
the complex total column density. They do this also as a function of
metallicity.
After considering a galactic cloud population,
Krumholz et
al. (2009a)
derive  HI
versus
HI
versus
 total gas
for different
metallicities, and compare this with observations of galaxies having
those metallicities. They do the same for H2. They also
compare the observed versus the predicted correlation between
H2 / HI and pressure P. To do this, they use the observed
total gas
for different
metallicities, and compare this with observations of galaxies having
those metallicities. They do the same for H2. They also
compare the observed versus the predicted correlation between
H2 / HI and pressure P. To do this, they use the observed
 total gas
and metallicity, and then compute RH2 =
total gas
and metallicity, and then compute RH2 =
 H2 /
H2 /
 HI from
theory. This is plotted versus the observed pressure from
Blitz &
Rosolowski (2006)
and
Leroy et
al. (2008).
The agreement is good.
HI from
theory. This is plotted versus the observed pressure from
Blitz &
Rosolowski (2006)
and
Leroy et
al. (2008).
The agreement is good.
Krumholz et al. (2009b) considered the star formation law,
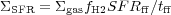 |
(2.2) |
where the star formation rate in a free fall time is the fraction of
the gas that turns into stars in a free fall time, SFRff,
divided by the free fall time, tff. This is
SFRff /
 ff =
(M6-0.33 / 0.8 Gyr) × Max[1,
ff =
(M6-0.33 / 0.8 Gyr) × Max[1,
 gas / 85
M
gas / 85
M pc-2]; M6 is the
cloud mass in units of 106
M
pc-2]; M6 is the
cloud mass in units of 106
M . This
equation assumes that
stars form in the high density tail of a log-normal density pdf, with
the tail width given by the Mach number; a fraction of 0.3 of the dense
gas mass goes into stars. The clouds are virialized and at uniform
pressure until the galactic
. This
equation assumes that
stars form in the high density tail of a log-normal density pdf, with
the tail width given by the Mach number; a fraction of 0.3 of the dense
gas mass goes into stars. The clouds are virialized and at uniform
pressure until the galactic
 gas
exceeds the column density of a single GMC; then the pressure equals the
galactic pressure. Also, the cloud complex mass is taken to be
M6 =
37
gas
exceeds the column density of a single GMC; then the pressure equals the
galactic pressure. Also, the cloud complex mass is taken to be
M6 =
37 gas / (85
M
gas / (85
M pc-2) from the galaxy Jeans mass.
pc-2) from the galaxy Jeans mass.
This theory for molecule formation and star formation in a galactic environment fits well to the observations by Bigiel et al. (2008) and Leroy et al. (2008). It reproduces the low column density regime by having a low ratio of molecules to atoms at low pressure, it reproduces the intermediate column density regime by having a fixed star formation rate per molecule and an areal average star formation rate from the areal density of molecular clouds at constant pressure, and it reproduces the high column density regime by increasing the interstellar pressure, which makes the cloud density go up and the free fall time go down. A key point in their model is that molecular cloud pressures are constant in normal galaxy disks because they are set by HII region pressures (feedback) and not the galactic environment. In this sense, all GMCs have to be parts of shells or other active disturbances formed by high pressures.
We know that molecular cloud pressures in the Milky Way are about constant from the Larson (1981) laws, which require this for virialized clouds, but we don't really know the reason for it. It could be feedback, as Krumholz et al. (2009b) suggest, or it could be the weight of the HI shielding layer, which has a regulatory effect on pressure (Elmegreen 1989). This regulatory effect works because at high ambient pressure, the atomic density on the periphery of molecular clouds is high and so the required surface column density for H2 line self-shielding is low, and vice versa. The pressure at the bottom of the shielding layer, which is the molecular cloud surface pressure, scales directly with the column density of the shielding layer. Thus a lower intercloud pressure is compensated by a higher HI column density at the molecular cloud surface, making the molecular cloud surface pressure somewhat uniform.
Robertson & Kravtsov (2008) simulated star formation in galaxies. They took a star formation rate per unit volume
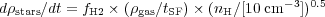 |
(2.3) |
where
tSF = tff /
 ff is the
free fall time, tff, divided by the fraction of the
gas that turns into stars in a free fall time,
ff is the
free fall time, tff, divided by the fraction of the
gas that turns into stars in a free fall time,
 ff =
0.02. To determine the
molecular fraction, fH2, they considered heating and
cooling, a radiation field proportional to the SFR, the
Sternberg, et
al. (2002)
H2 formation theory, and radiative transfer using the
Cloudy code. The result was a SFR that scaled steeply with the
total gas column density, as observed, a higher KS slope for lower mass
galaxies, which is also observed, and a shallower KS slope for the
H2 column density alone, as in the molecular KS law. These
results were somewhat independent of galaxy mass. The molecular/atomic
ratio also scaled with pressure in an approximately linear fashion,
regardless of galaxy mass, as observed. They also found a stability
parameter Q that ranged from unstable in the inner, star-forming
parts of the disk, to stable in the outer regions.
ff =
0.02. To determine the
molecular fraction, fH2, they considered heating and
cooling, a radiation field proportional to the SFR, the
Sternberg, et
al. (2002)
H2 formation theory, and radiative transfer using the
Cloudy code. The result was a SFR that scaled steeply with the
total gas column density, as observed, a higher KS slope for lower mass
galaxies, which is also observed, and a shallower KS slope for the
H2 column density alone, as in the molecular KS law. These
results were somewhat independent of galaxy mass. The molecular/atomic
ratio also scaled with pressure in an approximately linear fashion,
regardless of galaxy mass, as observed. They also found a stability
parameter Q that ranged from unstable in the inner, star-forming
parts of the disk, to stable in the outer regions.
2.2. Observations and Models of Outer Disks
Murante et
al. (2010)
have a multi-phase SPH code that assumes pressure
determines the molecular abundance, and the molecules give the SFR.
Below
 total gas
~ 10 M
total gas
~ 10 M pc-2, the slope of
the molecular star formation law turns out to be very steep,
pc-2, the slope of
the molecular star formation law turns out to be very steep,
 SFR
SFR

 total
gasn for n ~ 4. Above 10
M
total
gasn for n ~ 4. Above 10
M pc-2, the slope is the same as in the
Kennicutt law, n = 1.4, which is steeper than in
Bigiel et
al. (2008),
where n ~ 1 for the molecular Schmidt law.
pc-2, the slope is the same as in the
Kennicutt law, n = 1.4, which is steeper than in
Bigiel et
al. (2008),
where n ~ 1 for the molecular Schmidt law.
Bush et al. (2010)
simulated galactic star formation with special attention
to the outer disks. The star formation model followed
Springel &
Hernquist (2002)
with radiative cooling, star formation in the cold phase, no specific
molecular phase, and a volume-Schmidt law,
 SFR
SFR

 total
gas1.5. They found patchy star
formation in the outer parts, usually along spiral arcs where the gas
density was high. This morphology is in agreement with GALEX
observations
(Thilker et
al. 2005,
Gil de Paz et
al. 2005).
The Bigiel et al. and Leroy et
al. observations were matched qualitatively in these outer parts too:
below
total
gas1.5. They found patchy star
formation in the outer parts, usually along spiral arcs where the gas
density was high. This morphology is in agreement with GALEX
observations
(Thilker et
al. 2005,
Gil de Paz et
al. 2005).
The Bigiel et al. and Leroy et
al. observations were matched qualitatively in these outer parts too:
below  gas
~ 10 M
gas
~ 10 M pc-2, the slope n ~ 6
to 8 was steeper than in the observations (which also plot SFR versus
total gas in the outer regions). Then it was less steep at higher
column density, with a slope of n ~ 1.4, which agrees with the
Kennicutt (1998)
slope for total gas.
pc-2, the slope n ~ 6
to 8 was steeper than in the observations (which also plot SFR versus
total gas in the outer regions). Then it was less steep at higher
column density, with a slope of n ~ 1.4, which agrees with the
Kennicutt (1998)
slope for total gas.
Outer disks can be Toomre-stable on average because the gas and star
column densities are very low. This is especially true for dwarf
galaxies
(Hunter et
al. 1998).
It might be that magnetic fields and
viscosity destabilize outer disks, as discussed in
Section 1.1, but in any case, outer
disks appear to be much more
stable than inner disks. More importantly, the gas is outer disks is
often far from uniform and the use of an average column density for Q
is questionable. Locally there can be islands of high column density
where Q is small enough to be in the unstable region
(van Zee et
al. 1996).
These islands have to be larger than the Jeans mass, which might be
107 M . Spiral arms and large disturbances in pressure could
make unstable regions like this.
Dong et al. (2008)
found unstable islands
of star formation in the outer part of M83. In these regions, the star
formation followed a steep KS law from point to point with a slope of
about 1.4
(Dong et
al. 2008).
. Spiral arms and large disturbances in pressure could
make unstable regions like this.
Dong et al. (2008)
found unstable islands
of star formation in the outer part of M83. In these regions, the star
formation followed a steep KS law from point to point with a slope of
about 1.4
(Dong et
al. 2008).
Bigiel et al. (2010a) found that outer disk star formation seen by GALEX follows the HI very well in M83, with a uniform consumption time of 100 Gyr per atom beyond 1.5R25. The form of the star formation is mostly in spiral arms. Outer disk arms could be spiral waves radiating from the inner disk (Bertin & Amorisco 2010).
Boissier et al. (2008) observed the galaxy-integrated KS law in low surface brightness galaxies, using a SFR from GALEX NUV observations. For a given total HI mass, the star formation rate was low by a factor of ~ 5 compared to normal spirals, but over the whole range, the total star formation rate scaled directly with the HI mass. This is not the same as saying that the star formation rate per unit area scales directly with the HI column density because the observations are spread out in a plot like this with big galaxies on one side and small galaxies on the other.
Bigiel et al. (2010b) studied SF rates in the far-outer disks of 17 spiral and 5 dwarf galaxies, where the gas is highly HI dominated. The SF laws compare well with those in dwarf galaxies. There is no obvious Q threshold. They suggest that the total SF Law has three components, the extreme outer disk component that is HI dominated, a transition region where the molecular fraction increases to near unity, the molecular region inside of that, and the starburst component, where the surface density is higher than that of a single GMC.
2.3. Scaling relations inside individual clouds
Krumholz & Tan (2007) showed that the conversion rate from gas to stars per unit free fall time is about constant inside clouds over a wide range of densities. This implies that the SFR per unit volume scales with the 1.5 power of density, with the first 1 in the power coming from the mass per unit volume, and the 0.5 in the power coming from the free fall rate. This is like a KS law, but for individual GMCs. There is also a threshold column density for star formation inside GMCs of around ~ 5-7 mag in V (Johnstone et al. 2004, Kirk et al. 2006, Enoch et al. 2006, Jørgensen et al. 2007).
Chen et al. (2010)
studied the KS relation for individual GMCs in the LMC.
They measured the star formation rate from both HII regions and
by direct counting of young stellar objects. For YSO counting, the rate
per unit area inside a cloud approximately satisfies the total-gas
Kennicutt relation with the same time scale per atom, ~ 1 Gyr. For
these regions,  HI+H2 ~ 100
M
HI+H2 ~ 100
M pc-2, larger than in the main parts of galaxy disks. Chen et al.
also found that the areal rate of star formation was much lower in the
long molecular ridge south of 30 Doradus than in the GMCs. Presumably
this ridge is not strongly self gravitating, even though it is CO-rich.
pc-2, larger than in the main parts of galaxy disks. Chen et al.
also found that the areal rate of star formation was much lower in the
long molecular ridge south of 30 Doradus than in the GMCs. Presumably
this ridge is not strongly self gravitating, even though it is CO-rich.