Annu. Rev. Astron. Astrophys. 2004. 42: 275-316 Copyright © 2004 by Annual Reviews. All rights reserved

2. TURBULENCE AND CHEMICAL INHOMOGENEITY

The degree to which turbulence and other transport processes mix or homogenize the gas in the face of repeated local pollutions by supernovae and other sources of fresh metals could provide an important constraint on the hydrodynamics of the ISM. This general problem is called passive scalar turbulence because the particles being transported have no effect on the velocity field. A review of experiments involving incompressible turbulent scalar transport can be found in Warhaft (2000), who emphasized that passive scalar probability density functions (pdfs) usually have strong exponential tails. A review focussing on a particular class of theoretical approaches has been given by Falkovich, Gawedzki & Vergassola (2001), whereas reviews of methods to calculate the concentration pdf and its moments are in Dopazo (1994) and O'Brien (1980). Briefer and more specialized treatments can be found in Shraiman & Siggia (2000) and Pope (2000, section 12.4).

Here we summarize observations of abundance variations in stars and gas, and we review recent theoretical work on interstellar turbulent mixing. We do not discuss star-to-star variations in globular clusters that may be affected by stellar evolution (Yong et al. 2003).

2.1. Metallicity Fluctuations: Observations

Recent observations of metallicity dispersions in stars of the same age and in interstellar gas suggest that the ISM is very well mixed on average, with typical fluctuations about the mean of only 5-20%. This low value is a challenge to explain considering the spotty pollution of new elements from supernovae and other sources. In addition, there are much larger observed fluctuations in a few places, suggesting the overall distribution function for abundance has a long, non-Gaussian tail. Both the low dispersion and the long tail might be explained by interstellar turbulence.

Stars of a similar age have often shown large variations in metallicity (a term usually referring to iron abundance relative to the Sun). For example, Edvardsson et al. (1993) and Chen et al. (2000) found factor-of-four abundance variations in several elements for F and G main sequence stars. After correcting for selection effects, Edvardsson et al. estimated that the dispersion at a given age is about 0.15 to 0.20 dex, i.e., 40-60%, whereas Garnett & Kobulnicky (2000) suggested it is smaller than 0.15 dex for the same sample. A large unbiased sample of over 550 Hipparcos stars with homogeneous chromospheric age estimates and photometric metallicities showed a dispersion at a given age of only 0.13 dex (Rocha-Pinto et al. 2000). Reddy et al. (2003) studied 27 elements in 181 F and G stars and found a dispersion at a given age that is somewhat smaller than in Edvardsson et al. (1993) and Chen et al. (2000). Feltzing & Gonzales (2001) used an inhomogeneous sample of 5828 stars and found a larger scatter in the metallicity at a given age of 0.2 to 0.3 dex, which exceeds the observational errors. A major problem is that the ages of the stars used in these studies have large uncertainties. Considering that the stellar orbits probably migrated and led to additional abundance variations from Galactic radial gradients (e.g., Wielen et al. 1996), the stellar results are consistent with a dispersion in the gas of 20-30% or less, the upper limit set by uncertainties inherent in field star samples.

Other evidence for homogeneity among field stars comes from elemental abundance ratios. Reddy et al. (2003) estimated the intrinsic scatter in the ratio [X/Fe] for element X by fitting a Gaussian curve to the histogram of deviations between [X/Fe] and the linear fit of [X/Fe] versus [Fe/H]. The standard deviations in the Gaussian for 26 elements in 181 stars varied between 0.03 and 0.10 dex. These deviations are comparable to the errors, so the result is an upper limit to the intrinsic scatter. It does not depend on stellar age, as do the absolute abundances. Reddy et al. noted that because the elements come in differing proportions from different sites of stellar nucleosynthesis, the lack of scatter implies all the ejecta were well-mixed in the gas before the stars formed.

Abundance fluctuations of 0.05-0.15 dex had also been found in studies of open clusters (e.g., Friel & Boesgaard 1992, Twarog et al. 1997, Carraro et al. 1998), B stars in star-forming regions (e.g., Cunha & Lambert 1994) and clusters (Rolleston et al. 1994), the Magellanic clouds (e.g., Olszewski et al. 1991), the interstellar medium (Meyer et al. 1998), Galactic H II regions (Deharveng et al. 2000), and H II regions in disk (see review in Henry & Worthey 1999) and dwarf irregular (e.g., Thuan et al. 1995) galaxies.

However, F stars in nearby open clusters (Friel & Boesgaard 1992 and references therein) show no evidence for star-to-star abundance variations at the level of detectability. Cluster-to-cluster variations are also small, including clusters of all ages, and essentially zero (less than 10-20%) for the four clusters younger than 4 × 10⁸ years. The latter result implies that the ISM is mixed, at least to this level, for scales between ~ 1 pc (the size of the clumps from which clusters form) and ~ 100 pc (the distances between clusters) on a timescale less than 4 × 10⁸ years. Even more stringent constraints were found from the photometric metallicity study of 76 clusters by Twarog et al. (1997). Comparison of high-precision photometry with stellar evolution models suggested a metallicity spread less than ~ 0.03 dex in the Hyades cluster (Quillen 2002). Paulson, Sneden & Cochran (2003) derived the same small [Fe/H] spread, excluding three outlier stars, using spectroscopic abundance determinations for individual stars. These results imply fluctuations of less than ~ 7% in the gas from which the Hyades cluster formed.

Interstellar absorption studies suggest equally low dispersions. Meyer et al. (1998), Moos et al.(2002), and Andre et al. (2003) found oxygen abundance dispersions over distances of around one kpc that are only a few percent. A recent study of interstellar Kr/H by Cartledge, Meyer & Lauroesch (2003) found a spread about the mean of only 0.06 dex for lines of sight within the local Orion spur; this was less than the measurement error.

We conclude that the most recent evidence, based on field stars of a given age, cluster stars, and the ISM, suggests a metallicity dispersion that is very small, less than 20 to 30% and perhaps as small as a few percent. This small Galactic dispersion is consistent with the study of 41 H II regions in M101 by Kennicutt & Garnett (1996).

There are notable exceptions, though, including: (a) the existence of old super-metal-rich stars (e.g., Feltzing & Gonzalez 2001), and a large range in abundance ratios among metal-poor stars (Fields et al. 2002); (b) the lack of an age-metallicity relation for five nearby clusters, which led Boesgaard (1989) to conclude that local abundance fluctuations of ~ 0.2-0.3 dex must persist for at least 10⁸-10⁹ years (but see Friel & Boesgaard 1992 for a revised result); (c) the factor of 2 to 3 fluctuations in [O/H] among subgroups in Orion (Cunha & Lambert 1994), which, however, may be a result of self-pollution; (d) the study of B stars in several clusters at galactocentric distance ~ 13 kpc that indicates one cluster has [Fe/H] larger than the rest by a factor of ~ 5 (Rolleston, Dufton & Fitzsimmons 1994), (e) two stars in the Carina nebula (Andre et al. 2003) that are separated by only a few hundred parsecs but have line-of-sight oxygen abundances different by about 40%, and (f) outlier stars in the cluster studies discussed earlier.

These examples suggest a metallicity pdf with a small variance and possibly large higher moments, i.e., a fat tail at large metallicities. Such a pdf is similar to that found for the pdf of passive scalars in incompressible turbulence (Warhaft 2000). The analogous pdf for a compressible, magnetic, and self-gravitating ISM is unknown.

2.2. How Large Should Metallicity Fluctuations Be?

Theoretical investigations of abundance fluctuations have until recently nearly all been based on order of magnitude arguments involving characteristic spatial scales and timescales for various processes. Two of the more thorough discussions are in Roy & Kunth (1995) and Tenorio-Tagle (1996). Regarding spatial scales, Elmegreen (1998) pointed out that for a hierarchically structured ISM with star formation operating on a local dynamical time, the size of an O and B star association is usually larger than the supernovae remnants it produces. Unless there is some immediate mixing, as in hot ionized or evaporating flows, the new elements should be spotty and variable for subsequent generations of stars (self-enrichment). The point about timescales was highlighted by Reeves (1972): The mean time for a gas element to get reincorporated into a star is shorter than the time for its dispersal by supernova mixing, so abundance fluctuations should be large. Both results contradict the apparent uniformity of abundances inside and between clusters and in the general ISM.

Estimates for mixing times have changed since Reeves' (1972) paper. Edmunds (1975) found that the timescale for mixing of gas by turbulence and galactic shear is relatively short compared with the star formation time, provided the sources of metals do not cluster together making the dispersion more difficult (Kaufman 1975). Bateman & Larson (1993) also derived a short mixing time, considering diffusion by cloud motions, as did Roy & Kunth (1995), who applied the diffusion approximation to galactic shear, radial flows, turbulent diffusion, supernovae, and gas instabilities. Similarly short timescales can be derived using structure functions by considering the separation of initially nearby Lagrangian fluid particles (Frisch 1995). This latter procedure is often used to derive the Richardson 4/3 law of superdiffusive incompressible turbulence. The implication of these short mixing times is that the ISM should be homogeneous.

The expectation of large spatial fluctuations may be viewed in a different way too, by considering the number of overlapping regions of contamination. Edmunds (1975) showed that n supernovae in a local volume should lead to inhomogeneities of order n^-1/2 if there is no subsequent mixing. Adopting an average of n ~ 5 × 10⁴, he suggested that fluctuations would be relatively small. More detailed models for overlapping contaminations were studied by Roy & Kunth (1995), Argast et al. (2000) and Oey (2000). Oey (2003) used turbulent dispersal from Bateman & Larson (1993) to enlarge the effective sizes and reduce the average metallicities in the overlapping regions. Low metallicity stars and galaxies should have large metallicity dispersions because the numbers of contaminating events are small (Audouze & Silk 1995).

A problem with most of the timescale arguments is that they apply to turbulent transport and not homogenization. Moving clouds around or shredding them with fluid instabilities does not homogenize the gas at the atomic level or change the frequency distribution of abundance concentrations; viscosity and molecular diffusion are required for that. The same is true for incompressible turbulence imagined as a cascade of vortices. Unless the advection process creates steep gradients on small scales, molecular diffusion cannot occur in a reasonable time. The situation changes when there are large-scale gradients in the mean concentration; then advection from distant regions can change the concentration distribution locally (see Equation 2 below). Even so, homogenization requires molecular diffusion. Thus, a small transport time in the ISM does not imply the gas will homogenize enough to remove abundance differences before it forms stars and clusters. The size and placement of each protostellar core within the complex spatial pattern of abundance fluctuations will determine its metallicity.

Releasing metals into the interstellar turbulent gas is similar in basic respects to dropping a blob of ink into a turbulent fluid. Figure 1 shows such a release into a two-dimensional (2D) incompressible forced chaotic velocity field (Jullien et al. 2000). Advection spreads the scalar out in space, while concentrating it locally through stretching and folding, shearing it into thin ribbons until the spatial gradients are large enough that molecular diffusion becomes significant in the third frame. By the final frame, diffusion has smeared out most of the striated structures.

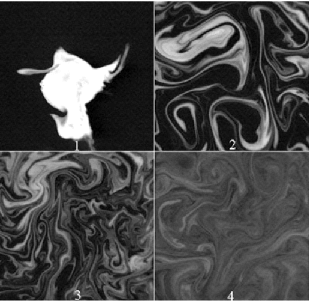Figure 1. This sequence of four time steps shows a blob of dye released into an incompressible two-dimensional laboratory turbulent fluid that is forced by a chaotic velocity field with a single large scale. The evolution of this concentration field illustrates some of the basic features that can be expected for passive scalars like newly produced elements or dust grains released into the ISM: Nonlinear advection transports concentration away from the source but concentrates it locally through stretching and folding into thin regions of large velocity gradients where molecular diffusion eventually results in true mixing. From Jullien et al. (2000).

How does turbulence deliver gradients to small enough scales for molecular diffusion to cause homogenization in a reasonable time? de Avillez & Mac Low (2002) found a surprisingly long timescale for the decay of the variance in a passive scalar field that had an initial checkerboard pattern and was mixed by supernovae. Their time scaled to a galaxy (at least a few times 10⁸ years) is larger than previous estimates and still is a lower limit because they did not include sources of new metals. de Avillez & Mac Low also found that the mixing time is independent of the mixing length, unlike mixing modeled as diffusion, and that the mixing time decreases with increasing supernova rate as a result of the increased velocities.

There may be ways other than turbulence to get gradients on small enough scales for molecular diffusion to homogenize. In Tenorio-Tagle's (1996) "fountain with a spray" model, metal-rich droplets falling onto the disk are subject to Rayleigh-Taylor instabilities that reduce their size even further; diffusion will be very effective in such a situation.

2.3. Methods of Analysis

There are many methods for studying passive scalar turbulent transport. Here we describe two approaches: prescribed artificial velocity fields and closure methods for studying restricted properties of turbulent transport.

2.3.1. Artificial stochastic velocity fields

Most of what is known about passive scalar turbulence comes from models using an idealized velocity field that is not a rigorous solution to the hydrodynamics equations (see review by Falkovich et al. 2001). An example would be a time-uncorrelated velocity field with Gaussian statistics, a prescribed spatial correlation function, and a constraint of incompressibility. This is called a Kraichnan velocity field (e.g., Shraiman & Siggia 2000). The advantages of such a field are that the equations for the concentration field and its statistical properties can in some cases be solved analytically without a closure assumption, and the generic properties of the result might be valid for any velocity field that has the same variance and conservation constraints. However, there is a large danger in assuming a delta function for the time correlation function.

Large intermittency in the velocity gradient field means that a large fraction of the fluid contains large gradients compared with a Gaussian. In incompressible turbulence (and the ISM - see Interstellar Turbulence I), this fraction gets larger on smaller scales. This implies that intermittency should homogenize the gas faster than purely Gaussian motions, because molecular diffusion depends on large velocity gradients at small scales.

Decamp & Le Bourlot (2002) used another model velocity field that was obtained from a wavelet reconstruction with statistical properties similar to the ISM velocity field, including motions correlated in space and time. They solved the continuity equations and showed that the correlated velocity field has a faster dispersion and a larger standard deviation for passive scalars (by factors of 2 to 4) than an uncorrelated Gaussian velocity field. The spatial distributions for species undergoing chemical reactions were also different, suggesting a mechanism for molecular segregation in dense clouds (Section 3). Further work on turbulent mixing using synthetic velocity fields is in Elliott & Majda (1996), Fung & Vassilicos (1998), and Boffetta et al. (1999).

2.3.2. Closure methods: PDF and moment equations

For some purposes, it may be sufficient to understand how the mean, variance, and skewness of a metallicity distribution depend on the source terms and large-scale gradients. This is the moment approach, and it has the advantage that some of its results can be obtained analytically. The moment approach might explain, for example, why there is an inverse square root scaling on the supernova rate for the decay timescale of the abundance variance (de Avillez & Mac Low 2002). The evolution equation for the one-point probability distribution of metallicities was derived rigorously for incompressible turbulence by Dopazo, Valino & Fueyo (1997), who also derived the moment equations for incompressible flow (see also O'Brien 1980; Chen & Kollman 1994; Dopazo 1994; Pope 1994, 2000).

Perhaps the simplest question that can be asked about scalar turbulence concerns the way in which the average relative concentration <Z> of a local patch of contaminant (relative to hydrogen, for example) will spread in space as a function of time. The usual place to start is to examine the mean square distance, <x²(t)>, traveled by a marked Lagrangian fluid particle. This distance can be related to an integral over the Lagrangian correlation function, assuming only statistically stationary and isotropic turbulence. Without knowing the correlation function, however, this relation is of little use. An approximation is to use the fact that the correlation is unity at time zero and approaches zero for large separations. Then for times much smaller than the correlation time T_L = ₀ R() d, x_rms = v_rms t whereas at t >> T_L, x_rms = 2^1/2 v_rms(T_L t)^1/2. Here, R() is the two-time correlation function at a given point in the flow for lag ; i.e., R() = <u(t) u(t + )> / ² for flow speed u and the average <> is over all pairs of points separated by . Normalization to the variance, ² = <u(t) u(t)>, makes R() dimensionless with values between -1 and 1. In this formulation, the particle behaves ballistically at short times and has an uncorrelated random walk at large times. These results are usually referred to as Taylor's theorem (Taylor 1921; see McComb 1990; Pope 2000). The result is important for illustrating the nature of turbulence as a correlated random walk and the analogy between turbulent and molecular diffusion, where in the latter case T_L would be the mean collision time.

Klessen & Lin (2003) recently showed that Taylor's theorem is correct in 3D-compressible turbulence. McComb (1990), Piterbarg & Ostrovskii (1997) and others have pointed out that Taylor's theorem does not solve the problem of turbulent dispersal and transport, even for the mean field because what is required is information in the lab frame, not following the particle. Klessen & Lin (2003) suggest that the result can be used to develop a phenomenological mixing-length or diffusion model for turbulent transport in the ISM in which the integral correlation time is related to the mean time between shock passages.

Another fundamental relationship is Richardson's law (Richardson 1926) for the rate at which pairs of points separate in space in the inertial range of turbulence. One form of this law states that the time dependence of the rms separation is t^3/2 (Falkovich et al. 2001, Boffetta & Sokolov 2002, Nicolleau & Vassilicos 2003). Work on pair dispersion using synthetic velocity fields has resulted in at least two important insights: (a) The dynamics of particle pairs is sensitive to initial conditions but their rms separation increases algebraically, not exponentially (unlike low-dimensional chaotic systems). (b) Particle pairs travel together for long times and then separate explosively when they encounter straining regions around hyperbolic points in the flow (e.g., Nicolleau & Vassilicos 2003).

A traditional approach that could be applied to the spreading of newly produced elements from sources in the ISM is to ignore the detailed dynamics and use an equation for the evolution of the mean concentration field alone. In general, the concentration Z of an element evolves in a given velocity field u as

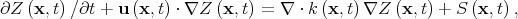(1)

where k is the mass diffusivity and S is the rate at which sources inject the element. The second term on the left represents the effect of the turbulent velocity field in advecting the concentration field. For the interstellar medium this velocity field will consist of complex compressions and vortical motions. The first term on the right represents molecular diffusion, which operates only on small scales in regions where the gradient of the concentration field is large. This equation illustrates how turbulent advection of a passive scalar spreads it out in space while increasing the local gradients through stretching, compressing, and folding. Molecular diffusion then operates where the gradients are high.

Timescales for molecular diffusion have been discussed recently by Oey (2003) for a uniform gas. The result is sensitive to temperature, so most of the homogenization of elements in the ISM may occur in the hot regions, like superbubbles (Silich et al. 2001), as well as those with the steepest velocity gradients.

To obtain the time evolution of the average concentration, one might choose to ignore all the details of the turbulence and spatially average Equation 1. Ignoring also the molecular diffusion and source terms, we get

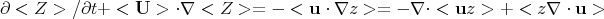(2)

for mean concentration and velocity < Z > and < u > and fluctuating parts z and u. The last term is zero for incompressible turbulence, leaving only - ⋅ <u z>, which contains the unknown ensemble average of the scalar flux, <uz>, representing interactions between the fluctuating parts of the velocity and concentration fields. This is a classic closure problem. We could derive a differential equation for the scalar flux, but it would contain more unknown correlations, including triple correlations, and further manipulation only leads to higher and higher order unknowns.

In the incompressible case, the simplest treatment is to imagine that the turbulent transport behaves diffusively, like molecules in a gas. Then the scalar flux is proportional to the mean concentration gradient and given by

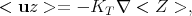(3)

where K_T is a scalar diffusivity given by some timescale times the square of some velocity. Often these are taken to be the correlation time and the rms velocity, although a variety of other forms have been used to fit specific experimental results (Piterbarg & Ostrovskii 1997). Using Equation 3, Equation 2 becomes the usual diffusion equation, and the patch of concentration, if initially a point source, would spread according to a Gaussian whose width grows r ~ t^1/2.

In fact, turbulent transport cannot be described by classical diffusion because triple correlations are as important as quadratic correlations, or, more physically, turbulent motions are not random independent steps but correlated bulk transports over a wide range of scales.

There have been many attempts, all unsuccessful to various degrees, to develop closure techniques for passive scalar turbulence. Many of these are described in reviews by O'Brien (1980) and Dopazo (1994). Perhaps the most popular in the physics community is the mapping closure suggested by Chen, Chen & Kraichnan (1989). A more complicated closure method is based on the Eddy-Damped Quasinormal Markovian approximation (Lesieur 1990). An application of this closure to the passive scalar problem with reference to earlier work is in Herr, Wang & Collins (1996).

A promising approach that is not too complex yet captures the importance of the triple correlations was proposed by Blackman & Field (2002) in connection with turbulent dynamo theory and then applied to the scalar turbulence problem (Blackman & Field 2003). The idea is to model the time derivative of the scalar flux as a normal diffusion term with an eddy viscosity plus a damping term <uz> / , where is a relaxation time. This approach is similar to a closure method used in terrestrial atmospheric turbulent transport (Lewellen 1977). When this is substituted in the equation for < Z >, a little manipulation results in a damped wave equation for the mean concentration. Brandenburg, Kapyla & Mohammed (2004) did extensive comparisons with numerical simulations of passive scalars in mildly compressible turbulence (rms Mach number ~ 0.2) and found good agreement with this model for the time evolution of the spreading size and the non-Gaussianity (kurtosis) of < Z >.

The moment approach can derive the variance of the abundance distribution directly from Equation 1 by writing the velocity, abundance, and source fields as the sum of mean and fluctuating parts (e.g., Z = < Z > + z), multiplying the resulting equation for z / t by z, and then ensemble averaging to obtain

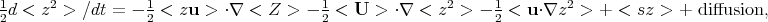(4)

where s is the fluctuating part of the source term (< s > = 0). The first term on the right shows how the scalar flux (< zu >) interacts with any large-scale gradient in the abundance, increasing variance if < zu > is proportional to a mean gradient (as in Equation 3). This is analogous to how stellar orbit diffusion in the presence of a radial gradient produces fluctuations in the stellar abundances. The second term indicates that any gradient in the mean square fluctuations will be advected with the mean flow (e.g., radial flows or infall).

The third term in Equation 4 shows how turbulence can affect a concentration variance even with no gradient in < Z >, zero mean velocity, and without diffusion. Writing this term as < ⋅ (uz²)> - <( ⋅ u)z²> shows that it consists of the mean divergence of the flux of scalar variance, as might be expected, minus a term that is only nonzero in the presence of compressibility. Differentiation and ensemble averaging commute, so the first term of these two is zero for a homogeneous fluid because ensemble averages do not depend on spatial position. The fourth term represents the net production of scalar variance by the fluctuating nucleosynthetic sources. "Diffusion" in this context is shorthand for the fairly complex set of second-order derivatives involving mass diffusion at the molecular level.

As a simple illustration, assume there are no large scale flows and the abundance is linear in galactocentric distance with constant of proportionality G. For a general gradient term, we would have the triple correlation whose closure is discussed by Blackman & Field (2003) and Brandenburg, Kapyla & Mohammed (2004). Then we can also derive an equation for the correlation < zu > by multiplying Equation 1 by u and ensemble averaging. The result is, for <u> = 0,

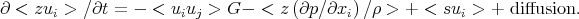(5)

The first term on the right, which is <u²> G for an isotropic velocity field, represents the production of correlations by interaction of the velocity fluctuations with the mean metallicity gradient. We can assume that we are given some steady-state isotropic turbulent velocity field so that <u²> is constant. The second term on the right, often called pressure scrambling, is a serious closure problem for compressible turbulence. The source term is important if the metals come from young stars whose formation is associated with the turbulence itself, but for Type I supernovae or any other source that has time to decorrelate from the flow, <su> = 0. This indicates the importance of using a consistent model for the formation of metal-producers from the turbulent field. Equations 4 and 5 can now be solved to give the evolution of the standard deviation of the abundance distribution for a particular velocity and source field.

If we neglect pressure scrambling in Equation 5 and the compressibility term in Equation 4, and also replace the triple correlation term with a simple gradient-diffusion closure, then the result would show that the concentration fluctuation variance increases <u²> G² t², even in the absence of sources. The turbulence is transporting high-z gas into low-z gas (and vice versa) due to the existence of the gradient. Obviously, after some time the large fluctuations imply steep gradients at very small scales, and so the microscopic diffusion term will cause the variance to level off. In addition, the gradient itself will be washed out by the turbulence unless there is some mechanism continually producing it. Without a sustained mean gradient, such equations could be used to understand how the variance in elemental fluctuations should decrease with time under the action of only advection and diffusion, giving a simplified model to understand the numerical decay results of de Avillez & Mac Low (2002). With some assumed closure for the source terms, or with prescribed velocity field statistics, the solution of Equation 4 would show how the abundance variance depends on the source rate.

2.4. How Do The Metals Enter the Flow?

The source terms in the transport equations depend on how the metals in expanding supernovae and superbubbles are released into the turbulent background. This is not a trivial problem, as discussed by Tenorio-Tagle (1996). Simulations of superbubbles (Korpi et al. 1999) and supernova remnants (Balsara et al. 2001) expanding into a turbulent ISM may provide guidance. Some metal-producing outflows should be jet-like, leading to the release of metals by shear flow along the walls of a chimney. Begelman & Fabian (1990) and Slavin, Shull & Begelman (1993) proposed that such turbulent layers could mix hot and warm gas, but they could just as well mix freshly-produced metals. Tenorio-Tagle (1996) suggested that superbubbles blow out of the disk and rain down metal rich droplets that break apart by Rayleigh-Taylor instabilities. This process could disperse metals over several kpc in the disk with no assistance from disk turbulence.

These processes are also relevant for the redistribution of elements ejected by galactic blowout into the intergalactic medium (IGM). Several papers (e.g., Ferrara et al. 2000, Aguirre et al. 2001 and references therein) have noticed that it is difficult to mix metals on scales comparable to the mean distance between galaxies, requiring an additional (unknown) mechanism. Turbulence in the IGM could provide such a mechanism.

2.5. Turbulent Concentration of Dust Grains

The advection of the grains by turbulent gas can lead to spatial clustering relative to the gas, and to a spatially inhomogeneous dust-to-gas ratio. The degree of segregation depends on the grain size. Local variations in grain-grain velocities affect grain growth and shattering. Early estimates for the efficiency of this process were given by Cameron (1973), Burke & Silk (1976), Scalo (1977), and Draine (1985), but the conception of how grain advection occurs differs greatly in these papers. More rigorous derivations, aimed at grain collisions in protostellar disks but also applicable to the ISM, were given by Völk et al. (1980) and Markiewicz, Mizuno & Völk (1991).

Recent work has been directed toward trapping grains in protoplanetary disks by anticyclonic vortices (e.g., Bracco et al. 1999), which can persist for many turnover times. Large grain concentrations can result, accelerating the formation of planetesimals. Grains might also become trapped in the general ISM because of drag forces, as proposed by Falgarone & Puget (1995).

A review of experiments and simulations on turbulent gas-grain segregation was presented by Fessler, Kulick & Eaton (1994). More recent theoretical investigations (e.g., Sigurgeirsson & Stuart 2002, Lopez & Puglisi 2003) have demonstrated several interesting properties of this clustering. All of this work relies on synthetic velocity fields because inertial particle advection in real turbulent flows would require resolution much finer than the dissipation scale.

Nevertheless, the essential physics of particle drag is becoming more clear. The particle motion is dissipative even if the advecting flow is incompressible, and hence, dissipationless (Balkovsky, Falkovich & Fouxon 2001). This leads to simplified treatments in which the Stokes drag effect is modeled as a small compressible component to the velocity field of the inertial particles. A detailed study of inertial particle dynamics in incompressible flows (Bec et al. 2003) shows that particles smaller than a critical size form fractal clusters whereas larger sizes fill space with a nonuniform density. An extension to highly compressible flows is desirable.

The motion of charged dust grains in anisotropic magnetohydrodynamic (MHD) turbulence was considered by Yan & Lazarian (2002), who made a distinction between the directions parallel and perpendicular to the field. Grains with a gyration time around the field that is shorter than the gas drag time will follow the turbulent field fluctuations in the perpendicular direction. Yan & Lazarian (2003b) calculated the acceleration of charged grains that resonate with MHD fluctuations.

2.6. Turbulent Washout of Radial Abundance Gradients

Another reason to study stirring by interstellar turbulence is to understand the origin of galactic radial abundance gradients (Carraro et al. 1998, Hou et al. 2000, Rolleston et al. 2000). Models typically account for these gradients using a radially dependent timescale for infall and star formation (e.g., Chiappini et al. 2001). A problem is that turbulence should reduce large-scale gradients, so studies of this turbulent washout could give an estimate of the timescale on which the gradient must be replenished. Order of magnitude estimates along the lines of those mentioned in Section 2.2 indicate replenishment timescales larger than characteristic infall times, suggesting that contributions from a radially dependent stellar initial mass function (IMF) or other effects are not required.

A peculiar abundance gradient has been observed in the outer Galaxy, where clusters (Twarog et al. 1997) and Cepheids (Caputo et al. 2001, Andrievsky et al. 2002, Luck et al. 2003) suggest a sudden decrease in metal abundance by about 0.2 dex setting in at 10 kpc. This discontinuity appears over a radial distance less than 1 kpc. It is hard to see how such a feature could survive turbulent washout for more than 10⁸ years using timescale arguments of the type summarized earlier. Either we are missing something fundamental about turbulent transport (e.g., maybe differential rotation or magnetism suppress turbulent motions in the radial direction), or this metallicity near-discontinuity does not really exist.