7. HEATING

Some heating is always expected in the central regions of clusters. Examples are supernovae (Silk et al. 1986, Domainko et al. 2004), an active central nucleus (Bailey 1982, Tucker & Rosner 1983, Pedlar et al. 1990, Tabor & Binney 1993, Binney & Tabor 1995) and many more recent papers cited in Sec 7.2 - 7.5), conduction (Takahara & Takahara 1979, Binney & Cowie 1981, Stewart et al. 1984, Friaca 1986, Bertschinger & Meiksin 1986, Rosner & Tucker 1989) and many more recent papers cited in Sec 7.1).

A problem with heating the gas is that the cooling rate is proportional to the density squared whereas most heating processes are proportional to volume. This tends to make the gas unstable and means generally that the cooler denser gas will carry on cooling while hotter surrounding gas heats up. The gas appears to cool by about a factor of three and then stop cooling. A mechanism to do that is not obvious, since the gas does not appear to be piling up at the lower temperature. Indeed it seems that the gas temperature profile is "frozen" and has been so for some Gyrs (Bauer et al. 2005).

The profile of t_cool is similar in many clusters with a common central minimum value for t_cool of about 200 Myr (Fig. 6). This strongly suggests that heating is continuous, at least on timescales of 10⁸ yr or more and is spatially distributed. Moreover, no shock waves are apparent in these regions so any mechanical energy injection must be subsonic.

Brighenti & Mathews (2003) (see also Ruszkowski & Begelman 2002) provide several 1D simulations of a cluster core in which various levels of heat are injected at various radii. The results which best fit the temperature profile of a real cluster are those without heating. This demonstrates that a heating model is not entirely straight-forward.

Some authors use a combination of processes. Although several are operating in any cluster, it is unlikely that they have similar weight, especially when it is recalled that the cooling flow problem exists in objects ranging from elliptical galaxies, through groups to the most massive clusters. It applies to a range of about 100,000 in X-ray luminosity and over 15 in temperature. We are therefore seeking a wide ranging, quasi-continuous, gentle, distributed heating process

We now consider conduction and AGN heating in detail before discussing other models.

7.1. Heat conduction

The outer cluster atmosphere beyond the cooling radius represents a vast reservoir of thermal energy. Conduction can transfer heat into the cooler central regions. The rate of conduction is however highly uncertain due to the presence of magnetic fields which are probably tangled.

Most workers have adopted Spitzer (Spitzer et al. 1962) conductivity (_S T^5/2), which is appropriate for an unmagnetized gas, and then assumed a suppression factor f. Narayan & Medvedev (2001) suggest that f is about 1/5 since field lines wander away from each other exponentially when tangled (see Tribble 1989 for another discussion).

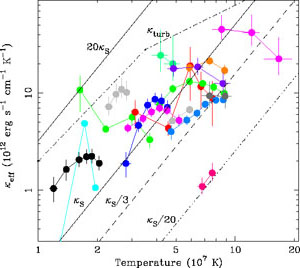Figure 17. The coefficient of electron thermal conduction that would be required to balance X-ray cooling in the cores of a sample of clusters of galaxies. These data are derived by measuring a mean temperature and density as a function of radius and calculating the conduction coefficient to cancel radiative cooling. Each color is a different cluster and each point is a measurement at various radii. The lines are prediction for the magnetic field free conduction coefficient of Spitzer et al. (1962). It is unclear what to expect for the effective conductivity in a cluster of galaxies with a complex magnetic field topology (see text), but it would probably be below the Spitzer value. These results probably indicate the conduction is not strong enough to cancel cooling by itself, but the value required curiously happens to be within an order of magnitude of the canonical value.

Comparison with the data initially looked promising (Zakamska & Narayan 2003, Voigt et al. 2002) then under further inspection ruled it out (Kim & Narayan 2003a, Voigt & Fabian 2004). Voigt et al. (2002) (see also Kaastra et al. 2004 and Voigt & Fabian 2004) used the density and temperature profiles to deduce the heat transfer rate within the gas and thus the effective conductivity _eff required. For several high temperature clusters, _eff < _S , but for clusters where most of the gas is below 5 keV then _eff > _S. Then seems unlikely, however, but this may be possible (Cho & Lazarian 2004).

Cho et al. (2003) proposed that turbulent conduction might work, whereby large subsonic eddies cause heat to be transferred in radius. This does appear to operate fast enough to explain the data (Kim & Narayan 2003a, Voigt & Fabian 2004) provided the gas is highly turbulent. We shall return to the issue of turbulence later when discussing heating by the central radio source (Section 7.2).

We note that conduction as a solution has a fine tuning problem (Nulsen et al. 1982, Bregman 1988). If the gas starts out isothermal, then either the gas cools in which conduction cannot stop it (conduction has a steep positive temperature dependence) or conduction does work and there is no cool gas. How a profile resembling a cooling flow would occur is difficult to understand.

7.2. Heating by a central radio source

Most central cluster galaxies where t_cool in the surrounding gas is less than a few Gyr have a nucleus radio source (Burns 1990). The radio luminosity of these sources has a wide range from the powerful FR II objects Cygnus A and 3C295 to weaker FR I objects such as M87. ROSAT HRI data clearly showed that the FR I lobes of 3C84, the central radio source in the Perseus cluster, have displaced the ICM and so are strongly interacting there (Böhringer et al. 1993). The higher spatial resolution of Chandra has revealed further details of that source (Fabian et al. 2000, 2003a, 2005b) and enabled the discovery of many more, similar, interactions.

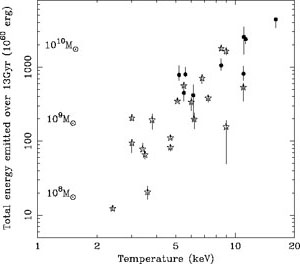Figure 18. The total heating power required to balance radiative cooling a sample of cooling-flow clusters over a Hubble time. The left hand side also indicates the mass of the black hole required if ten percent of its rest mass were applied directly into heating the ICM. Figure adapted from Fabian et al. (2002).

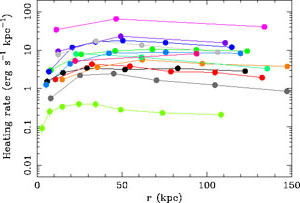Figure 19. The instantaneous heating rate required as a function of radius for a sample of massive cooling-flow clusters. These results indicate that the heating has to be spatially distributed over a substantial physical volume. Figure adapted from Voigt & Fabian (2004).

7.2.1. Overview of radio bubbles

Holes in the X-ray surface brightness coincident with radio lobes are commonly seen and generally referred to as radio bubbles. They are presumed to be relatively empty of normal thermal gas (see limits by Schmidt et al. 2001) and mostly filled with a plasma consisting of relativistic electrons, protons and magnetic field. Striking examples apart from in the Perseus cluster are seen in Hydra A (McNamara et al. 2000); A2052 (Blanton et al. 2001); Centaurus (Fabian et al. 2000); M87 (Young et al. 2002, Forman et al. 2003); A2597 (McNamara et al. 2001, Clarke et al. 2005) and many more (Birzan et al. 2004, Dunn & Fabian 2004, Dunn et al. 2005).

Sometimes outer bubbles are seen (the NW one in the Perseus cluster was first seen in images from the Einstein Observatory, Fabian et al. 1981, Branduardi-Raymont et al. 1981) which are considered to be ghost lobes. Synchrotron and other losses have depleted the population of radio-emitting electrons to the extent that they are not detectable in the radio (particularly not at high frequencies) yet the other electrons, protons and magnetic field in the cavities still exclude the X-ray emitting thermal gas. Weak, low-frequency radio emission pointing at the outer bubbles in the Perseus cluster supports this hypothesis (Fabian et al. 2002).

The bubbles discussed so far have radii from about 1 to 15 kpc. Recently, giant bubbles of radius 100 kpc have been found 100-200 kpc from the centers of the Hydra-A nucleus (Nulsen et al. 2004) and in MS0735.6+7421 (McNamara et al. 2005), and some bubbles with little energy (e.g. Blanton et al. 2004). The minimum energy of a bubble can be estimated from its volume V and surrounding pressure P as E_bubble = PV. If the interior pressure is entirely relativistic in gas with a ratio of specific heats of 4/3 then E_bubble = 4PV. The energies are significant for typical bubbles (Birzan et al. 2004) and exceed 10⁶¹ erg for the giant bubbles.

7.2.2. The simple theory of bubbles

Bubbles from radio sources were first predicted by Gull & Northover (Gull & Northover 1973) and studied analytically before the Chandra/XMM-Newton era by Churazov et al. (2000 2001) (see also Soker et al. 2002) and simulated by Heinz et al. (1998). They are inflated by jets from the nucleus and typically form in pairs either side of the nucleus and seemingly attached to the nucleus. If a jet of power L steadily inflates a bubble of radius R then, after an initial supersonic phase and assuming radiative losses are negligible, the bubble expansion with time t follows from the conservation of energy as Lt = P V P R³. Thus R t^1/3 and the expansion speed of the bubble v_bubble t^-2/3. The bubble is of much lower density than its surroundings so is buoyant and rises at a velocity close to the local gravitational free-fall value v_grav. When v_bubble drops below v_grav the bubble detaches from the jet and rises. A new bubble then forms if the jet remains powered.

A simple estimate of the power injected into the bubbles can be obtained by dividing E_bubble by an estimate of the age of the bubble, which can be obtained from the above scaling (say, R/v_grav) (Birzan et al. 2004, Dunn & Fabian 2004, Dunn et al. 2005). These are typically several orders of magnitude higher than the inferred radio luminosity of the jets and nucleus showing that the radio luminosity is a poor guide to the power of a jet. Such radio jets and lobes can have a radiative efficiency (ratio of observed synchrotron luminosity to mechanical power) as low as 10^-3 or even 10^-4. This, together with time variability of the jets, indicates that the very poor correlation between the radio power of the central source in a cluster and the heating power (Voigt & Fabian 2004, Kaastra et al. 2004) does not necessarily imply that the mean jet power does not correlate well.

The power of the jets is mostly sufficient to offset radiative cooling in the cluster core provided it is steady. Birzan et al. (2004) did however note that it is insufficent in some objects. This could indicate that radio source heating is not a general process or that it can vary by factors of a few on the bubbling timescale, which ranges between ~ 5 Myr and ~ 50 Myr. This timescale is still shorter than the inner radiative cooling timescale which is typically 100-300 Myr.

A further problem they raise is that bubbles were only found in 10 per cent of the clusters they examined, so they either do not occur in many clusters or if they do then they do not occur often. This result could however be a selection effect from the examination of a sample of clusters mixed in type (i.e. whether the cooling flow problem applies to that cluster or not) and signal-to-noise. A simple inspection by ACF of Chandra images of the 30 per cent of the 55 brightest clusters in the Sky listed by Edge et al. (1992) which have central t_cool < 5 Gyr shows that all but one have clear bubbles, so we suspect that bubbles are indeed common enough to be a viable ingredient in the solution to the cooling flow problem. A more detailed analysis of the issue by Dunn et al. (2005) shows that at least 75 per cent of the cluster cores needing heating have bubbles. This means that the duty cycle of bubbles is such that they are (detectably) present for 75 per cent of the time.

Finally, before examining numerical simulations and then the heating mechanism in detail, we note that the total energy required to stave of cooling for several Gyr in a luminous cluster implies a large central black hole mass (Fabian et al. 2002; assuming a mass-to-energy conversion effiency of 10 per cent). Fujita & Reiprich (2004) compared black hole masses predicted by the velocity dispersion relation (Tremaine 2002) and found that they often fall short of what is required. However for the very few systems where the mass has been measured (e.g. M87) there is no problem. Perhaps the conclusion here would be that massive black holes in cluster cores lie above the M_BH - relation for lower mass galaxies.

7.2.3. Numerical simulations of radio bubbles

Many groups have now carried out numerical hydrodynamical simulations of the behaviour of bubbles in the ICM (Brüggen & Kaiser 2001, Quilis et al. 2001, Brüggen & Kaiser 2002, Brüggen 2003, Basson & Alexander 2003, Omma & Binney 2004, Omma et al. 2004, Ruszkowski & Begelman 2002, Ruszkowski et al. 2004a, Ruszkowski et al. 2004b, Robinson et al. 2004, Vecchia et al. 2004, Reynolds 2005).

Most have been 2D or 3D and use the FLASH or ZEUS codes (see Gardini & Ricker 2004) for a brief discussion and comparison of many of the simulations). Several assume that the surrounding gas is isothermal. Many produce bubbles which are very unstable (to Rayleigh-Taylor and Kelvin Helmholtz instabilities depending on the motion of the bubble at the start of a run) and collapse once they have risen more than their own height, which is most unlike the observed bubbles. Indeed most simulated bubbles do not look like the observed ones.

Several of the early simulations relied on the dragging out of cooler gas from the smallest cluster radii by the bubbles as the explanation of why so little cool gas is seen in real clusters. This explanation however only works over the lifetime of the cluster (say 5 Gyr) if the cooler gas is dragged out beyond the cooling radius (i.e well beyond 100 kpc), otherwise it either falls back in or mixes in and reduces the cooling time of gas just beyond the center. A catastrophic cooling flow is only being postponed for a while. Although this explanation can work temporarily it cannot provide a comprehensive solution.

When heating is estimated in simulations it is often unclear what it is due to. Some work is done by the buoyant bubbles rising and the sinking of cooler gas. This is the heating mechanism of the 'effervescent heating' approach of Begelman (2001) (see also Ruszkowski et al. 2004a). P d V work is done as the bubbles are made in the first place. That energy presumably propagates as a sound wave and need not be dissipated locally unless shocks are involved or the ICM is viscous.

Heating by a mixture of weak shocks (at small radii) and viscous damping of sound waves (at larger radii) has been proposed by Fabian et al. (2003b) on the basis of the ripples seen in deep Chandra images of the Perseus cluster (see also Forman et al 2004 for a discussion of ripples in the Virgo cluster). Viscosity has been included in simulations by Ruszkowski et al. (2004a, b) and by Reynolds et al. (Reynolds 2005) and appears to dissipate 20-30 per cent of the P d V energy from the bubbles. Transport of the energy by sound waves and dissipating it over a lengthscale of 50-100 kpc provides a fairly gentle and distributed source of heat. The bubbles in a viscous medium also better resemble the observed ones (Reynolds 2005).

Fujita & Suzuki (2005) and Mathews et al. (2005) argue that strong sound waves will shock and heat the innermost region and not deposit energy further out where it is needed. However a very deep image of the Perseus cluster (Fabian et al. 2005b) shows that the shock (Fig. 15) is isothermal. This may indicate that thermal conduction operates at least within the inner parts of the cool region to share the energy released by the bubbling process.

7.3. Is the ICM turbulent?

Several workers (Cho et al. 2003, Inogamov & Sunyaev 2003, Chandran 2004, Fujita & Reiprich 2004) suggest that the ICM is turbulent. Such motions can transport heat and the dissipation of the turbulence is itself a source of heat. Schuecker et al. (2004) have measured brightness and temperature fluctuations in the Coma cluster (which is not a cooling flow cluster). Vogt & Ensslin (2004) have determined a limited turbulent-like spectrum in the Faraday Rotation Measures of the Hydra cluster core. Ensslin (2005) have extended their work to predict velocities and length-scales for the turbulence in a number of cool core clusters. They argue that a small-scale turbulent dynamo is maintaining magnetic fields and that turbulent dissipation can balance radiative cooling.

Contrary indications have been identified (Fabian et al 2003b) in the highly extended, and often linear, optical filaments in the Perseus (Conselice et al. 2000) and other clusters (e.g A1795, Cowie et al. 1983; Centaurus, Crawford et al. 2005). Such filaments have coherent velocity fields and small velocity widths (Hu et al. 1985, Crawford et al. 2005, Hatch et al. 2005b) so must be relatively old (perhaps 100 Myr) and in thermal pressure equilibrium with the surrounding ICM. The optical surface brightness of such filaments translates to a thickness of the emission regions of less than a pc. If the ICM is turbulent and pushing on a filament, it will respond after interacting with its own column density which means a kpc or so of ICM, given the thousandfold higher density in the filament. This is only a few arcsec in nearby clusters so the apparent linear nature of the filaments would soon be destroyed by a fully turbulent ICM. They may however reflect streamlines and could have been drawn out by the motion of bubbles. Note the similarity of the horseshoe-shaped filament in the Perseus cluster to that of streamlines behind rising water bubbles; see Fig. 184 in van Dyke (1982) and discussion by Fabian et al. (2003b)

The inner ICM in clusters with significant linear filaments may therefore have subsonic random flows, particularly radial behind bubbles. Whether this is turbulence depends on how turbulence is defined. It does not resemble fully-developed hydrodynamical turbulence (see Fig. 186 in van Dyke 1982) but is not dissimilar from flows in some magnetohydrodynamical simulations (e.g. Schekochihin et al. 2004).

What is unclear is the driving mechanism for turbulence in a cluster core. A subcluster merger may well have made the Coma cluster ICM turbulent, but such mergers will not have strongly affected the dense core cluster under discussion here (but see Fujita & Reiprich 2004). Driving turbulence into the dense core will require considerable energy. Rising radio bubbles are a possible driver but whether their motion leads to a turbulent cascade of energy to much smaller scales must be determined. The viscosity of the ICM may play a key role in this issue.

The abundance gradients seen at the centers of many cool core clusters provides a further constraint on turbulence and diffusion. Rebusco et al. (2005) have modelled the production and maintenance of the gradient in the Perseus cluster and find a diffusion coefficient D ~ v 2 × 10²⁹ cm² s^-1. Graham et al. (2005) have carried out a similar analysis on the more abundance-peaked Centaurus cluster to obtain a value of D ~ 5 times smaller.

7.4. Multiphase flows

Large scale global flows have been considered that transfer significant thermal energy from one region of the cluster to another. Matthews et al. (2003, 2004) have discussed flows which move in both radial directions. To be long lived, both mass and energy must be supplied to the inflowing gas over a large volume. The energy is assumed to be derived from bubbles.

Fabian et al. (2003a) considered a multiphase flow in which outer denser blobs fall inward and mix with inner, cooler blobs, thereby tapping the extended gravitational potential. Unless there is some outflow or cooling, however, mass builds up near the cluster center.

7.5. Role of Magnetic Fields and Cosmic Rays

A cooling flow will amplify tangled magnetic fields in the intracluster gas (Soker & Sarazin 1990). Magnetic fields in the general ICM have been found through radio observations of Faraday Rotation (Kim et al. 1991, Clarke et al. 2004). Such observations also show it rising in cool core clusters where the highest values have been found (Carilli & Taylor 2002). The results indicate a roughly cellular structure for the magnetic field of a few kpc (e.g. the Centaurus cluster, Taylor et al. 2002). Such a structure may occur from a spectrum of magnetic fields perhaps due to turbulence (Ensslin 2005). Near the center the magnetic pressure can be 10 per cent of the thermal pressure, perhaps more. An important effect of the magnetic field is that it can dramatically reduce the microphysical transport processes in the ICM.

Cosmic rays are a likely additional component in cluster cores. Relativistic electrons produce the minihalo in the X-ray peaked region of the Perseus cluster (see Gitti et al. 2004 for a theoretical discussion) and may produce a hard X-ray component by inverse Compton scattering (Sanders et al. 2005). The effects of cosmic rays could be important in mediating the flow of mechanical energy in the core.

Cen (2005) notes that a cosmic ray phase can make heated gas thermally stable. A floor temperature of 0.3 times the local ambient temperature is derived if the cosmic ray pressure is 1/3 of the ambient value. This situation is different from the similar factor seen in observations, which applies across the whole cool region, not just locally. Note that gas is not observed to "pile up" at any particular temperature.

If cosmic rays are spread through the core in many small bubbles, then they would be very effective in dissipating the energy in sound waves (Heinz & Churazov 2005). Such bubbles must be small not to be detectable in deep images (eg. Fabian et al 2005b).

7.6. Feedback

If AGN heating balances cooling on timescales of ~ 10⁸ to a few 10⁹ yr then some feedback is needed to prevent either a cooling catastrophe (none has yet been found) or an event heating all the central gas and blowing it out. Bondi accretion onto a central black hole provides a link between the two regions but the radius range from the Bondi radius of say 50 pc to the ICM at 50 kpc is a factor of one thousand. The volume occupied by the black hole and its accretion radius which is required to provide the heating is one part in a billion!

Such numbers emphasize the problem faced by the necessary feedback. Some attempts to model feedback are discussed by Ciotti & Ostriker (2001); Kaiser & Binney (2003); Nulsen et al. (2004), Soker & Pizzolato (2005), Omma & Binney (2004); Binney (2004); Hoeft & Brüggen (2004); Churazov et al. (2005); Pizzolato & Soker (2005). The common occurrence of star formation in the central galaxy and also of giant bubbles shows that any feedback need not be perfect on timescales less than 10⁸ yr. Donahue et al. (2005) study two clusters which show little central temperature drop or central radio source yet have central cooling times of ~ 1 Gyr. Such clusters, which are in the minority, may be recovering from giant outbursts.

7.7. Other heat sources and mechanisms

Cosmic ray heating has been invoked in several models (Colafancesco et al. 2004, Totani 2004). Generally to be effective, the pressure in cosmic rays would have to exceed that of the thermal gas (Loewenstein 1991). Excess ionization by suprathermal electrons could change the spectral appearance of gas in a cooling flow. This has been studied by Oh (2004), who finds that such electrons provide much more heating than ionization, so reverting to the problems raised above by Loewenstein (1991).

Heating by galaxy motions have been revived by El-Zant et al. (2004) (see also Faltenbacher et al. 2005) following early work by Miller (1986). It may be a viable distributed source of heat if the mass-to-light ration of the galaxies passing through the inner regions exceeds 10 (but see Kim 2005).

Dark matter interactions have been discussed by several authors (Qin & Wu 2001, Totani 2004, Chuzhoy & Nusser 2004). Similarities with the solar corona have been discussed by Makishima (2001) and Kaastra et al. (2004). Brüggen & Ruszkowski (2005) discuss that viscous heating, if it occurs in real MHD plasmas, could provide significant heating during structure formation.

One last possibility is that sedimentation acts (Fabian & Pringle 1977). Helium then accumulates at the cluster center (Gilfanov & Sunyaev 1984) possibly explaining the puzzling low metallicity found at the center of some nearby clusters observed with Chandra. The main low temperature cooling gas is then helium rich which can produce much weaker emission lines. Stars formed from helium rich gas will have short lifetimes so avoiding some constraints on the cold mass sink (Fabian et al. 2003c, Ettori & Fabian 2005). Tangled magnetic fields will of course significantly reduce the prospect of any sedimentation.