Not all true global instabilities in disks require a feedback loop. Another class of modes is simply driven from corotation, with trailing waves propagating both inwards and outwards to be absorbed, in stellar disks, at the Lindblad resonances on either side.
Lovelace &
Hohlfeld (1978)
showed that disks are destabilized by a local extremum in
the radial variation of the ratio of surface density to vorticity,
/
|
× v| 
/
(2
2),
or the reciprocal of potential vorticity, and proposed that the
instability created flat rotation curves for which the potential
vorticity is also flat.
Sellwood & Kahn
(1991)
demonstrated that the instability
caused by a ratherinsignificant, narrow, decrease in surface
density, i.e. a "groove", is a global spiral mode.
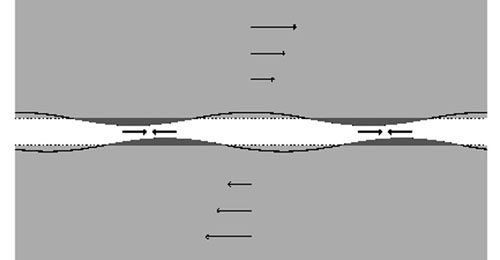
The mechanism is easiest to visualize in a disk without random motion, where small-scale surface density variations are not blurred by epicyclic motions. In this case, a deficiency of stars over a small range of angular momentum creates a groove in the surface density, as shown in the sheared sheet model in the top panel of Fig. 7. The groove itself is unstable because of the gravitational coupling between disturbances on either side. The dark shaded areas in the Figure illustrate regions where small sinusoidal radial displacements of material on each edge have created high density regions where the density was previously low. Disturbing gravitational forces arise from the density excesses, as illustrated, which are directed along the groove if the wavelength is long compared with the groove width. Material that is pulled back loses angular momentum and sinks toward the center of the galaxy, while that which is urged forward gains and rises outwards. Thus each density excess pulls on the other across the groove in such a way as to cause it to grow exponentially, i.e. the combined disturbance on the two sides is unstable. The groove edges need be only steep gradients, not discontinuities. Furthermore, the mechanism is the same, but harder to visualize, in a disk with random motion where the density of stars is depleted over a narrow range of angular momentum.
 |
 |
Figure 7. The top panel illustrates a
groove in the sheared sheet
(Section 3.6) model. The light shaded
region has the full undisturbed disk surface density,
|
The growing disturbance in the groove creates wave-like mass variations along the groove that are effectively growing co-orbiting mass clumps of the type envisaged by Julian & Toomre (1966). Generalizing their apparatus to allow for exponentially growing masses, Sellwood & Kahn (1991) estimated the expected disk response, as shown in the lower panel of Fig. 7 for the parameters Q = 1.8 and X = 2, and low growth rate. The disk supporting response transforms the quite trivial disturbance in the groove into an extensive spiral instability!
Unlike the sheared sheet, the azimuthal wavelength in a full disk can
take on only discrete values,
y =
2
R / m, which
are all unstable, but the one which grows most rapidly is that for which
swing-amplification (Section 3.6) is
the most vigorous, i.e. 1
X 2.5
(eq. 12) in a flat rotation curve. The simulation
shown in Fig. 8 illustrates the scale and vigor
of the mode, which saturates at ~ 20% overdensity because of the onset of
horseshoe orbits at corotation
(Sellwood & Binney
2002).
 |
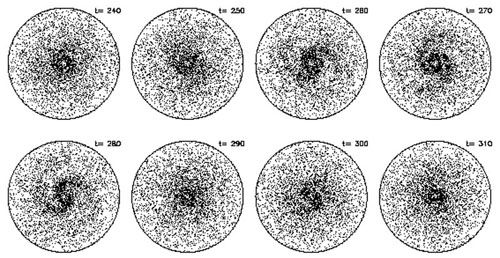Figure 8. The later part of the growth and subsequent decay of an isolated spiral mode in a disc that was seeded with a groove. Disk rotation is counter-clockwise and disturbance forces in this simulation, taken from Sellwood & Binney (2002), were restricted to m = 2 only. |
Lovelace & Hohlfeld (1978) and Sellwood & Kahn (1991) found that almost any narrow feature in the angular momentum density is destabilizing, although the modes of a simple ridge, for example, come in pairs with CR some distance from the ridge center.
Edge modes (Toomre 1981, Papaloizou & Lin 1989) are close cousins of groove modes, and the mechanism can be understood in the same fashion. Density variations on a single edge without a supporting disk response are neutrally stable, but the necessarily one-sided wakes in the massive interior disk add angular momentum to the density enhancements on the edge, causing them to grow.
The eigenfrequencies of the low order bisymmetricmodes of the Gaussian disk vary with decreasing disk mass as shown in Fig. 9, taken from Toomre (1981). Most are cavity modes, but the edge-mode, labelled "mode D" stands out because its growth rate in particular declines more slowly with decreasing disk mass. If the mechanism for both types of mode involves swing amplification, one might expect their vigor to be similarly affected by the rise in the X parameter as the surface density decreases. But the decreased surface density also slows the group velocity while the rapidly declining pattern speed of each cavity mode moves CR farther out in the disk. Thus the growth rates of cavity modes drop more quickly because of the increased travel time for the wave packet to complete the feed-back loop, a factor that is absent for the edge mode.
 |
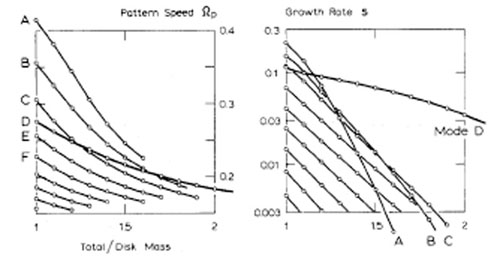Figure 9. The variation of pattern speeds and growth rates for the first few m = 2 modes of the Gaussian disk as the active disk mass is decreased. From Toomre (1981). |
The edge instability requires only a steep gradient in the surface
density, which need not drop to zero.
Toomre (1989)
gave the
condition for instability as "the radial distance over which the disc
density undergoes most of its rapid change should be no larger than
about one quarter of the axisymmetric stability length
crit",
assuming "the disc is massive and cool enough
for vigorous swing-amplification."
Curiously, global bar-forming modes were originallythought to be related the rotational instabilities of uniform-density Maclaurin spheroids of incompressible fluid (Ostriker & Peebles 1973), an idea reinforced by the vigor of the bisymmetric mode of the sharp-edged Maclaurin disk (Kalnajs 1972). Toomre (1981) noted that the instability of such unrealistic galaxy models may be more closely related to the edge mode than to the cavity mode described in Section 4.1.
As the consequence of an edge instability in a realistic galaxy model is to blur the edge, it seems unlikely that galaxy disks can retain unstable density gradients for interestingly long periods. Similarly, the large-amplitude evolution of groove or ridge modes quickly erases the feature that gave rise to them. Nevertheless, the modes have other possible consequences (see Section 7.6).