Despite many decades of effort, no theory to account for the graceful spiral patterns in disk galaxies is widely accepted. Most workers in this field agree that spiral patterns are gravitationally driven variations in surface density in the old stellar disk, as supported by photometric data (e.g. Grosbøl et al. 2004, Zibetti et al. 2009) and streaming motions in high spatial resolution velocity maps (e.g. Shetty et al. 2007).
There seems little doubt that some spiral patterns are tidally driven (e.g. Salo & Laurikainen 1993, Dobbs et al. 2010), while others could be the driven responses to bars (Buta et al. 2009). Although these two ideas may account for a large fraction of the cases (Kormendy & Norman 1979), especially if orbiting dark matter clumps can excite patterns (Dubinski et al. 2008), spirals can still develop in the absence of either trigger, as revealed in simulations.
The idea that spirals could be self-excited oscillations of the stellar disk represents the greatest theoretical challenge. While there is general agreement that gas seems to be essential, no picture seems complete, and current theories disagree on even the lifetimes of the patterns. One idea (e.g. Bertin & Lin 1996), is that spiral features are manifestations of quasi-steady global modes of the underlying disk. Alternatively, they could be short-lived, recurrent transient patterns that originate either from forcing by density fluctuations (e.g. Toomre 1990), or else from recurrent vigorous instabilities (e.g. Sellwood 2000).
A serious obstacle to progress in this area has been the absence of observational discriminants that would favor one of these radically differing viewpoints over the other. The predictions for density variations or gas responses at a single instant are essentially independent of the generating mechanism and do not depend strongly on the lifetime of the pattern. Meidt et al. (2009) attempted to measure radial variations of pattern speeds using a generalization of the method devised by Tremaine & Weinberg (1984a) (see Section 9.5). They reported lower pattern speeds at larger radii, but their measurements still tell us little about spiral lifetimes. However, the velocity distribution of stars in the solar neighborhood (Nordström et al. 2004 and Fig. 1) is most naturally accounted for in the transient picture (see Section 7.6).
7.1. Spirals as Global Modes of Smooth Disks
Simple models of disk galaxies possess many linear instabilities (e.g. Jalali 2007). The bar-forming mode (Section 4) is usually the fastest growing, but it has almost no spirality. These studies are therefore important to understand stability, but even the higher modes are not particularly promising for spiral generation. 7
The "density wave" theory for spiral modes, described in detail by
Bertin & Lin
(1996),
invokes a more specific galaxy model with a sub-maximal
disk that is dynamically cool in the outer parts and hot in the inner
disk. The local stability parameter is postulated to be 1.0
Q
1.2 over most of
the disk and to rise steeply to Q > 2 near the
center. Bertin, Lin, and their co-workers perform a global analysis
using the hydrodynamic approximation (BT08, Section 5.1), which reveals
slowly growing spiral modes under these specific conditions.
The mechanism (Mark 1977) is a cavity mode, having qualitative similarities to that for the bar mode (Section 4.1), but the tightly-wrapped waves are trailing around the entire cycle. The inner turning point is at a Q-barrier: a steeply increasing Q value causes the forbidden zone (Section 3.4) to broaden to the point that in-going short waves get "refracted" into outgoing long waves, which prevents the wave train from reaching the ILR where it would be damped. The long waves then propagate out to near the CR in the Q ~ 1 part of the disk, where they switch back to the shortwave branch with a small degree of amplification. The WASER mechanism (Mark 1976) at this turning point involves a third, transmitted wave that is "radiated" outwards on the short-wave branch, carrying away the angular momentum to excite the mode in the inner disk. Thus the amplifier involves a small "swing" from the long- to the short-wave branch, whereas the bar instability uses a full swing from leading to trailing. This difference, together with their assumption that the disk is sub-maximal (i.e. X > 3 for m = 2, see eq. 12), allows the mode to be slowly growing. Lowe et al. (1994) present a model of this kind to account for the spiral structure of M81.
In order to justify the "basic state" of the disk they require, Bertin & Lin (1996) argued heuristically that rapidly evolving features would have disappeared long ago and that low-growth-rate instabilities in a cool disk, created by gas dissipative processes and star formation, will dominate at later times. They invoked shocks in the gas to limit the amplitude of the slowly growing mode, leading to a quasi-steady global spiral pattern.
The main objection to their picture is that it is likely that such a lively outer disk will suffer from other, more vigorous, collective responses with m > 2 that will quickly heat the disk, as described in Section 7.5, and destroy their postulated background state.
From the early work by Miller et al. (1970), Hohl (1971), Hockney & Brownrigg (1974), James & Sellwood (1978), and Sellwood & Carlberg (1984), N-body simulations of cool, sub-maximal disks have exhibited recurrent transient spiral activity. This basic result has not changed for several decades as numerical quality has improved.
Claims of long-lived spiral waves (e.g. Thomasson et al. 1990) have mostly been based on simulations of short duration. For example, Elmegreen & Thomasson (1993) presented a simulation that displayed spiral patterns for ~ 10 rotations, but the existence of some underlying long-lived wave is unclear because the pattern changed from snapshot to snapshot. Donner & Thomasson (1994) ran their simulations for fewer than 7 disk rotations and the bi-symmetric spiral they observed appeared to be an incipient bar instability. Zhang (1996, 1998) adopted a similar mass distribution and also reported long-lived patterns in her simulations. The author has attempted to reproduce her results, and indeed obtained similar bi-symmetric features, but they appear to be the super-position of several waves having differing pattern speeds.
Sellwood & Carlberg (1984) stressed that patterns fade in simple simulations that do not include the effects of gas dissipation; the reason is the disk becomes less responsive as random motion rises due to particle scattering by the spiral activity (Section 10), which is therefore self-limiting. They also demonstrated that mimicking the effects of dissipative infall of gas, such as by adding fresh particles on circular orbits, allowed patterns to recur "indefinitely." Later work (e.g. Carlberg & Freedman 1985, Toomre 1990) has shown that almost any method of dynamical cooling can maintain spiral activity, as also happens in modern galaxy formation simulations (e.g. Agertz et al. 2010).
Thus the transient spiral picture offers a natural explanation for the absence of spiral patterns in S0 disk galaxies that have little or no gas; maintenance of spiral activity requires a constant supply of new stars on near-circular orbits. Other pieces of indirect evidence that also favor the transient spiral picture are reviewed in Section 10.
7.3. Spirals as Responses to Density Fluctuations
Goldreich & Lynden-Bell (1965b) and Toomre (1990) suggested that a large part of the spiral activity observed in disk galaxies is the collective response of the disk to clumps in the density distribution. As a spiral wake is the collective response of a disk to an individual co-orbiting perturber (Julian & Toomre 1966), multiple perturbers will create multiple responses that all orbit at different rates. The behavior of this polarized disk reveals a changing pattern of trailing spirals, which can equivalently be regarded as swing-amplified (Section 3.6) noise. 8
Toomre & Kalnajs
(1991)
studded the amplified noise that arose in their N-body
simulations of the sheared sheet. The massive particles themselves
provoke spiral responses with an amplitude proportional to the input
level of shot noise, caused by density variations in the distribution
of randomly distributed particles. Comparison of their expectations
with linear theory predictions revealed that the simulations were
livelier than they expected, by a factor
2, apparently from a
gradual build-up of correlations between the mean orbital radii of the
particles.
This could be a mechanism for chaotic spirals in very gas rich discs, where a high rate of dissipation may be able to maintain the responsiveness of the disc (Toomre 1990) while the clumpiness of the gas distribution may make the seed noise amplitude unusually high. However, it seems likely that spiral amplitudes (e.g. Zibetti et al. 2009) are too large to be accounted for by this mechanism in most galaxies. Also, the spiral structure should be chaotic, with little in the way of clear symmetry expected.
7.4. Non-linear Spiral Dynamics
Tagger and his co-workers (Tagger et al. 1987, Sygnet et al. 1987, Masset & Tagger 1997) suggested that global modes in stellar disks could be coupled through non-linear interactions. They proposed that wave 1 excites wave 2 through second-order coupling terms that are large when CR of wave 1 lies at approximately the same radius as the ILR of wave 2. Conservation rules require a third wave such that m3 = m1 ± m2; i.e. most likely an axisymmetric wave (m3 = 0) if m1 = m2. Many examples of multiple waves in N-body simulations have been reported with remarkable coincidences for the radii of the main resonances.
Fuchs et al. (2005) developed a similar argument for waves in the sheared sheet. They found that amplified trailing waves could excite fresh leading waves in their second-order theory. They proposed this mechanism as an alternative source of the amplitude excess noted above in the simulations by Toomre & Kalnajs (1991), and they speculated that the same mechanism may also account for the larger than expected amplitudes of spirals in global N-body simulations (see Section 7.5). As both this mechanism, and that discussed in the previous paragraph, employ terms that are second-order in the perturbation amplitude, they will become important only when features are strong.
Patsis et al. (1991) attempted to construct, by orbit superposition, self-consistent steady spiral waves of finite amplitude to match the observed non-axisymmetric patterns in specific galaxies. They experienced great difficulty in finding solutions near CR, and suggested that either this resonance or the 4:1 resonance 9 marks the outer radius of the spiral. Their finding is not unexpected for two reasons: (a) the dispersion relation for steady, tightly-wrapped, small-amplitude waves (Fig. 4) predicts a forbidden region around CR for all Q > 1, and (b) the non-linear dynamics of orbits in barred potentials (see Section 9.3) finds only chaotic orbits near CR, which are unfavorable to self-consistency as Patsis et al. (1991) found. It should be noted that the difficulty of finding a self-consistent solution near CR is a direct consequence of their assumption of a steady wave pattern; transient waves do not suffer from this problem (Fig. 5) and rapidly growing groove modes (Section 6) have peak overdensities at CR.
Tsoutsis et al. (2009) and Athanassoula et al. (2009) suggested that spirals in barred galaxies could be created by the slow migration of stars along Lyapunov manifold tube orbits emanating from the unstable Lagrange points at the ends of the bar. 10 The ambitious hope of these preliminary papers is for an ultimate unified picture for the co-existence of bars, spirals and rings, all having the same pattern speed.
7.5. Spirals in Global N-body Simulations
Sellwood & Carlberg (1984) and Sellwood (1989b) reported that their global simulations manifested more vigorous spiral activity than was consistent with amplified shot noise. A brief summary of some further results to support this claim is given here, and will be described more fully elsewhere.
As noted in Section 4.1,
Toomre (1981)
predicted the half-mass
Mestel disk to be globally stable to small-amplitude disturbances.
Thus N-body simulations of this disk should exhibit no activity in
excess of the inevitable swing-amplified shot noise.
Fig.10 reveals that this is not the case. The
ordinate shows the largest value of
=
/ from m =
2 disturbances in a sequence of simulations with increasing numbers
of particles. The unit of time is Ri /
Vc, where Vc Ri is the
center of the inner angular momentum cut out. Thus the orbit period
at this small radius is 2
.
 |
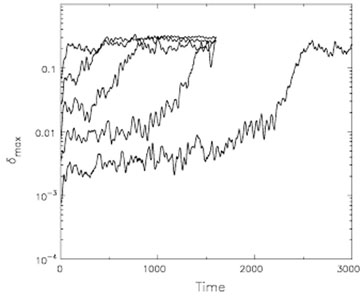Figure 10. The time evolution of the peak
overdensity in a series of simulations of the half-mass Mestel disk
with different numbers of particles. The model was predicted by
Toomre (1981)
to be globally stable. The ordinate shows the maximum values of
|
At t = 0,
N-1/2, as appropriate for shot noise,
and swing-amplification causes an almost immediate jump by a factor of
a few for all N. When N = 5 × 104,
amplified noise causes
~ 20% overdensities almost immediately. For larger N the
amplitude eventually rises to similar values in later evolution, once
the inner disk has developed a pronounced bar. But for the largest
two values of N shown, a period of slow growth occurs after the
initial swing-amplified surge, offering tentative support for the
linear theory prediction of global stability, with the slow growth
perhaps arising from the gradual development of particle correlations
as described by
Toomre & Kalnajs
(1991).
Even in these cases, however, the amplitude rises more rapidly once
2%.
Thus even in these highly restricted simulations, spiral activity
always exhibits runaway growth - albeit more and more delayed as
N is increased - behavior that is quite clearly not in accord with
linear theory predictions. The rapid growth once
2%
suggests that the behavior has already become non-linear in some
respect at this modest amplitude. Note that the largest number of
particles, N = 5 × 108, is within a factor of 100
of the number of stars in a real galaxy disk, where in reality the mass
distribution is far less smooth, owing to the existence of star clusters
and giant gas clouds.
7.6. A Recurrent Instability Cycle?
Sellwood & Lin (1989) reported evidence for a recurrent instability cycle in their simulations of a very low-mass disk. They observed that each spiral pattern created substantial changes to the distribution of particles at the Lindblad resonances, which they suspected created conditions for a new global instability of the groove mode kind (see Section 6). They explicitly demonstrated that the later features were indeed true instabilities, since when they continued a parallel simulation after randomly shuffling the particles in azimuth at some moment, the pattern speed of the next mode to appear was the same as that in the original simulation that had not been interrupted. 11 Thus, each coherent wave leaves behind an altered DF that apparently provokes a new instability.
The runaway growth in the larger N models shown in
Fig. 10
is not caused by a single unstable mode, but appears to be a
succession of separate coherent waves, each having a lower rotation
rate and reaching a higher amplitude than the last.
Sellwood (2000)
reported similar behavior in lower-N simulations, and demonstrated
that one of the waves did indeed cause strong scattering at the ILR.
It should be noted that resonance scattering is a second-order effect,
but the evidence shown in Fig. 10 suggests that
it becomes important at a relative overdensity of just
/
~ 2%. Exactly how the demise of one mode creates the conditions
for the next instability remains unclear, however.
Since the only evidence for this behavior came from a (well-tested) N-body code, it seemed best not to pursue the idea further until supporting evidence could be found. Sellwood (1994) therefore expressed the hope that evidence of resonance scattering could be found in the HIPPARCOS measurements of the local stellar kinematics. The publication of the GCS with distances and full phase-space motions of ~ 14000 F & G dwarf stars (see Fig. 1) enabled Sellwood (2010) to show that the so-called Hyades stream is in fact caused by scattering at a recent ILR.
This very recent evidence supports the idea that spirals in the local Milky Way, and presumably elsewhere, do in fact behave as the simulations had indicated. Further work is required to expose the details of the recurrence mechanism. However, it now seems misguided to search for a spiral instability as some devious sort of cavity mode in a smooth disk; i.e. the assumption of a featureless DF may have thrown the spiral baby out with the bathwater!
7 Korchagin et al. (2005) calculated essentially gas-dynamical modes for models of specific galaxies, and argued that the shapes of one, or more, of the lower-order modes could be matched to the observed spiral pattern. However, it is unclear that rapidly growing, linear modes can be seen for long at finite amplitude before non-linear effects will change their appearance, and it seems even less likely that two modes with different growth rates should have similar large amplitudes at the time a galaxy is observed. Back.
8 Cuzzi et al. (2010) found evidence for similar behavior within Saturn's A ring. Back.
9 The resonance condition (eq. 5) for a pure cos(mθ) potential variation also implies frequency commensurabilities at multiples of m. The small denominators that characterize the principal resonances (BT08, Section 3.3.3) arise at these "ultraharmonic resonances" only for non-circular orbits. A new family of orbits appears at the 4:1 resonance that closes after 4 radial oscillations (see Section 9.3 and Sellwood & Wilkinson 1993). Back.
10 Interestingly, this idea harks back to the old "garden sprinkler" model for spirals proposed by Jeans (1923) (see also Jeans 1929, fig. 55 & pp. 357-360). Back.
11 This behavior is inconsistent with the non-linear mode coupling ideas discussed in Section 7.4. Back.