5. GALAXY BIAS

It was realized decades ago that the spatial clustering of observable galaxies need not precisely mirror the clustering of the bulk of the matter in the Universe. In its most general form, the galaxy density can be a non-local and stochastic function of the underlying dark matter density. This galaxy "bias" - the relationship between the spatial distribution of galaxies and the underlying dark matter density field - is a result of the varied physics of galaxy formation which can cause the spatial distribution of baryons to differ from that of dark matter. Stochasticity appears to have little effect on bias except for adding extra variance (e.g., Scoccimarro 2000), and non-locality can be taken into account to first order by using smoothed densities over larger scales. In this approximation, the smoothed galaxy density contrast is a general function of the underlying dark matter density contrast on some scale:

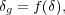(19)

where ( / ) - 1 and is the mean mass density on that scale. If we assume f() is a linear function of , then we can define the linear galaxies bias b as the ratio of the mean overdensity of galaxies to the mean overdensity of mass,

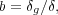(20)

and can in theory depend on scale and galaxy properties such as luminosity, morphology, color and redshift. In terms of the correlation function, the linear bias is defined as the square root of the ratio of the two-point correlation function of the galaxies relative to the dark matter:

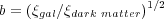(21)

and is a function of scale. Note that _{dark matter} is the Fourier transform of the dark matter power spectrum. The bias of galaxies relative to dark matter is often referred to as the absolute bias, as opposed to the relative bias between galaxy populations (discussed below).

The concept of galaxies being a biased tracer of the underlying total mass field (which is dominated by dark matter) was introduced by Kaiser (1984) in an attempt to reconcile the different clustering scale lengths of galaxies and rich clusters, which could not both be unbiased tracers of mass. Kaiser (1984) show that clusters of galaxies would naturally have a large bias as a result of being rare objects which formed at the highest density peaks of the mass distribution, above some critical threshold. This idea is further developed analytically by Bardeen et al. (1986) for galaxies, who show that for a Gaussian distribution of initial mass density fluctuations, the peaks which first collapse to form galaxies will be more clustered than the underlying mass distribution. Mo & White (1996) use extended Press-Schechter theory to determine that the bias depends on the mass of the dark matter halo as well as the epoch of galaxy formation and that a linear bias is a decent approximation well into the non-linear regime where > 1. The evolution of bias with redshift is developed in theoretical work by Fry (1996) and Tegmark & Peebles (1998), who find that the bias is naturally larger at earlier epochs of galaxy formation, as the first galaxies to form will collapse in the most overdense regions of space, which are biased (akin to mountain peaks being clustered). They further show that regardless of the initial amplitude of the bias factor, with time galaxies will become unbiased tracers of the mass distribution (b → 1 as t → ). Additionally, Mann et al. (1998) find that while bias is generally scale-dependent, the dependence is weak and on large scales the bias tends towards a constant value.

A galaxy population can be "anti-biased" if b < 1, indicating that galaxies are less clustered than the dark matter distribution. As discussed below, this appears to be the case for some galaxy samples at low redshift. The galaxy bias of a given observational sample is often inferred by comparing the observed clustering of galaxies with the clustering of dark matter measured in a cosmological simulation. Therefore the bias depends on the cosmological model used in the simulation. The dominant relevant cosmological parameter is ₈, defined as the standard deviation of galaxy count fluctuations in a sphere of radius 8 h^-1 Mpc, and the absolute bias value inferred can be simply scaled with the assumed value of ₈. As discussed in section 9.1 below, the absolute galaxy bias can also be estimated from the data directly, without having to resort to comparisons with cosmological simulations, by using the ratio of the two-point and three-point correlation functions, which have different dependencies on the bias. While this measurement can be somewhat noisy, it has the advantage of not assuming a cosmological model from which to derive the dark matter clustering. This measurement is performed by Verde et al. (2002) and Gaztañaga et al. (2005), who find that galaxies in 2dFGRS have a linear bias value very close to unity on large scales.

The relative bias between different galaxy populations can also be measured and is defined as the ratio of the clustering of one population relative to another. This is often measured using the ratio of the projected correlation functions of each population:

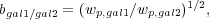(22)

where both measurements of w_p(r_p) have been integrated to the same value of _max. The relative bias is used to compare the clustering of galaxies as a function of observed parameters and does not refer to the clustering of dark matter. It is a useful way to compare the observed clustering for different galaxy populations without having to rely on an assumed value of ₈ for the dark matter.