4. REAL AND REDSHIFT SPACE CLUSTERING

Measurements of the two-point correlation function use the redshift of a galaxy, not its distance, to infer its location along the line of sight. This introduces two complications: one is that a cosmological model has to be assumed to convert measured redshifts to inferred distances, and the other is that peculiar velocities introduce redshift space distortions in parallel to the line of sight (Sargent & Turner 1977). On the first point, errors on the assumed cosmology are generally subdominant, so that while in theory one could assume different cosmological parameters and check which results are consistent with the assumed values, that is generally not necessary. On the second point, redshift space distortions can be measured to constrain cosmological parameters, and they can also be integrated over to recover the underlying real space correlation function.

On small spatial scales ( 1 h^-1 Mpc), within collapsed virialized overdensities such as groups and clusters, galaxies have large random motions relative to each other. Therefore while all of the galaxies in the group or cluster have a similar physical distance from the observer, they have somewhat different redshifts. This causes an elongation in redshift space maps along the line of sight within overdense regions, which is referred to as "Fingers of God". The result is that groups and clusters appear to be radially extended along the line of sight towards the observer. This effect can be seen clearly in Fig. 4, where the lower left panel shows galaxies in redshift space with large "Fingers of God" pointing back to the observer, while in the lower right panel the "Fingers of God" have been modeled and removed. Redshift space distortions are also seen on larger scales ( 1 h^-1 Mpc) due to streaming motions of galaxies that are infalling onto structures that are still collapsing. Adjacent galaxies will all be moving in the same direction, which leads to coherent motion and causes an apparent contraction of structure along the line of sight in redshift space (Kaiser 1987), in the opposite sense as the "Fingers of God".

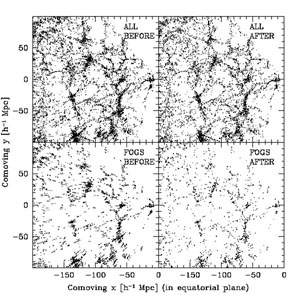Figure 4. An illustration of the "Fingers of God" (FoG), or elongation of virialized structures along the line of sight, from Tegmark et al. (2004). Shown are galaxies from a slice of the SDSS sample (projected here through the declination direction) in two dimensional comoving space. The top row shows all galaxies in this slice (67,626 galaxies in total), while the bottom row shows galaxies that have been identified as having "Fingers of God". The right column shows the position of these galaxies in this space after modeling and removing the effects of the "Fingers of God". The observer is located at (x, y = 0, 0), and the "Fingers of God" effect can be seen in the lower left panel as the positions of galaxies being radially smeared along the line of sight toward the observer.

The real-space correlation function, (r), measures the underlying physical clustering of galaxies, independent of any peculiar velocities. Therefore, in order to recover the real-space correlation function, one can measure in two dimensions, both perpendicular to and along the line of sight. Following Fisher et al. (1994), v₁ and v₂ are defined to be the redshift positions of a pair of galaxies, s to be the redshift space separation (v₁ - v₂), and l = 1/2 (v₁ + v₂) to be the mean distance to the pair. The separation between the two galaxies across (r_p) and along () the line of sight are defined as

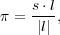(13)

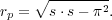(14)

One can then compute pair counts over a two-dimensional grid of separations to estimate (r_p, ). (s), the one-dimensional redshift space correlation function, is then equivalent to the azimuthal average of (r_p, ).

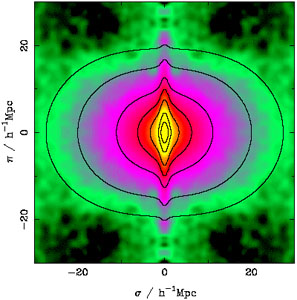Figure 5. The two-dimensional redshift space correlation function from 2dFGRS (Peacock et al. 2001). Shown is (rp, ) (in the figure is used instead of rp), the correlation function as a function of separation across ( or rp) and along () the line of sight. Contours show lines of constant at = 10, 5, 2, 1, 0.5, 0.2, 0.1. Data from the first quadrant (upper right) are reflected about both the and axes, to emphasize deviations from circular symmetry due to redshift space distortions.

An example of a measurement of (r_p, ) is shown in Fig. 5. Plotted is as a function of separation r_p (defined in this figure to be ) across and along the line of sight. What is usually shown is the upper right quadrant of this figure, which here has been reflected about both axes to emphasize the distortions. Contours of constant follow the color-coding, where yellow corresponds to large values and green to low values. On small scales across the line of sight (r_p or < ~ 2 h^-1 Mpc) the contours are clearly elongated in the direction; this reflects the "Fingers of God" from galaxies in virialized overdensities. On large scales across the line of sight (r_p or > ~ 10 h^-1 Mpc) the contours are flattened along the line of sight, due to "the Kaiser effect". This indicates that galaxies on these linear scales are coherently streaming onto structures that are still collapsing.

As this effect is due to the gravitational infall of galaxies onto massive forming structures, the strength of the signature depends on _matter. Kaiser (1987) derived that the large-scale anisotropy in the (r_p, ) plane depends on _matter / b on linear scales, where b is the bias or the ratio of density fluctuations in the galaxy population relative to that of dark matter (discussed further in the next section below). Anisotropies are quantified using the multipole moments of (r_p, ), defined as

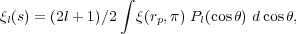(15)

where s is the distance as measured in redshift space, P_l are Legendre polynomials, and is the angle between s and the line of sight. The ratio ₂ / ₀, the quadrupole to monopole moments of the two-point correlation function, is related to in a simple manner using linear theory (Hamilton 1998):

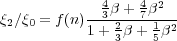(16)

where f(n) = (3 + n) / n and n is the index of the two-point correlation function in a power-law form: r^-(3+n) (Hamilton 1992).

Peacock et al. (2001) find using measurements of the quadrupole-to-monopole ratio in the 2dFGRS data (see Fig. 5) that = 0.43 ± 0.07. For a bias value of around unity (see Section 5 below), this implies a low value of _matter ~ 0.3. Similar measurements have been made with clustering measurements using data from the SDSS. Very large galaxy samples are needed to detect this coherent infall and obtain robust estimates of . At higher redshift, Guzzo et al. (2008) find = 0.70 ± 0.26 at z = 0.77 using data from the VVDS and argue that measurements of as a function of redshift can be used to trace the expansion history of the Universe. We return to the discussion of redshift space distortions on small scales below in Section 6.3.

What is often desired, however, is a measurement of the real space clustering of galaxies. To recover (r) one can then project (r_p, ) along the r_p axis. As redshift space distortions affect only the line-of-sight component of (r_p, ), integrating over the direction leads to a statistic w_p(r_p), which is independent of redshift space distortions. Following Davis & Peebles (1983),

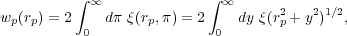(17)

where y is the real-space separation along the line of sight. If (r) is modeled as a power-law, (r) = (r / r₀)^-, then r₀ and can be readily extracted from the projected correlation function, w_p(r_p), using an analytic solution to Equation 17:

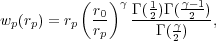(18)

where Γ is the usual gamma function. A power-law fit to w_p(r_p) will then recover r₀ and for the real-space correlation function, (r). In practice, Equation 17 is not integrated to infinite separations. Often values of _max are ~ 40-80 h^-1 Mpc, which includes most correlated pairs. It is worth noting that the values of r₀ and inferred are covariant. One must therefore be careful when comparing clustering amplitudes of different galaxy populations; simply comparing the r₀ values may be misleading if the correlation function slopes are different. It is often preferred to compare the galaxy bias instead (see next section).

As a final note on measuring the two-point correlation function, as can be seen from Fig. 3, flux-limited galaxy samples contain a higher density of galaxies at lower redshift. This is purely an observational artifact, due to the apparent magnitude limit including intrinsically lower luminosity galaxies nearby, while only tracing the higher luminosity galaxies further away. As discussed below in Section 6, because the clustering amplitude of galaxies depends on their properties, including luminosity, one would ideally only measure (r) in volume-limited samples, where galaxies of the same absolute magnitude are observed throughout the entire volume of the sample, including at the highest redshifts. Therefore often the full observed galaxy population is not used in measurements of (r), rather volume-limited sub-samples are created where all galaxies are brighter than a given absolute magnitude limit. This greatly facilitates the theoretical interpretation of clustering measurements (see Section 8) and the comparison of results from different surveys.