4. RECOGNIZING DISK-LIKE BULGES

Identifying what kind of bulge a given galaxy has is very relevant if we wish to understand the formation and evolutionary processes such galaxy went through, until it reached the physical state presented to us today. While a classical bulge, i.e. component number 2 in the list above, suggests a more violent history, including mergers, a disk-like bulge possibly indicates a quieter evolution, if it is the only bulge in the galaxy. (Although note, again, that some mergers might contribute only to material in the outer halo, and not result in the formation of a bulge.) A given galaxy can have no bulge, can have a classical bulge or a disk-like bulge, or both. It's easy to picture a bulge-less disk galaxy evolving, accreting a smaller satellite in a merger event, which would originate a classical bulge, and then developing a bar which would produce a disk-like bulge. Later, the bar can itself evolve and have its inner parts puffed up and form a box/peanut. Eventually, this galaxy not only has a classical and a disk-like bulge, but also a box/peanut. Gadotti (2009) discussed composite bulges, i.e. classical bulges with a young stellar component that could be embedded disk-like bulges, while Nowak et al. (2010) argued that NGC 3368 and NGC 3489 show a small classical bulge embedded in a disk-like bulge. Finally, Kormendy & Barentine (2010) found that NGC 4565 has a disk-like bulge inside a box/peanut.

Since disk-like bulges contribute to a smaller fraction of the total galaxy light than classical bulges (i.e. they have smaller bulge/total ratios - see e.g. Drory & Fisher 2007, Gadotti 2009), they are naturally found most often in more late-type galaxies. However, disk-like bulges can also be found in lenticular galaxies (Laurikainen et al. 2007), which can be understood in the context proposed by van den Bergh (1976, see also Kormendy & Bender 2012) of a Hubble sequence with spirals and lenticulars forming parallel branches. Durbala et al. (2008) found that galaxies hosting disk-like bulges are predominantly in low density environments (see also Zhao 2012). Mathur et al. (2011) and Orban de Xivry et al. (2011) found that the bulges of narrow line Seyfert 1 galaxies (AGN accreting at high rates and powered by less massive black holes) are disk-like bulges, an important clue to understand the fueling of AGN activity by bars (Shlosman et al. 1989) and the connected growth of bulges and their central black holes.

Note that a disk-like bulge can be any of the components number 5 through 9 in the list above, or any combination of them. Classical and disk-like bulges can therefore be distinguished by their morphology. Although this can work well (see e.g. Fisher & Drory 2010), it is to a large extent subjective, and there are more objective ways to proceed with such a separation.

Another method to distinguish bulge types is to look at their surface brightness radial profiles. In the past, these were fitted using the de Vaucouleurs (1948) function, used to fit such profiles in ellipticals. We now know that a better fit to the profiles of both ellipticals and bulges is provided by the Sérsic (1968) function, which is a generalization of the de Vaucouleurs' function (see Caon et al. 1993):

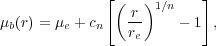(1)

where r_e is the effective radius of the bulge, i.e., the radius that contains half of its light, µ_e is the bulge effective surface brightness, i.e., the surface brightness at r_e, n is the Sérsic index, defining the shape of the profile, and c_n = 2.5(0.868n - 0.142). When n = 4, the Sérsic funtion becomes the de Vaucouleurs' function; when n = 1, it is an exponential function, and, when n = 0.5, a Gaussian. Important properties of the Sérsic function and its application to fit galaxy light profiles can be found in Trujillo et al. (2001) and Graham & Driver (2005).

There is evidence that the light profiles of most classical bulges, as well as ellipticals, are better described by a Sérsic function with n > 2, whereas most disk-like bulges have n < 2, i.e., closer to an exponential function, as disks (e.g. Fisher & Drory 2008, Gadotti 2009). Figure 11 shows schematically the light profiles of an elliptical galaxy and of disk galaxies with bulges following Sérsic functions with different values of n. For a real (and barred) galaxy, see the right panel in Fig. 4. Note that in order to obtain bulge structural parameters one needs to decompose either the galaxy light profile (1D decomposition) or better the whole galaxy image (2D decomposition) into the main different galactic components.

Figure 11. Top left: a Sérsic function with n = 4, that could represent the light profile of an elliptical galaxy. Top right: a Sérsic function with n = 3 - that could represent the bulge in a galaxy of early Hubble type - plus an exponential function, representing the disk of such galaxy. Bottom left: same as the latter but with a Sérsic with n = 2; and finally, bottom right: same as the latter but with n = 1. The sum of both components is shown when this applies. Also indicated are the difference between the bulge effective and central surface brightness, µe - µ0 (note that this does not consider effects from a PSF), and the positions of re and the disk scale length h, for each model.

However, the threshold at n = 2 to separate classical and disk-like bulges is set arbitrarily, and still lacks a clear physical justification. Furthermore, the uncertainty on the measure of n - typically 0.5 - is large compared to the range of values n typically assumes in bulges: 0.5 < n < 6 (see Gadotti 2008, Gadotti 2009). This means that using the Sérsic index to discriminate between bulge types is prone to misclassifications.

A more physically motivated criterion to separate classical and disk-like bulges can be devised using the Kormendy (1977) relation between <µ_e> (the mean surface brightness within r_e) and r_e (Carollo 1999). The fact that classical bulges and elliptical galaxies seem to follow this relation suggests a similarity on the physics behind their formation. If the formation of disk-like bulges considerably involves different physical processes then they do not necessarily follow this relation. Figure 12 shows the Kormendy relation for elliptical galaxies and bulges, the latter separated by Sérsic index at n = 2. It is clear that, in contrast to most bulges with n > 2, many of those with n < 2 occupy a different locus in the <µ_e> - r_e plane. This tells us two things: (i): there seem to be bulges with different properties, and (ii): the Sérsic index is a first-order approximation to distinguish these bulges. However, one also sees that many bulges with n<2 follow the same relation set by ellipticals, and several bulges with n > 2 do not. A follow-up in this analysis is then to define classical bulges as those which follow the Kormendy relation of ellipticals within 3 boundaries. Conversely, disk-like bulges are then those which do not fall within these boundaries. It is important to note that this criterion is independent of the Sérsic index. This is done in Gadotti (2009) and it is found that disk-like bulges satisfy the following relation:

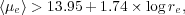(2)

where measurements are made using the SDSS i-band, and r_e is in units of a parsec.

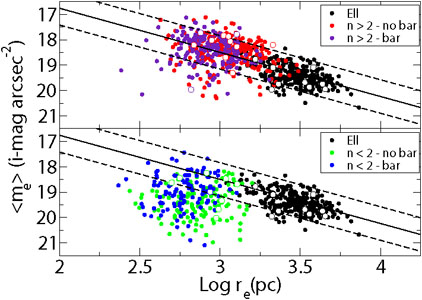Figure 12. Kormendy (1977) relation for elliptical galaxies and bulges. The latter separated by Sérsic index: those with n > 2 appear only in the top panel, and those with n < 2 appear only at the bottom panel. The solid line is a fit to the elliptical galaxies, while the dashed lines mark the corresponding 3 boundaries. A more physically motivated definition for disk-like bulges is devised using the lower 3 boundary: disk-like bulges fall below this boundary and are thus outliers in the Kormendy relation set by ellipticals. [Taken from Gadotti 2009.]

Figure 13 shows a density plot of the < µ_e > - r_e plane using the same data as in Fig. 12, but without making any separation between galaxy/bulge types. It shows that the loci occupied by elliptical galaxies, classical bulges and disk-like bulges correspond to three well-defined `islands' of points. A 2D Kolmogorov-Smirnov test shows that these groups of points are indeed different populations, with a statistical confidence level of 5 . This is important because it shows that the definition of disc-like bulges from Eq. 2 is not an artificial one, but in fact statistically justified. There is a statistically significant gap between classical and disk-like bulges in the <µ_e> - r_e plane. Since the sample used is drawn from a volume-limited sample, and has well-known selection effects, one can show that this gap cannot be attributable to spurious effects from the selection of the sample (see Gadotti 2009).

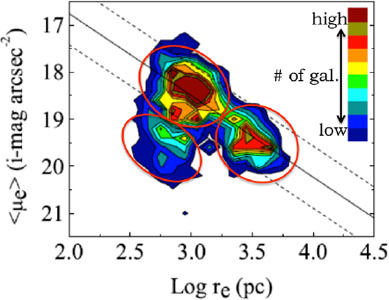Figure 13. Same as Fig. 12, but with no separation on galaxy/bulge type, and plotted as iso-density contours. Elliptical galaxies, classical bulges and disk-like bulges correspond to well defined `islands'. It can be shown that these islands represent populations of distinct physical systems with a confidence level of 5 . This shows that the separation between classical and disk-like bulges using Eq. 2 is not artificial, and rather has solid physical grounds. [Adapted from Gadotti 2009.