5. SCALING RELATIONS

Bulges and elliptical galaxies follow a number of relations among their structural parameters which provide fundamental clues to their formation and evolutionary histories. Starting from first principles, from the Virial Theorem, we have:

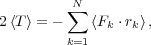(3)

where, for a system with N particles, F_k is the force acting on particle k, located at r_k. This theorem basically states that twice the kinetic energy averaged over time in the system (the left-hand side of Eq. 3) equals its potential energy averaged over time (the right-hand side). For any bound system of particles interacting by means of an inverse square force, and with a number of non-trivial assumptions, we can derive (see e.g. Zaritsky et al. 2006):

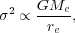(4)

or:

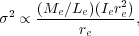(5)

leading to:

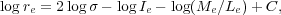(6)

where M_e / L_e is the mass/light ratio within r_e, I_e is the mean surface brightness within r_e, and C is a constant.

Equation 6 is the famous Fundamental Plane (hereafter FP, Djorgovski & Davis 1987, Dressler et al. 1987), and one expects that at least ellipticals - for which the violations of the assumptions are less evident - should follow it. If the mass/light ratio is constant, say among massive ellipticals and classical bulges, one thus expect to see a relation such as r_e ² I_e^-1, which is, however, not borne out by recent observations. For instance, Bernardi et al. (2003) found r_e ^1.49 I_e^-0.75 using SDSS r-band data for over 8000 galaxies. This difference between the observed and expected values of the coefficients is called the tilt of the FP. It results, partly, from the fact that we are neglecting any variation in the mass/light ratio, which can be caused not only by variations in the stellar population content (i.e. stellar age and chemical properties), but also in the dark matter content. In fact, Boylan-Kolchin et al. (2005) found in merger simulations that the dark matter fraction within r_e varies with galaxy mass. Nevertheless, Trujillo et al. (2004) argued that the most important factor is the violation of the assumption that all systems are homologous. If systems are not homologous, this means that the shape of the gravitational potential might depend on scale, i.e. on the size of the system. This is consistent with the finding that the Sérsic index varies with system luminosity (see e.g. Desroches et al. 2007, Graham & Worley 2008, Gadotti 2009, Laurikainen et al. 2010).

The FP can also be expressed in a space with axes directly related to important physical parameters, such as mass and mass/light ratio. Bender et al. (1992) did just that, and defined the -space, where ₁, ₂ and ₃ are three orthogonal axes, defined as functions of r_e, and I_e, in such a way that ₁ is proportional to the logarithm of the dynamical mass, ₂ is proportional mainly to the logarithm of I_e, and ₃ is proportional to the logarithm of the mass/light ratio. We will see shortly below where bulges and elliptical galaxies are in the -space.

Projections of the FP are also very important tools to understand the formation histories of bulges and ellipticals. One such projection is the Faber & Jackson (1976) relation:

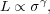(7)

where L is the galaxy total luminosity. The canonical value of that can be derived on theoretical grounds is = 4, which is about what Faber & Jackson (1976) found. More recent work on this subject (see e.g. Gallazzi et al. 2006, Lauer et al. 2007, Desroches et al. 2007) shows that the slope of the Faber & Jackson (1976) relation varies from 2 for low mass galaxies to 8 for the most massive ellipticals. It thus seems that the relation is curved. The fact that less massive ellipticals show a flatter relation suggests that processes involving large amounts of energy dissipation are more important in the formation of these systems, as opposed to more massive ellipticals (see Boylan-Kolchin et al. 2006).

Another useful projection of the FP is the luminosity-size relation. In principle, it should not be a surprise that the more massive a system is the larger it is too. However, different systems might follow different luminosity-size relations, indicating that the ways they grow - their formation histories - are different. Desroches et al. (2007) and Hyde & Bernardi (2009), among others, found that the luminosity-size relation is curved, a result that is at odds with the finding of e.g. Nair et al. (2010). A crucial point in studies on fundamental relations is sample selection. To obtain a clean sample including e.g. only elliptical galaxies is not as simple as it sounds. In addition, if a given sample includes both ellipticals and e.g. disk galaxies with massive bulges, it is not straightforward to compare sizes and luminosities between ellipticals and disk galaxies if one does not perform a proper bulge/disk decomposition to exclude the disk in the measurements corresponding to disk galaxies. Studies such as Bernardi et al. (2003) and Hyde & Bernardi (2009) make selection cuts in parameter spaces including concentration, spectral properties, properties of light profile fits with a single component, and axial ratio, which in principle should yield mostly elliptical galaxies as output. Although objective, these criteria are however likely to include many disk galaxies (see e.g. discussion in Gadotti 2009, Sect. 4.4). The sample in Nair et al. (2010) has visual classification, which can be argued to be more accurate to separate disk galaxies from ellipticals, even if to some extent subjective, and their different conclusions possibly stem partly from this difference in sample selection. The curvature in the luminosity-size relation can simply be a result of putting together measurements that correspond to systems with different natures. The case of a different luminosity-size relation for brightest cluster galaxies is well-known (e.g. Bernardi 2009).

What do these fundamental scaling relations tell us? The fact that we see galaxies following relations derived from simple theoretical considerations, which essentially include only the action of gravity, is a demonstration that gravity indeed plays a major role here. But as we saw above, it is the deviations of the expected relations that have a lot to teach us, revealing other facets in the history of galaxies, such as dark matter content and other aspects of baryonic physics. Reasons for these deviations include dissipation of energy via dynamical friction and gas viscosity, and feedback mechanisms from either supernovae or active galactic nuclei. Let us now go back to the issue of the different families of bulges and see how the loci these bulges occupy in the fundamental relations discussed above compare with the corresponding locus of ellipticals.

Figure 14 shows the -space formulation of the FP from Pierini et al. (2002) in the top panels, and Gadotti (2009) in the bottom panels. Pierini et al. (2002) did not perform structural decompositions, and thus their measures correspond to galaxies as whole systems. However, the top left panel shows their results for elliptical and lenticular galaxies, presumably then a good approximation for the results concerning elliptical galaxies only. In addition, the top right panel shows their results for very late-type disk galaxies, presumably bulge-less disks, and thus a good approximation for the results concerning just disks. The results shown in the bottom panels correspond to ellipticals, and classical and disk-like bulges, obtained through bulge/bar/disk decompositions, and thus correspond truly to bulges alone, in the case of disk galaxies. In the edge-on view of the -space, classical bulges deviate slightly from ellipticals, and disk-like bulges deviate markedly. In the face-on projection, ellipticals, classical and disk-like bulges occupy three different loci. Comparing the top and bottom panels one sees that in both projections disk-like bulges occupy loci similar to those occupied by disks. This lends strong support to, firstly, the physical reality of different bulge families, and, secondly, the connected formation histories of disk-like bulges and disks.

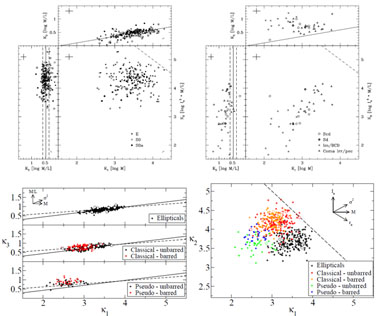Figure 14. Near-infrared Fundamental Plane in -space for elliptical and lenticular galaxies (top left) and very late-type disk galaxies (top right). These results concern galaxies as whole, i.e. with no structural decomposition. The bottom panels show the SDSS i-band Fundamental Plane in -space for elliptical galaxies, classical and disk-like bulges, obtained via bulge/bar/disk decompositions. In both projections of the Fundamental Plane, disk-like bulges lie on the locus occupied by (presumably) pure disks. [Adapted from Pierini et al. 2002 and Gadotti 2009].

Figure 15 is the 4 offset of the relation of ellipticals with respect to that of classical bulges. It demonstrates decidedly that (i), classical bulges and elliptical galaxies have different formation histories, and (ii), at the high mass end, at least, classical bulges are not just scaled down ellipticals surrounded by disks. If you put a disk around a massive elliptical you end up with a galaxy unlike real disk galaxies. Similar results were also found by Laurikainen et al. (2010). The mass- relation, again arguably a better equivalent of the Faber & Jackson (1976) relation, has also been shown to be different for ellipticals and classical bulges (Gadotti & Kauffmann 2009). Gadotti & Sánchez-Janssen (2012) discussed the intriguing nature of the spheroid in the Sombrero galaxy, and, using several scaling relations, found that it resembles more an elliptical than a classical bulge.

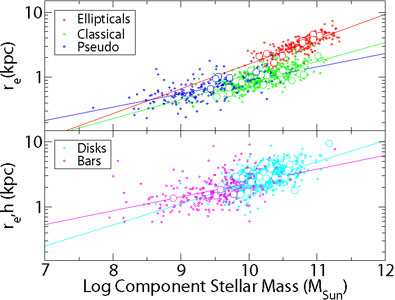Figure 15. Mass-size relations of ellipticals, classical and disk-like bulges, bars and disks. The offset of the relation of ellipticals with respect to that of classical bulges has a statistical significance of 4, indicating that the formation histories of these systems is different. This also shows that, at least at the high mass end, classical bulges are definitely not just scaled down ellipticals surrounded by disks. [Taken from Gadotti 2009].