2. PHENOMENOLOGY

2.1. The luminosity function

Theory provides the mass function of dark halos. Observation yields the luminosity function of galaxies, usually fit by a Schechter (1976) function. Comparison of the two is at first sight disconcerting. One can calculate the M/L ratio for the two functions to overlap at one point, for a mass M^∗ corresponding to L_∗. Define t_cool = 3 / 2nkT / [n² (T)] and t_dyn = 3 / (32 G )^1/2. For star formation to occur, cooling is essential, and the condition t_cool < t_dyn guarantees cooling in an inhomogeneous galactic halo where gas clouds collide at the virial velocity. One finds that

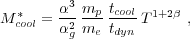where = e² / ( c) and _g = G m_p² / e² are the electromagnetic and gravitational fine structure constants. For a cooling function (T) T, over the relevant temperature range (10⁵-10⁷ K), one can take -1/2 for a low metallicity plasma (Gnat & Sternberg 2007). The result is that one finds a characteristic galactic halo mass, in terms of fundamental constants, to be of order 10¹² M (Silk 1977). The inferred value of the mass-to-light ratio M / L is similar to that observed for L_∗ galaxies. This is a success for theory: dissipation provides a key ingredient in understanding the stellar masses of galaxies, at least for the "typical" galaxy. The characteristic galactic mass is understood by the requirement that cooling within a dynamical time is a necessary condition for efficient star formation (Fig. 1).

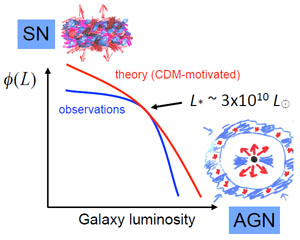Figure 1. Role of feedback in modifying the galaxy luminosity function

2.2. Star formation rate and efficiency

In addressing star-forming galaxies, the problem reduces to our fundamental ignorance of star formation. Phenomenology is used to address this gap in our knowledge. Massive star feedback in giant molecular clouds, the seat of most galactic star formation, implies a star formation efficiency (SFE), defined as star formation rate (SFR) divided by the ratio of gas mass to dynamical or disk rotation time, of around 2%. This is also found to be true globally in the Milky Way (MW) disk.

Remarkably, a similar SFE is found in nearby star-forming disk galaxies. Indeed, SFRs per unit area in disk galaxies, both near and far, can be described by a simple law, with SFE being the controlling parameter (Silk 1997, Elmegreen 1997):

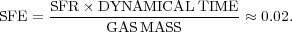(1)

The motivation comes from the gravitational instability of cold gas-rich disks, which provides the scaling, although the normalization depends on feedback physics. For the global law, in terms of SFR and gas mass per unit area, SN regulation provides the observed efficiency of about 2% which fits essentially all local star-forming galaxies. One finds from simple momentum conservation that SFE = _gas v_cool m*_SN / E_SN^initial 0.02. Here, v_cool is the SN-driven swept-up shell velocity at which approximate momentum conservation sets in and m*_SN 150 M is the mass formed in stars per SNII, in this case for a Chabrier (2003) initial mass function (IMF). This is a crude estimator of the efficiency of SN momentum input into the interstellar medium, but it reproduces the observed global normalization of the star formation law.

The fit applies not only globally but to star formation complexes in individual galaxies such as M51 and also to starburst galaxies. The star formation law is known as the Schmidt-Kennicutt law (Kennicutt et al. 2007), and its application reveals that molecular gas is the controlling gas ingredient. In the outer parts of galaxies, where the molecular fraction is reduced due to the ambient UV radiation field and lower surface density, the SFR per unit gas mass also declines (Bigiel et al. 2011).

For disk instabilities to result in cloud formation, followed by cloud agglomeration and consequent star formation, one also needs to maintain a cold disk by accretion of cold gas. There is ample evidence of a supply of cold gas, for example in the M33 group. Other spiral galaxies show extensive reservoirs of HI in their outer regions, for example NGC 6946 (Boomsma et al. 2008) and UGC 2082 (Heald et al. 2011). Recent data extends the Schmidt-Kennicutt law to z ~ 2, with a tendency for ultraluminous starbursts at z ~ 2 to have somewhat higher SFE (Genzel et al. 2010, see Fig. 2).

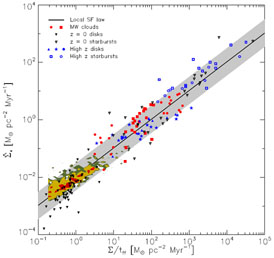Figure 2. Schmidt-Kennicutt laws on nearby (including Local Group galaxies as shaded regions) and distant galaxies, as well as Milky Way Giant Molecular Clouds (Krumholz et al. 2012). The solid line is similar to equation (1).

A more refined theoretical model needs to take account of star formation in a multi-phase interstellar medium. One expects self-regulation to play a role. If the porosity in the form of SN remnant-driven bubbles is low, there is no venting and the pressure is enhanced, clouds are squeezed, and SN explosions are triggered by massive star formation. This is followed by high porosity and blow-out, and the turbulent pressure drops. Eventually halo infall replenishes the cold gas, the porosity is lowered and the cycle recommences. Some of this complexity can be seen in numerical simulations (Agertz et al. 2011). SNe provide recirculation and venting of gas into fountains, thereby reducing the SFE and prolonging the duration of star formation in normal disk galaxies.

In fact, galaxy colors illustrate the bimodality of SFRs. Elliptical and lenticular galaxies are red, spirals are blue. This lyric does not hide a continuity in galaxy properties: most galaxies lie in either the Red Sequence or the Blue Cloud (see Fig. 3). This suggests that star formation in galaxies is either ongoing or was quenched several Gyr ago. The small fraction of intermediate population, Green Valley galaxies suggests that some galaxies have experienced a recent quenching of their star formation.

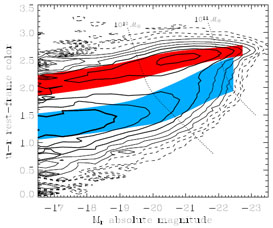Figure 3. Illustration of galaxy bimodality. The contours are the density of SDSS galaxies in color-luminosity space, after correction for selection effects (Baldry et al. 2004).

Seyfert galaxies have intermediate age stellar populations (Schawinski et al. 2007, see fig. 4) and mostly lie in the Green Valley (Schawinski 2012). This suggests that star formation is quenched by nuclear activity.

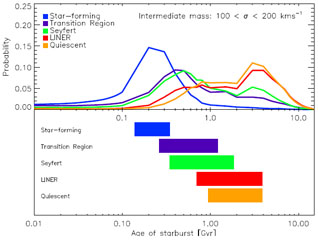Figure 4. Ages of galaxies of different activity (Schawinski et al. 2007).

2.3. Scaling relations

The global properties of early-type galaxies are known to correlate: early work focussed on L ~ _v⁴ (Faber & Jackson 1976). The early work found a slope of 4 because of the inclusion of bright and faint galaxies. The modern work finds a slope of 5 for luminous galaxies (M_B -20.5, core-Sérsic galaxies) and a slope of 2 for the less luminous spheroids, and has been distilled into the Fundamental Plane linking mass, mass-to-light ratio, and mean surface brightness at the effective radius (Bender et al. 1992).

Figure 5 shows a more modern version of the properties of early-type galaxies, to which are added globular clusters and clusters of galaxies. It is not yet understood what makes the continuity of the global properties of massive systems fragment into two branches with ultra-compact dwarfs and globular clusters on one side and dwarf spheroidals on the other.

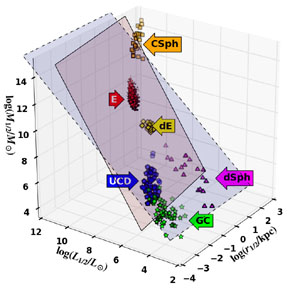Figure 5. 3D view of scaling relations of spheroidal systems from globular clusters (GC) to clusters of galaxies (CSph), via ultra-compact dwarfs (UCD), dwarf spheroidals (dSph), dwarf ellipticals (dE) and giant ellipticals (E), where the axes are half-luminosity, half-luminosity radius and total mass within half-luminosity radius (Tollerud et al. 2011). The red and blue planes respectively represent the Fundamental Plane and the "virial plane" of constant M / L.

2.4. Evolution of low mass galaxies

The accepted solution for gas disruption and dispersal in intermediate mass and massive dwarfs (halo mass ~ 10⁸ - 10¹⁰ M) is by SN feedback. SNe expel the remaining baryons in systems of halo mass up to ~ 10⁸ M, leaving behind dim remnants of dwarf galaxies (Dekel & Silk 1986). Presumably the luminous dwarfs accrete gas at later epochs. Most gas is ejected by the first generations of SNe for systems with escape velocity 50 km/s, leaving dim stellar remnants behind.

In very low-mass halos gas cannot even fall in, because its specific entropy is too high (Rees 1986). This entropy barrier amounts to a temperature barrier since the gas density, which to first order is proportional to the total mass density, is the same in different halos at a given epoch. Only halos of mass 10⁵ M trap baryons that are able to undergo early H₂ cooling and eventually form stars. Hydrodynamical simulations indicate that this lower limit is sharp (Gnedin 2000, Okamoto et al. 2008). Reionization reinforces this limit by heating the intergalactic gas to high entropy, hence suppressing subsequent star formation (see Fig. 6). The abrupt increase of the sound speed to ~ 10-20 km/s at z ~ 10 means that dwarfs of halo mass ~ 10⁶ - 10⁷ M, which have not yet collapsed and fragmented into stars, will be disrupted. However massive dwarfs are unaffected, as are the high peaks that develop into early collapsing, but rare, low mass dwarfs.

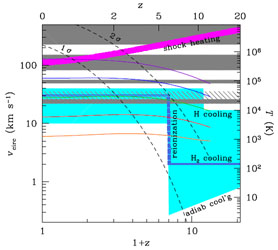Figure 6. Evolution of circular velocities (at virial radius) for halos with efficient star formation (Mamon et al. 2012). The smooth curves indicate the mean evolution of halos (with final masses log hM = 8 to 12 going upwards). The blue broken line is a model for the evolution of the minimum mass for galaxy formation (set by entropy feedback and related to the temperature of the IGM) and the cyan shaded region represents our ignorance of this parameter. The magenta curve is the maximum circular velocity for efficient gas infall. The grey shaded bands represent regions of thermal instability. The dashed curves shows 1 and 2 fluctuations from the CDM primordial density fluctuation spectrum.

2.5. Specific SFR

Other serious, not unrelated, problems arise with low mass galaxies. In the hierarchical approach, these generically form early. Theoretical models, both SAMs and hydrodynamical, appear to fail to account for the observed specific star formation rates (SFR per unit stellar mass or SSFR, Weinmann et al. 2012), producing too little star formation at late times. Metallicity-dependent star formation alleviates the high redshift problem, reducing the stellar mass that is in place early and enhancing the SSFR as needed (Krumholz & Dekel 2012). However, it leads to inconsistency at low redshift, because the change in metallicity and the gas fraction anti-correlate, hence leading to too little evolution in the SSFR.

As shown in Fig. 7, the star formation time-scale (or 1/SSFR) goes from the MW value of ~ 10 Gyr at low redshift to ~ 0.5 Gyr at z 2. This result suggests two distinct feedback-regulated modes of star formation: at low redshift via SNe and without AGN, and at high redshift with, most plausibly, quenching and possibly triggering by AGN playing a central role. One would expect a transition between these two modes as the AGN duty cycle becomes shorter beyond z ~ 1.

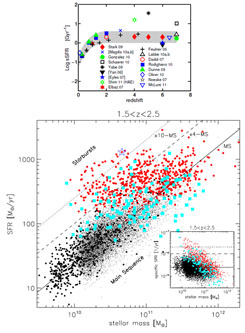Figure 7. Evolution of the specific SFR (SSFR) of galaxies of stellar mass 0.2-1 × 1010 M (Weinmann et al. 2011, top); SFR for galaxies from different samples (different color symbols), highlighting the "Main Sequence" and a population of starbursts, with SSFR mass-dependence inset (Rodighiero et al. 2011, bottom).

A related triggering mechanism appeals to enhanced rate of merging at high z (Khochfar & Silk 2011). Alternatively, it has been argued that intensified halo cold gas accretion at early epochs may account for all but the most the extreme SFRs at high z, although this may require an implausibly high SFE (Dekel et al. 2009).

2.6. Spheroidal galaxies

The baryon fraction is far from its primordial value in all systems other than massive galaxy clusters. SNe cannot eject significant amounts of gas from massive galaxies. Baryons continue to be accreted over a Hubble time and the stellar mass grows. One consequence is that massive galaxies are overproduced in the models, and that the massive galaxies are also too blue.

Galaxies like the MW have peanut-shaped pseudobulges, in contrast with the classical bulges of more massive spirals. If formed by secular gas-rich disk instabilities, they should have an age distribution similar to that of the old disk. However the formation time would be at least ~ 1 Gyr. The elevated / [Fe] ratio of our bulge favors a shorter formation time. This would be more consistent with an early disk instability phase reminiscent of that associated with clumpy gas-rich galaxies observed at z ~ 2. Massive clump merging provides a possible solution for forming bulges at a relatively late epoch (Ceverino et al. 2010).

However the time-scale (several Gyr) is too long to result in the enhanced / [Fe] ratios characteristic of massive spheroids, or even the less extreme enhancement in the MW bulge. The shorter time-scales required arise in more plausible cosmological initial conditions that result in a redshift z > 2 for pseudobulge formation (Okamoto 2012).

2.7. The role of AGN

SNe have little impact on the formation of massive galaxies. Feedback from SN explosions fails to stop the streaming of cold flows towards the centre (Powell et al. 2011). The SN ejecta tends to be driven out with only modest interaction with, and entrainment of, cold infalling gas. A more coherent and effective interaction is provided by AGN feedback from supermassive black holes (SMBH).

A clue towards a solution for these dilemmas comes from the accepted explanation of the Magorrian et al. (1998) relation, which relates SMBH mass to spheroid mass (Magorrian et al. 1998) and velocity dispersion (Ferrarese & Merritt 2000, see Fig. 8).

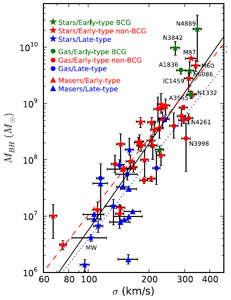Figure 8. Black hole mass versus spheroid velocity dispersion (luminosity-weighted within one effective radius), from McConnell et al. (2011)

This requires collusion between black hole growth and the initial gas content of the galaxy when the old stellar spheroid formed. One conventionally appeals to outflows from the central black hole that deliver momentum to the protogalactic gas. When the black hole is sufficiently massive, the Eddington luminosity is high enough that residual gas is ejected. An estimate of the available momentum supply come from equating the Eddington momentum with self-gravity on circumgalactic gas shells, L_Edd / c = 4 G M / = GM M_gas / r², where us the opacity. Blowout occurs and star formation terminates when the SMBH-_v relation saturates. This occurs for M_{BH v}⁴, close to the observed slope of 5 (Graham et al. 2011), and gives the correct normalization of the relation, at least in order of magnitude. This is the early feedback quasar mode.

There is also a role for AGN feedback at late epochs, when the AGN radio mode drives jets and cocoons that heat halo gas, inhibit cooling, resolve the galaxy luminosity function bright end problem and account for the red colors of massive early-type galaxies. AGN feedback in the radio mode may also account for the suppression in numbers of intermediate mass and satellite galaxies (e.g., Cattaneo et al. 2009 and references therein). Feedback from AGN in the host galaxies also preheats the halo gas that otherwise would be captured by satellites.

2.8. Galaxies downsize

Our understanding of galaxy formation is driven by observations. Prior to 2000 or so, it was accepted that hierarchical galaxy formation predicted that small galaxies form prior to massive galaxies. The first indications that this was in error came from the recognition that more massive early-type galaxies have redder colors (de Vaucouleurs 1961), higher metallicities (Faber 1973) and enhanced [] / [Fe] metallicity ratios (Ziegler et al. 2005), indicative of an older stellar population with a shorter star formation time (see Fig. 9).

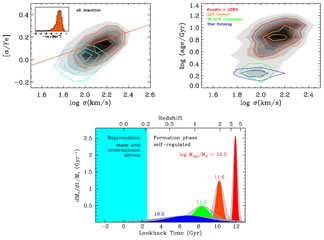Figure 9. Metallicity ratio and age versus galaxy velocity dispersion (i.e. mass) and history of star formation (Thomas et al. 2010)

This effect is called downsizing, as the most massive galaxies have their stellar populations in place early. In effect, we have a cosmic clock: incorporation into stars of debris from SNe II ( 10⁸ yr) versus SNe I ( 10⁹ yr) provides a means of dating the duration of star formation. This result was soon followed by infrared observations that showed that stellar mass assembly favored more massive systems at earlier epochs (González et al. 2011a).

2.9. Morphological evolution

We cannot do justice in this review to a largely phenomnological discussion of morphological evolution of both disk and irregular galaxies. Here, observations are far ahead of theory. However, there are strong arguments to support a continuous sequence between dwarf spheroidal galaxies and S0 galaxies (Kormendy & Bender 2012). The transformation applies to the disk components and may involve ram pressure stripping of cold gas (Gunn & Gott 1972) as well as galaxy harrassment (Moore et al. 1998). This sequence seems to acts in parallel to the pseudobulges or bulges of S0 galaxies being generated via stripped/harassed or simply starved disk galaxies (Kormendy & Bender 2012).