Copyright © 2005 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 2005. 43:
727-768 Copyright © 2005 by Annual Reviews. All rights reserved |
In the near future, when a proper census of ULIRGs up to z
3
will have been carried out, the fraction of the CIB at ~ 1 mm not
accounted for should give an indication of the contribution from sources
at larger redshifts. Deep surveys at ~ 1-2 mm are the only obvious tool
to find most of these sources. However, the limiting factor of the
surveys is not only detector sensitivity or photon noise but also
confusion. We concentrate in this section only on extragalactic sources
confusion. Source confusion in the far-infrared is illustrated in
Figure 11.
 |
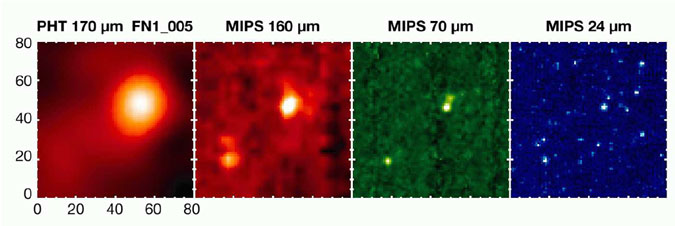Figure 11. Effects of confusion in the far-infrared. Observation of a source in the ELAIS-N1/FIRBACK field in a 400 × 400 square arcsec box. All images have been resampled to 5 arcsec per pixel, which oversamples the far-infrared maps but undersamples the mid-infrared map. From left to right: 373 mJy ISOPHOT 170 µm source with about 128s of integration (FIRBACK survey, Dole et al. 2001); labels indicate the 5 arcsec pixels; Spitzer/MIPS 160 µm with about 16s of integration (SWIRE survey, Lonsdale et al. 2004); MIPS 70 µm with about 80s of integration (SWIRE); MIPS 24 µm with about 160s of integration (SWIRE). Notice (1) the ISO 170 µm source is marginally resolved with MIPS 160, and is unambiguously resolved at 70 µm and 24 µm; (2) the two fainter MIPS 160 µm resolved sources (bottom left) create fluctuations in the ISO 170 µm map that produce the confusion noise when the resolution is limited. |
Predicting or measuring confusion depends on the scientific goal of
the measurement
(Helou & Beichman
1990;
Dole et al. 2003;
Lagache et al. 2003).
Performing an unbiased far-infrared or submillimeter survey
and getting a complete sample has different requirements than
following-up in the far-infrared an already known near-infrared source
to get an SED and/or a photometric redshift. In the former case, one
has to tightly control the statistical properties of the whole sample;
in the latter case, completeness is irrelevant, and even a low
photometric accuracy is adequate. We thus favor the use of a term like
"unbiased confusion" for the former case. New techniques are being
developed to use a priori information at shorter wavelength (e.g.,
8 µm with Spitzer/IRAC and 24 µm with
MIPS) to infer some statistical properties (such as source density or
SED) of sources at longer wavelength (e.g., 24 or 160 µm,
respectively), and thus to beat unbiased confusion. Predicting unbiased
confusion (for instance
Condon 1974;
Franceschini et
al. 1989;
Helou & Beichman
1990;
Dole et al. 2003;
Lagache et al. 2003;
Takeuchi et al. 2004;
Negrello et al. 2004)
requires the knowledge of at least the
number-count distribution of the galaxies. In practice, models
(validated at some point by observations) are used. Because the shape
of the counts in a log(N) -
log(S
)
diagram varies with the flux density
S, the
fluctuation level of faint sources below
S
also vary. This fluctuation level gives an
estimate of the unbiased confusion using a photometric criterion
(Lagache & Puget
2000;
Dole et al. 2003;
Lagache et al. 2003).
At very faint fluxes,
when the background is almost resolved, the photometric criterion will
obviously give a very small value for the unbiased confusion level,
but the observations will be limited by the confusion due to the high
density of faint resolved sources. Thus, another criterion, the source
density criterion for unbiased confusion (SDC,
Dole et al. 2003;
Dole et al. 2004b),
needs to be computed and compared to the photometric criterion.
In the infrared and submillimeter range below 300 µm, the unbiased confusion is in general better predicted by the source density criterion for current and future facilities, because the angular resolution has improved (e.g. from ISO to Spitzer). At longer wavelengths, the photometric criterion is more useful. We use the model of Lagache et al. (2004) to predict unbiased confusion. Fifteen-meter submillimeter telescopes are limited by the confusion at 1.2 mJy at 850 µm and at 0.5 mJy at 1.2 mm. Ongoing surveys (Smail et al. 2002; Greve et al. 2004) already reach or are about to reach these levels. If we want to resolve about 80% of the CIB, which corresponds to 56 µJy at 850 µm and 20 µJy at 1.3 mm, one would need a ~ 90-m telescope at 850 µm and a ~ 150-m telescope at 1.4 mm. Future facilities for infrared and submillimeter observations include far-infrared space observatories such as Herschel, SPICA, and SAFIR, survey missions like ASTRO-F and Planck, a larger near-infrared and mid-infrared observatory, JWST, and a ground-based submillimeter interferometer, ALMA. In order to detect LIRGs at z ~ 3, experiments operating at 15, 24, 70, 160, 450, 850, 1380 µm respectively should reach a sensitivity of 1, 1, 8, 50, 200, 70, 30 µJy, respectively (see Figure 12). The spectral window around 450 µm seems the most effective to reach these galaxies. This constraint is somewhat relaxed if one wants to detect ULIRGs at z ~ 3, in which case the required sensitivities are multiplied by about 10.
 |
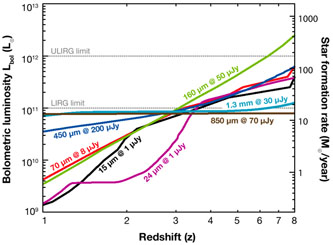Figure 12. Sensitivity to the bolometric
luminosity (and star-formation
rate, assuming star-forming galaxies) of hypothetical surveys
designed to detect LIRGs at z ~ 3. The required sensitivities are:
at 15 µm:
S |
In the near future, ASTRO-F, Herschel/SPIRE and Planck
will be mostly limited by confusion. At long wavelengths, to
probe most of the CIB source population and to detect enough early
mergers made by building blocks not yet affected by star formation and
evolution, large extragalactic surveys will have to be conducted with
ALMA. These surveys will take a substantial fraction of the time
(Lagache et al. 2003).
As an example, mapping one square degree at
1.3 mm at the 5
sensitivity of 1 mJy - ~ 50% of the CIB
is resolved - takes 138 days without including overheads.