This section discusses some ways in which the standard model could be extended. At present, there is no positive evidence in favor of any of these possibilities, which are becoming increasingly constrained by the data, though there always remains the possibility of trace effects at a level below present observational capability.
2.1. More general perturbations
The standard cosmology assumes adiabatic, Gaussian perturbations. Adiabaticity means that all types of material in the Universe share a common perturbation, so that if the space-time is foliated by constant-density hypersurfaces, then all fluids and fields are homogeneous on those slices, with the perturbations completely described by the variation of the spatial curvature of the slices. Gaussianity means that the initial perturbations obey Gaussian statistics, with the amplitudes of waves of different wavenumbers being randomly drawn from a Gaussian distribution of width given by the power spectrum. Note that gravitational instability generates non-Gaussianity; in this context, Gaussianity refers to a property of the initial perturbations, before they evolve.
The simplest inflation models, based on one dynamical field, predict adiabatic perturbations and a level of non-Gaussianity which is too small to be detected by any experiment so far conceived. For present data, the primordial spectra are usually assumed to be power laws.
For typical inflation models, it is an approximation to take the
spectra as power laws, albeit usually a good one. As data quality
improves, one might expect this approximation to come under pressure,
requiring a more accurate description of the initial spectra,
particularly for the density perturbations. In general, one can expand
ln
2 as
 |
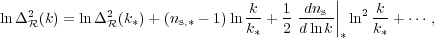(9) |
where the coefficients are all evaluated at some scale k*. The term dns / dlnk|* is often called the running of the spectral index [13]. Once non-power-law spectra are allowed, it is necessary to specify the scale k* at which the spectral index is defined.
2.1.2. Isocurvature perturbations
An isocurvature perturbation is one which leaves the total density unperturbed, while perturbing the relative amounts of different materials. If the Universe contains N fluids, there is one growing adiabatic mode and N-1 growing isocurvature modes (for reviews see Ref. 12 and Ref. 7). These can be excited, for example, in inflationary models where there are two or more fields which acquire dynamically-important perturbations. If one field decays to form normal matter, while the second survives to become the dark matter, this will generate a cold dark matter isocurvature perturbation.
In general, there are also correlations between the different modes, and so the full set of perturbations is described by a matrix giving the spectra and their correlations. Constraining such a general construct is challenging, though constraints on individual modes are beginning to become meaningful, with no evidence that any other than the adiabatic mode must be non-zero.
An alternative to laying down perturbations at very early epochs is that they are seeded throughout cosmic history, for instance by topological defects such as cosmic strings. It has long been excluded that these are the sole original of structure, but they could contribute part of the perturbation signal, current limits being just a few percent [15]. In particular, cosmic defects formed in a phase transition ending inflation is a plausible scenario for such a contribution.
Multi-field inflation models can also generate primordial non-Gaussianity (reviewed, e.g., in Ref. 7). The extra fields can either be in the same sector of the underlying theory as the inflaton, or completely separate, an interesting example of the latter being the curvaton model [16]. Current upper limits on non-Gaussianity are becoming stringent, but there remains strong motivation to push down those limits and perhaps reveal trace non-Gaussianity in the data. If non-Gaussianity is observed, its nature may favor an inflationary origin, or a different one such as topological defects.
Dark matter properties are discussed in the article by Drees and
Gerbier in this volume. The simplest assumption concerning the dark
matter is that it has no significant interactions with other matter,
and that its particles have a negligible velocity as far as structure
formation is concerned. Such dark matter is described as `cold,' and
candidates include the lightest supersymmetric particle, the axion,
and primordial black holes. As far as astrophysicists are concerned, a
complete specification of the relevant cold dark matter properties is
given by the density parameter
c, though
those seeking to directly detect it are as interested in its interaction
properties.
Cold dark matter is the standard assumption and gives an excellent fit to observations, except possibly on the shortest scales where there remains some controversy concerning the structure of dwarf galaxies and possible substructure in galaxy halos. It has long been excluded for all the dark matter to have a large velocity dispersion, so-called `hot' dark matter, as it does not permit galaxies to form; for thermal relics the mass must be above about 1 keV to satisfy this constraint, though relics produced non-thermally, such as the axion, need not obey this limit. However, in future further parameters might need to be introduced to describe dark matter properties relevant to astrophysical observations. Suggestions which have been made include a modest velocity dispersion (warm dark matter) and dark matter self-interactions. There remains the possibility that the dark matter is comprized of two separate components, e.g., a cold one and a hot one, an example being if massive neutrinos have a non-negligible effect.
The number of relativistic species in the young Universe (omitting photons) is denoted Neff. In the standard cosmological model only the three neutrino species contribute, and its baseline value is assumed fixed at 3.046 (the small shift from 3 is because of a slight predicted deviation from a thermal distribution [19]). However, other species could contribute, for example extra neutrino species, possibly of sterile type, or massless Goldstone bosons or other scalars. It is hence interesting to study the effect of allowing this parameter to vary, and indeed although 3.046 is consistent with the data, most analyses currently suggest a somewhat higher value (e.g., Ref. 16).
While the standard cosmological model given above features a cosmological constant, in order to explain observations indicating that the Universe is presently accelerating, further possibilities exist under the general headings of `dark energy' and `modified gravity'. These topics are described in detail in the article by Mortonson, Weinberg and White in this volume. This article focuses on the case of the cosmological constant, as this simple case is a good match to existing data. We note that more general treatments of dark energy/modified gravity will lead to weaker constraints on other parameters.
2.5. Complex ionization history
The full ionization history of the Universe is given by the ionization
fraction as a function of redshift z. The simplest scenario takes
the ionization to have the small residual value left after
recombination up to some redshift zion, at which point the
Universe instantaneously reionizes completely. Then there is a
one-to-one correspondence between
and zion
(that relation, however, also depending on other cosmological
parameters). An accurate treatment of this process will track separate
histories for hydrogen and helium. While currently rapid ionization
appears to be a good approximation, as data improve a more complex
ionization history may need to be considered.
Variation of the fundamental constants of Nature over cosmological times is another possible enhancement of the standard cosmology. There is a long history of study of variation of the gravitational constant GN, and more recently attention has been drawn to the possibility of small fractional variations in the fine-structure constant. There is presently no observational evidence for the former, which is tightly constrained by a variety of measurements. Evidence for the latter has been claimed from studies of spectral line shifts in quasar spectra at redshift z ≈ 2 [21], but this is presently controversial and in need of further observational study.
The usual hypothesis is that the Universe has the simplest topology consistent with its geometry, for example that a flat Universe extends forever. Observations cannot tell us whether that is true, but they can test the possibility of a non-trivial topology on scales up to roughly the present Hubble scale. Extra parameters would be needed to specify both the type and scale of the topology, for example, a cuboidal topology would need specification of the three principal axis lengths. At present, there is no evidence for non-trivial cosmic topology [24].