2. THE EQUATIONS OF COSMIC CHEMICAL EVOLUTION

To pursue and cast light into a quantitative form of the idea of a history of cosmic star formation and metal enrichment - not of any particular type of galaxy but of the Universe as a whole - it is useful to start by generalizing the standard equations of galaxy evolution (Tinsley 1980) over all galaxies and intergalactic gas in the Universe. In a representative cosmological comoving volume with density ρ_∗ in long-lived stars and stellar remnants (white dwarfs, neutron stars, black holes) and gas density ρ_g and in which new stars are formed at the rate ψ, the equations of cosmic chemical evolution can be written as

(1)

Here, Z is the metallicity in the gas and newly born stars, R is the "return fraction" or the mass fraction of each generation of stars that is put back into the interstellar medium (ISM) and intergalactic medium (IGM), and y is the net metal yield or the mass of new heavy elements created and ejected into the ISM/IGM by each generation of stars per unit mass locked into stars. The above equations govern the formation, destruction, and distribution of heavy elements as they cycle through stars and are ultimately dispersed into the ISM/IGM. By treating all galaxies as a single stellar system and all baryons in the ISM/IGM as its gas reservoir, their solution enables the mean trends of galaxy populations to be calculated with the fewest number of free parameters. The equations state that, for every new mass element locked forever into long-lived stars and stellar remnants, Δρ_∗, the metallicity of the ISM/IGM increases as ΔZ = y Δρ_∗ / ρ_g, whereas the mass of heavy elements in the ISM/IGM changes as Δ(Zρ_g) = (y - Z) Δρ_∗. The latter expression is a consequence of metals being released into the gas from mass loss during post-main-sequence stellar evolution as well as being removed from the ISM/IGM when new stars condense out. However, compared with the source term, the metal sink term can be neglected at early epochs when Z ≪ y.

At redshift z, Equation 1 can be integrated to give the following:

1. The total mass density of long-lived stars and stellar remnants accumulated from earlier episodes of star formation,

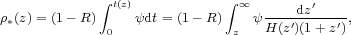   (2)

   where H(z') = H₀[Ω_M(1 + z')³ + Ω_Λ]^1/2 is the Hubble parameter in a flat cosmology.

2. The total mass density of gas,

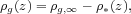   (3)

   where ρ_g,∞ is the comoving density of gas at some suitable high redshift where there are no stars or heavy elements.

3. The total mass density of heavy elements in the ISM/IGM,

   (4)

   where the term < Z_∗> ρ_∗ is the total metal content of stars and remnants at that redshift. Note that the instantaneous total metal ejection rate, E_Z, is the sum of a recycle term and a creation term (Maeder 1992),

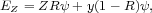   (5)

   where the first term is the amount of heavy elements initially lost from the ISM when stars formed that are now being re-released, and the second represents the new metals synthesized by stars and released during mass loss.

For a given universal stellar IMF, the quantities R and y can be derived using the following formulas:

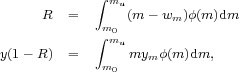(6) (7)

where m is mass of a star, w_m is its remnant mass, ϕ(m) is the IMF [normalized so that ∫_ml^m_u mϕ(m)dm = 1], and y_m is the stellar yield, i.e., the fraction of mass m that is converted to metals and ejected. In this review, the term "yield" generally indicates the net yield y of a stellar population as defined in Equation 7; instead we explicitly speak of "stellar yields" to indicate the y_m resulting from nucleosynthesis calculations. The above equations have been written under the simplifying assumptions of "instantaneous recycling" (where the release and mixing of the products of nucleosynthesis by all stars more massive than m₀ occur on a timescale that is much shorter than the Hubble time, whereas stars with m < m₀ live forever), "one zone" (where the heavy elements are well mixed at all times within the volume under consideration), "closed box" (flows of gas in and out the chosen volume are negligible), and "constant IMF and metal yield."

Recall now that the main-sequence timescale is shorter than 0.6 Gyr (the age of the Universe at z = 8.5) for stars more massive than 2.5 M_⊙, whereas stars less massive than 0.9 M_⊙ never evolve off the main sequence. [Stellar evolutionary models by Schaller et al. (1992) show that, for m < 7 M_⊙, solar-metallicity stars have longer lifetimes than their metal-poor counterparts, whereas the opposite is true for m > 9 M_⊙.] So over the redshift range of interest here, the instantaneous recycling approximation may break down in the limited mass range 0.9 < m < 2.5 M_⊙. For illustrative purposes, in the following we adopt the initial-final mass values for white dwarfs tabulated by Weidemann (2000), which can be fit to few-percent accuracy over the interval 1 M_⊙ < m < 7 M_⊙ as w_m = 0.444 + 0.084m. We also assume that all stars with 8 M_⊙ < m < m_BH = 40 M_⊙ return all but a w_m=1.4 M_⊙ remnant, and stars above m_BH collapse to black holes without ejecting material into space, i.e., w_m = m. Few stars form with masses above 40 M_⊙, so the impact of the latter simplifying assumption on chemical evolution is minimal. Thus, taking m₀ = 1 M_⊙ as the dividing stellar mass for instantaneous recycling and a Salpeter (1955) IMF with ϕ(m) ∝ m^-2.35 in the range m_l = 0.1 M_⊙ < m < m_u = 100 M_⊙, one derives a return fraction of R = 0.27. Under the same assumptions, a Chabrier (2003) IMF,

(8)

(with m_c = 0.08 M_⊙ and σ = 0.69) is more weighted toward short-lived massive stars and yields a larger return fraction, R = 0.41. In the instantaneous recycling approximation, the fraction of "dark" stellar remnants formed in each generation is

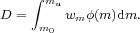(9)

The two IMFs produce a dark remnant mass fraction of D = 0.12 and D = 0.19, respectively. The stellar nucleosynthetic yields depend on metallicity, rotation, and the mass limit for black hole formation m_BH. By integrating over the IMF the subsolar metallicity stellar yields (where the effect of mass loss is negligible) tabulated by Maeder (1992) from 10 M_⊙ to m_BH = 40, M_⊙, we obtain y = 0.016 for a Salpeter and y = 0.032 for a Chabrier IMF. When integrated to m_BH = 60 M_⊙, the same tabulation implies y = 0.023 (with R = 0.29) and y = 0.048 (with R = 0.44) for a Salpeter and Chabrier IMF, respectively. Notice that some of the uncertainties associated with the IMF and the mass cutoff m_BH become smaller when computing the term y(1 - R) in the equations (Equation 1). For massive stars at solar metallicities, stellar winds eject large amount of helium and carbon into the ISM before these are processed into heavier elements, but the effect on the integrated metal yields (10-40 M_⊙) is weak (Maeder 1992). Total stellar yields (including the wind and pre-SN contributions) obtained from rotating stellar models at solar metallicity have been presented by Hirschi et al. (2005). Over the same range 10-40 M_⊙, in this case we derive y = 0.019 for Salpeter and y = 0.038 for Chabrier. For comparison, the zero-metallicity stellar yields of Chieffi & Limongi (2004) imply y = 0.015 for Salpeter and y = 0.030 for Chabrier.

Although disfavored by many observations, a Salpeter IMF in the mass range 0.1-100 M_⊙ is used as a reference throughout the rest of this review. Similarly, for consistency with prior work, we assume the canonical metallicity scale where solar metallicity is Z_⊙ = 0.02, rather than the revised value Z_⊙ = 0.014 of Asplund et al. (2009).