The present-day matter power spectrum is the evolved result of the primordial power spectrum produced during inflation, a period of rapid acceleration in the early Universe. Inflation explains why apparently causally disconnected regions have similar properties, and why the energy-density is close to the critical value, as well as explaining the existence of present-day structure. While the general paradigm of inflation is widely accepted, the details are largely unconstrained (see Byrnes and Choi 2010). Although we know that the post-inflation distribution of fluctuations has a statistical distribution close to a Gaussian (Planck Collaboration et al. 2013a), determining the amount of non-Gaussianity provides a key way of distinguishing between models.
The post-inflation matter power spectrum is commonly parameterised by
a power law, P(k) ∝ kn, where the
power-law index n = 0.96
(Planck
Collaboration et al. 2013b).
This power spectrum is subsequently altered
by physical process within the evolving Universe composed of
radiation, baryons, neutrinos, dark matter and dark energy. In
particular, the relative densities of these components changes with
scale factor a according to the Friedman equation, which for a
CDM Universe can be written in the form
 |
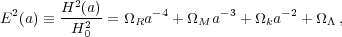(13) |
where E(a) is the Hubble Parameter H(a)
normalised to its present
day value, 
R,
M, and
are the present-day radiation, matter and
densities in
units of the critical density, and
k is the
spatial curvature density (= 1 -
tot).
a is the cosmological scale factor,
a = 1 / (1 + z), such that this equation and the
parameters within can be written as functions of either a or
z. The physics, including the
important processes that are described in the following subsections,
is usually encoded in a transfer function T(k), which
details the change in the power spectrum from the inflationary form
through to the power spectrum in the matter dominated regime (the regime
where the dominant term in Eq. 13 is
M
a-3).
2.1. The matter-radiation equality scale
The growth of dark matter fluctuations is intimately linked to the
Jeans scale. Perturbations smaller than the Jeans scale do not
collapse due to pressure support - for collision-less dark matter
this means being supported by internal random
velocities. Perturbations larger than the Jeans scale grow through
gravity at the same rate, independent of scale. If we approximate the
Universe as containing just dark matter and radiation, the Jeans scale
grows to the size of the horizon at matter-radiation equality, and
then reduces to zero when the matter dominates. We therefore see that
the horizon scale at matter-radiation equality will be imprinted in
the distribution of fluctuations - this scale marks a turn-over in
the growth rate of fluctuations. What this means in practice is that
there is a cut-off in the power spectrum on small scales, dependent on
M
h2. When this scale is observed in
a low-redshift galaxy power spectrum, its position is dependent on
M
h, where h = H0 / 100 km s-1
Mpc-1, as projection
effect introduce another factor of h.
The same principal of gravitational collapse versus pressure support can be applied in the case of massive neutrinos. Initially the neutrinos are relativistic and their Jeans scale grows with the horizon. As their temperature decreases their momenta drop, they become non-relativistic, and the Jeans scale decreases - they can subsequently fall into perturbations. Massive neutrinos are interesting because even at low redshifts the Jeans scale is cosmologically relevant. Consequently the linear power spectrum (the fluctuation distribution excluding the non-linear collapse of perturbations) is not frozen shortly after matter-radiation equality. Instead its form is still changing at low redshifts. Additionally, the growth rate depends on the scale - it is suppressed until neutrinos collapse into perturbations, simply because the perturbations have lower amplitude.
Both the imprint of the matter-radiation equality scale and neutrino masses are further complicated by galaxy bias (see Section 3.4), which limits measurements made from galaxy surveys. However, cosmological neutrino mass measurements are still of strong interest as the standard model of particle physics links together cosmological photon and neutrino species densities: based on current photon density (as measured from the CMB), we expect a cosmological neutrino background with a density 112 cm-3 per species, which leads to an expected cosmological density
 |
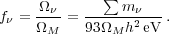(14) |
Thus a measurement of the cosmological density directly gives a measurement of the summed neutrino mass, and has the potential to provide information on the mass hierarchy: Neutrinos come in three flavours, and detectors measure differences among the three mixed states, but the masses themselves are unknown. An interesting question is whether the biggest difference marks the heaviest mixed state (the so-called normal hierarchy) or the lightest one (an inverted hierarchy).
At early epochs baryons are coupled to the photons and are subject to radiation pressure. If we consider a single fluctuation existing after inflation, then a spherical shell of baryonic material and photons is driven away from the perturbation by this pressure. When the photons and gas decouple, a spherical shell of baryons is left around a central concentration of dark matter. As the perturbation evolves through gravity, the density profiles of the baryons and dark matter grow together, and the final perturbation profile is left with a small increase in density in a spherical shell at a radial location corresponding to the sound horizon at the end of the Compton drag epoch rd: this is the radius of the spherical shell (Bashinsky and Bertschinger 2001, Bashinsky and Bertschinger 2002). In order to understand the effect of this process on a field of perturbations, one can imagine many of these superimposed "waves" propagating simultaneously, resulting in a slight preference for perturbations separated by the scale of the sound horizon (perturbations at the original location, and at the spherical shell). When translated into the power spectrum, this becomes a series of oscillations in the same way that the Fourier transform of a top-hat function is a Sinc function.
In addition to these features (called Baryon Acoustic Oscillations, or BAO), fluctuations smaller than the Jeans scale, which tracks the sound horizon until decoupling, do not grow, while large fluctuations are unaffected and continue to grow. The presence of baryons therefore also leads to a reduction in the amplitude of small scale fluctuations. A description of the physics for baryons is given by Eisenstein and Hu (1998) or Appendix A of Meiksin et al. (1999), and a discussion of the acoustic signal in configuration space can be found in Eisenstein et al. (2007b).
In an evolved density field at low redshifts, BAO are damped on small scales due to large-scale bulk flows, which are well described as being random (Eisenstein et al. 2007a). If we write the original power spectrum as Plin(k), and a version without BAO as Pnw(k), then
 |
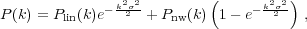(15) |
where 
controls the
amplitude of the damping. The observed
damping is expected to be stronger along the line-of-sight due to the
contribution from Redshift-Space Distortions (see
Section 5.2).