


The tight coupling between radiation and matter density before decoupling caused the primordial adiabatic perturbations to oscillate in phase. Beginning from the time of last scattering, the receding horizon has been revealing these frozen density perturbations, setting up a pattern of standing acoustic waves in the baryon-photon fluid. After decoupling, this pattern is visible today as temperature anisotropies with a certain regularity across the sky.
The primordial photons are polarized by the anisotropic Thomson scattering process, but as long as the photons continue to meet free electrons their polarization is washed out, and no net polarization is produced. At a photon's last scattering however, the induced polarization remains and the subsequently free-streaming photon possesses a quadrupole moment.
Temperature and polarization fluctuations are analyzed in terms of multipole components or powers. The resulting distribution of powers versus multipole ℓ, or multipole moment k = 2 π / ℓ, is the power spectrum which exhibits conspicuous Doppler peaks. In Fig. 12 we display the radiation temperature (TT) and temperature- E-polarization correlation (TE) power spectra from the 7-year data of WMAP as functions of multipole moments [49]. The spectra can then be compared to theory, and theoretical parameters determined. Many experiments have determined the power spectra, so a wealth of data exists.
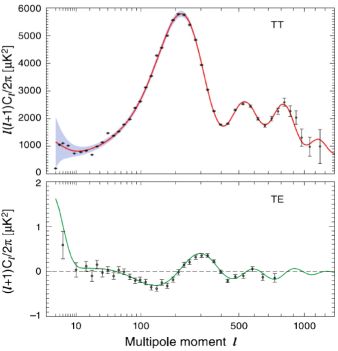 |
Figure 12. The CMB radiation temperature (TT) and temperature-polarization (TE) power spectra from the seven-year WMAP 94 GHz maps.show anisotropies which can be analyzed by power spectra as functions of multipole moments. The solid line shows the best-fit prediction for the flat ΛCDM model. From D. Larson & al. [49] |
Baryonic matter feels attractive self-gravity and is pressure-supported, whereas dark matter only feels attractive self-gravity, but is pressureless. Thus the Doppler peaks in the CMBR power spectrum testify about baryonic and DM, whereas the troughs testify about rarefaction caused by the baryonic pressure. The position of the first peak determines Ωm h2. Combining the TT data with determinations of the Hubble constant h, the WMAP team can determine the total mass density parameter Ωm = Ωb + Ωdm. The ratio of amplitudes of the second-to-first Doppler peaks determines the baryonic density parameter to be Ωb = 0.0449 ± 0.0028 and the dark matter component to be Ωdm = 0.222 ± 0.026 [49], thus Ωm = 0.267.
Power spectra at higher multipole moments have been measured with the Atacama Cosmology Telescope (ACT) [50] at 148 GHz and 218 GHz, as well as the cross-frequency spectrum between these two channels. and found to be in agreement with the 7-year WMAP 94 GHz maps in the common range 400 ≤ ℓ ≤ 1000. The ACT has also been able to measure the lensing of the CMB signal at a significance of 2.8 σ, which slightly smooths out the acoustic peaks, cf Fig. 13.
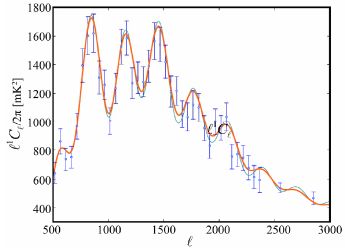 |
Figure 13. The ACT 148GHz power spectrum multiplied by ℓ4 is shown for lensed (orange curve) and unlensed models (green curve). From S. Das & al. [50]. |
In a fit of the flat ΛCDM model to the data the dark matter density parameter comes out slightly higher than WMAP and the baryonic density slightly lower so the total density parameter for WMAP and ACT added is Ωm = 0.276 ± 0.016 [51].
Information on the TE correlations comes from several measurements, among them WMAP [49], and on the E-mode polarization power spectrum alone (EE) from the QUAD collaboration [52], Fig. 14.
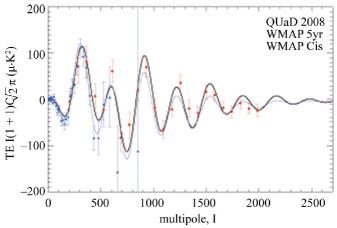 |
Figure 14. The E-mode polarization power spectrum (EE) from the CMB observations of the QUaD collaboration & al. [52] |
The results show two surprises: Firstly, since Ωm ≪ 1, a large component ΩΛ ≈ 0.74 is missing, of unknown nature, and termed dark energy. The second surprise is that ordinary baryonic matter is only a small fraction of the total matter budget. The remainder is then dark matter, of unknown composition. Of the 4.5% of baryons in the Universe only about 1% is stars.