


A cornerstone of cosmology is the Copernican principle, that matter in the Universe is distributed homogeneously, if only on the largest scales of superclusters separated by voids. On smaller scales we observe inhomogeneities in the forms of galaxies, galaxy groups, and clusters. The common approach to this situation is to turn to non-relativistic hydrodynamics and treat matter in the Universe as an adiabatic, viscous, non-static fluid, in which random fluctuations around the mean density appear, manifested by compressions in some regions and rarefactions in other. The origin of these density fluctuations was the tight coupling established before decoupling between radiation and charged matter density, causing them to oscillate in phase. An ordinary fluid is dominated by the material pressure, but in the fluid of our Universe three effects are competing: gravitational attraction, density dilution due to the Hubble flow, and radiation pressure felt by charged particles only.
The inflationary fluctuations crossed the post-inflationary Hubble radius, to come back into vision with a wavelength corresponding to the size of the Hubble radius at that moment. At time teq the overdensities began to amplify and grow into larger inhomogeneities. In overdense regions where the gravitational forces dominate, matter contracts locally and attracts surrounding matter, becoming increasingly unstable until it eventually collapses into a gravitationally bound object. In regions where the pressure forces dominate, the fluctuations move with constant amplitude as sound waves in the fluid, transporting energy from one region of space to another.
Inflationary models predict that the primordial mass density fluctuations should be adiabatic, Gaussian, and exhibit the same scale invariance as the CMB fluctuations. The baryonic acoustic oscillations can be treated similarly to CMB, they are specified by the dimensionless mass autocorrelation function which is the Fourier transform of the power spectrum of a spherical harmonic expansion. The power spectrum is shown in Fig. 15 [53].
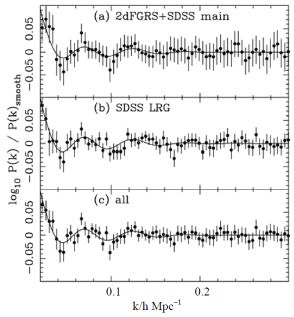 |
Figure 15. BAO in power spectra calculated from (a) the combined SDSS and 2dFGRS main galaxies, (b) the SDSS DR5 LRG sample, and (c) the combination of these two samples (solid symbols with 1σ errors). The data are correlated and the errors are calculated from the diagonal terms in the covariance matrix. A Standard ΛCDM distance–redshift relation was assumed to calculate the power spectra with Ωm = 0.25, ΩΛ = 0.75. From W. J. Percival & al. [53]. |
As the Universe approached decoupling, the photon mean free path increased and radiation could diffuse from overdense regions into underdense ones, thereby smoothing out any inhomogeneities in the plasma. The situation changed dramatically at recombination, at time 380 000 yr after Big Bang, when all the free electrons suddenly disappeared, captured into atomic Bohr orbits, and the radiation pressure almost vanished. Now the baryon acoustic waves and the CMB continued to oscillate independently, but adiabatically, and the density perturbations which had entered the Hubble radius since then could grow with full vigor into baryonic structures.
The scale of BAO depends on Ωm and on the Hubble constant, h, so one needs information on h to break the degeneracy. The result is then Ωm ≈ 0.26. In the ratio Ωb / Ωm the h-dependence cancels out, so one can also quantify the amount of DM on very large scales by Ωb / Ωm = 0.18 ± 0.04.