


Spiral galaxies are stable gravitationally bound systems in which visible matter is composed of stars and interstellar gas. Most of the observable matter is in a relatively thin disc, where stars and gas rotate around the galactic center on nearly circular orbits. The galaxy kinematics is measured by the Doppler shift of well-known emission lines of particular tracers of the gravitational potential: HI, CO and Hα.
If the circular velocity at radius r is v in a rotating galaxy with mass M(r) inside r, the condition for stability is that the centrifugal acceleration v / r should equal the gravitational pull GM(r)/r2, and the radial dependence of v would then be expected to follow Kepler's law
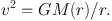 |
(12) |
The surprising result for spiral galaxy rotation curves is, that the velocity does not follow Kepler's inverse-root law, but stays rather constant after attaining a maximum. The most obvious solution to this is that the galaxies are embedded in extensive, diffuse halos of dark matter If the mass M(r) enclosed inside the radius r, is proportional to r it follows that v(r) ≈ constant.
The rotation curve of most galaxies can be fitted by the superposition of contributions from the stellar and gaseous disks, sometimes a bulge, and the dark halo, modeled by a quasi – isothermal sphere. The inner part is difficult to model because the density of stars is high, rendering observations of individual star velocities difficult. Thus the fits are not unique, the relative contributions of disk and dark matter halo is model-dependent, and it is sometimes not even sure whether galactic disks do contain dark matter. Typically, dark matter constitutes about half of the total mass.
In Fig. 3 we show the rotation curves fitted for eleven well-measured galaxies [25] of increasing halo mass. One notes, that the central dark halo component is indeed much smaller than the luminous disk component. At large radii, however, the need for a DM halo is obvious. On galactic scales, the contribution of DM generally dominates the total mass. Note the contribution of the baryonic component, negligible for light masses but increasingly important in the larger structures.
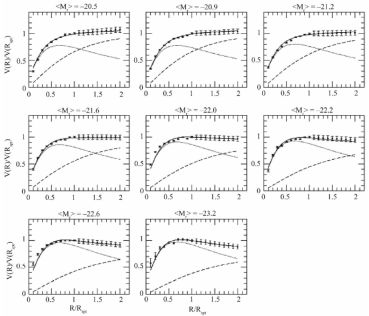 |
Figure 3. Best disk – halo fits to the Universal Rotation Curve (dotted line is disk, dashed line is halo). Each object is identified by the halo virial mass,increasing downwards. From P. Salucci & al. [25]. |
The mass discrepancy emerges also as a disagreement between light and mass distributions: light does not trace mass, the ratio
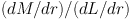 |
(13) |
is not constant, but increases with radius [26].
Gentile & al. [27] have shown that cusped profiles are in clear conflict with data on spiral galaxies. Central densities are rather flat, scaling approximately as ρ0 ∝ rluminous-2/3. The best-fit disk + NFW halo mass model fits the rotation curves poorly, it implies an implausibly low stellar mass-to-light ratio and an unphysically high halo mass. Clearly the actual profiles are of very uncertain origin.
One notes in Fig.3 that the shape of the rotation curve depends on the halo virial mass so that the distribution of gravitating matter, unlike luminous matter, is luminosity dependent. The old idea that the rotation curve stays constant after attaining a maximum is thus a simplification of the real situation. The rotation velocity can be expressed by a Universal Rotation Curve [25]. All spiral galaxies lie on a curve in the 4-dimensional space of luminosity, core radius, halo central density and fraction of DM, see Fig. 4.
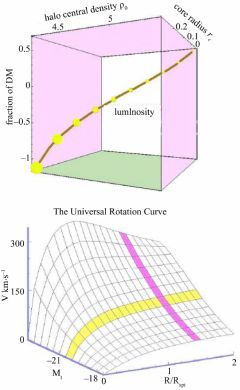 |
Figure 4. Left: The 4-dimensional space of luminosity, core radius, halo central density and fraction of DM. Right: The smooth surface of spiral galaxy rotation curves in the space of normalized radius R/Roptical, magnitude M and rotation velocity V in km s-1. P. Salucci priv. comm. and ref. [25]. |
Our Galaxy is complicated because of what appears to be a noticeable density dip at 9 kpc and a smaller dip at 3 kpc, as is seen in Fig. 5 [28]. To fit the measured rotation curve one needs at least three contributing components: a central bulge, the star disk + gas, and a DM halo [28, 29, 30]. For small radii there is a choice of empirical rotation curves, and no DM component appears to be needed until radii beyond 15 kpc.
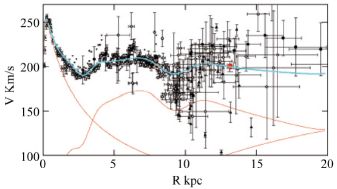 |
Figure 5. Decomposition of the rotation curve of the Milky Way into the components bulge, stellar disk + interstellar gas, DM halo (the red curves from left to right). From Y. Sofue et al. [28]. |