


The planets move around the Sun along their orbits with orbital velocities balanced by the total gravity of the Solar system. Similarly, stars move in galaxies in orbits with orbital velocities v determined by the gravitational field of the galaxy, or they move with velocity dispersion σ. Galaxies in turn move with velocity dispersion σ under the influence of the gravitational field of their environment, which may be a galaxy group, a cluster or a supercluster. In the simplest dynamical framework one treats massive systems (galaxies, groups and clusters) as statistically steady, spherical, self-gravitating systems of N objects with average mass m and average velocity v or velocity dispersion σ. The total kinetic energy E of such a system is then (we now use σ rather than v)
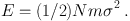 |
(1) |
If the average separation is r, the potential energy of N(N - 1)/2 pairings is
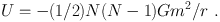 |
(2) |
The virial theorem states that for such a system
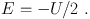 |
(3) |
The total dynamic mass Mdyn can then be estimated from σ and r
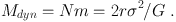 |
(4) |
This can also be written
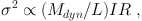 |
(5) |
where I is a surface luminosity, R is a scale, and Mdyn / L is the mass-to-light ratio. Choosing the scale to be the half light radius Re, this implies a relationship between the observed central velocity dispersion σ0, Ie and Re called the Fundamental Plane. of the form
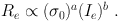 |
(6) |
The virial theorem predicts the values a = 2, b = 1 for the coefficients. This relationship is found in ellipticals [8, 9] and in some other types of stellar populations, but with somewhat different coefficients.
The shapes of DM halos in galaxies and clusters need to be simulated or fitted by empirical formulae. Mostly the shape is taken to be spherically symmetric so that the total gravitating mass profile M(r) depends on three parameters: the mass proportion in stars, the halo mass and the length scale. A frequently used radial density profile parametrization is
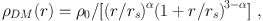 |
(7) |
where ρ0 is a normalization constant and 0 ≤ α ≤ 3/2. Standard choices are α = 1 for the Navarro-Frenk-White profile (NFW) [10], and α = 3/2 for the profile of Moore & al. [11], both cusped at r = 0.
Another parametrization is the Einasto profile ([12] and earlier references therein)
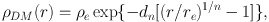 |
(8) |
where the term dn is a function of n such that ρe is the density at re, which defines a volume containing half of the total mass. At r = 0 the density is then finite and cored.
The Burkert profile [13] has a constant density core
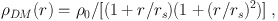 |
(9) |
which fitted dwarf galaxy halos well in 1995, but no longer does so, see Sec. 7.
Some clusters are not well fitted by any spherical approximation. The halo may exhibit a strong ellipticity or triaxiality in which case none of the above profiles is good.
The dependence of the physical size of clusters on the mass, characterized by the mass concentration index c ≡ rvir / rs, has been studied in ΛCDM simulations [14]. At intermediate radii c is a crucial quantity in determining the density shape.
Historically, the first observation of dark matter in an object at a cosmological distance was made by Fritz Zwicky in 1933 [1]. While measuring radial velocity dispersions of member galaxies in the Coma cluster (that contains some 1000 galaxies), and the cluster radius from the volume they occupy, Zwicky was the first to use the virial theorem to infer the existence of unseen matter. He found to his surprise that the dispersions were almost a factor of ten larger than expected from the summed mass of all visually observed galaxies in the Coma. He concluded that in order to hold galaxies together the cluster must contain huge amounts of some non-luminous matter. From the dispersions he concluded that the average mass of galaxies within the cluster was about 160 times greater than expected from their luminosity (a value revised today), and he proposed that most of the missing matter was dark.
Zwicky's suggestion was not taken seriously at first by the astronomical community which Zwicky felt as hostile and prejudicial. Clearly, there was no candidate for the dark matter because gas radiating X-rays and dust radiating in the infrared could not yet be observed, and non-baryonic matter was unthinkable. Only some forty years later when studies of motions of stars within galaxies also implied the presence of a large halo of unseen matter extending beyond the visible stars, dark matter became a serious possibility.
Since that time, modern observations have revised our understanding of the composition of clusters. Luminous stars represent a very small fraction of a cluster mass; in addition there is a baryonic, hot intracluster medium (ICM) visible in the X-ray spectrum. Rich clusters typically have more mass in hot gas than in stars; in the largest virial systems like the Coma the composition is about 85% DM, 14% ICM, and only 1% stars [15].
In modern applications of the virial theorem one also needs to model and parametrize the radial distributions of the ICM and the dark matter densities. In the outskirts of galaxy clusters the virial radius roughly separates bound galaxies from galaxies which may either be infalling or unbound. The virial radius rvir is conventionally defined as the radius within which the mean density is 200 times the background density.
Matter accretion is in general quite well described within the approximation of the Spherical Collapse Model. According to this model, the velocity of the infall motion and the matter overdensity are related. Mass profile estimation is thus possible once the infall pattern of galaxies is known [16].
In Fig. 1 the Coma profile is fitted [15] with Eq. (7) with α = 0 which describes a centrally finite profile which is almost flat. The separation of different components in the core is not well done with Eq. (7) because the Coma has a binary center like many other clusters [17].
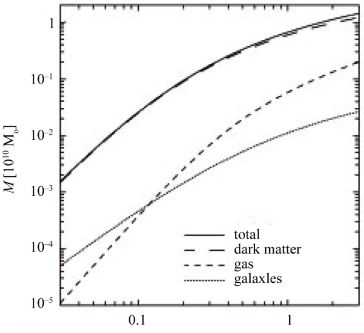 |
Figure 1. Density profile of matter components enclosed within a given radius r in the Coma cluster, versus r / rvir. From E. L. Lokas & G. A. Mamon [15]. |
Dark matter is usually dissected from baryons in lensing analyses by first fitting the lensing features to obtain a map of the total matter distribution and then subtracting the gas mass fraction as inferred from X-ray observations [19, 20]. The total mass map can then be obtained with parametric models in which the contribution from cluster-sized DM halos is considered together with the main galactic DM halos [21]. Mass in stars and in stellar remnants is estimated converting galaxy luminosity to mass assuming suitable stellar mass to light ratios.
One may go one step further by exploiting a parametric model which has three kinds of components: cluster-sized DM halos, galaxy-sized (dark plus stellar) matter halos, and a cluster-sized gas distribution [17, 18]. As an example we show the results of such an analysis of the dynamically active cluster AC 114 in Fig. 2.
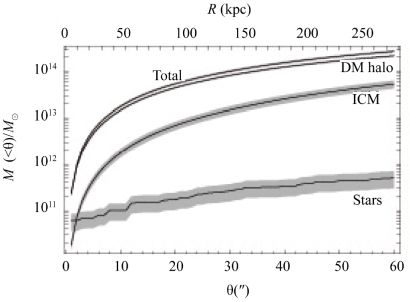 |
Figure 2. Density profile of matter components in the cluster AC 114, enclosed within a given projected radius. From M. Sereno & al. [18]. |
In systems of merging clusters DM may become spatially segregated from baryonic matter and thus observable. We shall meet several such cases in Sec. 15.
The Local Group is a very small virial system, dominated by two large galaxies, the M31 or Andromeda galaxy, and the Milky Way. The M31 exhibits blueshift, falling in towards us. Evidently our Galaxy and M31 form a bound system together with all or most of the minor galaxies in the Local Group. The Local Group extends to about 3 Mpc and the velocity dispersions of its members is about 200 km s-1.
In this group the two large galaxies dominate the dynamics, so that it is not meaningful to define a statistically average pairwise separation between galaxies, nor an average mass nor an average orbital velocity. The total kinetic energy E is still given by the sum of all the group members, and the potential energy U by the sum of all the galaxy pairs, but here the pair formed by the M31 and the Milky Way dominates, and the pairings of the smaller members with each other are negligible.
An interesting recent claim is, that the mass estimate of the Local Group is also affected by the accelerated expansion, the “dark energy”. A. D. Chernin & al. [22] have shown that the potential energy U is reduced in the force field of dark energy, so that the virial theorem for N masses mi with baryocentric radius vectors ri takes the form
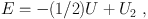 |
(10) |
where U is defined as in Eq. (3), and
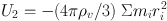 |
(11) |
is a correction which reduces the potential energy due to the background dark energy density ρv. In the Local Group this correction to the mass appears to be quite substantial, of the order of 30% - 50%.
The dynamical mass of the local group is 3.2 - 3.7 × 1012 solar masses whereas the total visible mass of the Galaxy + M31 is only 2 × 1011 solar masses. Thus there is a large amount of dark matter missing.
In a large volume beyond the local group, Tully in 1984 [23] measured the velocities of 2367 galaxies with radial velocities below 3000 km s-1. He found that the mass density parameter (which is normalized to the critical mass) in this "Local Universe" was Ωm = 0.08, in clear conflict with the global value, Ωm,global = 0.27 ± 0.02 (as we shall see in Sec. 14).
More recently Karachentsev [24] has extended this analysis out to a volume of a diameter of 96 Mpc, containing 11 000 galaxies appearing single, in pairs, in triplets and in groups. Most of them belong to the Local Supercluster and constitute < 15% of the mass of Virgo. The radial velocities are v < 3500 km s-1. These galaxies can be treated as a virial system with average density Ωm,local = 0.08 ± 0.02, again surprisingly small compared to the global density. Karachentsev quotes three proposed explanations for this mass deficit.
– Dark matter in the systems of galaxies extends far beyond their virial radius, so that the total mass of a group or cluster is 3 – 4 times larger than the virial estimate. However, this contradicts other existing data.
– The diameter of the considered region of the Local universe, 90 Mpc, does not correspond to the true scale of the "homogeneity cell"; our Galaxy may be located inside a giant void sized about 100 – 500 Mpc, where the mean density of matter is 3 to 4 times lower than the global value. However, the location of our Galaxy is characterized by an excess, rather than by a deficiency of local density at all scales up to 45 Mpc.
– Most of the dark matter in the Universe, or about two thirds of it, is not associated with groups and clusters of galaxies, but distributed in the space between them in the form of massive dark clumps or as a smooth "ocean". It is as yet difficult to evaluate this proposal.
Clearly the physics in the Local Universe does not prove the existence of dark matter, rather it brings in new problems.