


Both “early” bulges and ellipticals follow a common relation, more general than the FJ relation, known as the FP: log Re = α logσ + β logIe + γ, where Re is the effective radius, σ the central velocity dispersion, Ie the effective surface brightness, and α, β, and γ constants (Djorgovski & Davis 1987, Dressler et al. 1987). If the systems are in virial equilibrium (as expected), have a constant M / L, and form a homologous family (i.e. their properties scale simply with luminosity or mass), we expect α = 2 and β = −1 (γ varies with distance). In practice, the coefficients differ from the virial expectation and depend somewhat on their definitions and measurements. Jørgensen, Franx, & Kjærgaard (1996; Fig. 2) obtain α = 1.24 and β = −0.82 in Gunn r, with a scatter of 0.07 in logRe (17% error on individual distances). Crucial for determining distances, the slope is constant among clusters (independent of richness, Tgas, σcluster, etc). The scatter is real, higher for S0s (bulges), and is unlikely due to disks or projection effects (residuals uncorrelated with the shape of the light distribution).
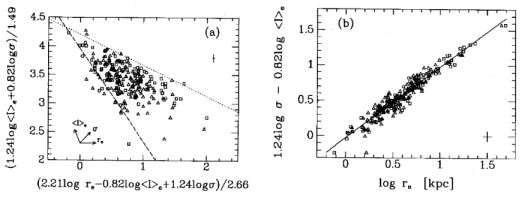 |
Figure 2. Fundamental plane of spheroids in Gunn r. Left: Face-on view. The dashed line represents a selection effect (limiting magnitude), while the dotted line does not. Right: Edge-on view. Boxes: Ellipticals. Triangles: Bulges (S0s). Typical error bars are shown in each panel. Reproduced with permission from Jørgensen et al. (1996). |
Departures from the virial FP can be assigned to a varying mass-to-light ratio, M / L ∝ Re −1−1/β σ2+α / β (M / L∝ Re0.22 σ0.49; Jørgensen et al. 1996). Despite a large scatter, this is an important statement, relating the stellar populations of spheroids to their structural parameters. It is probably unaffected by dark matter, since spheroids appear baryon dominated within one Re (to be contrasted with the Tully-Fisher relation for spirals; Freeman, these proceedings).
A relation between σ and the line-strength index Mg2 (or broadband colors) also exists, varying slightly among clusters, possibly due to age or most likely metallicity variations (Jørgensen et al. 1996). M / L thus varies between clusters (bad for distances if not accounted for), and bulges and ellipticals do not all have the same probability distribution of characteristic parameters. The scatter in the Mg2 “FP” is also real, implying some scatter in the stellar populations.
Although “early” bulges populate the FP slightly differently from ellipticals (as do compact ellipticals, dwarf ellipticals, and dwarf spheroidals), they follow the same Mg2 – σ relation, and their properties again suggests a continuation of the elliptical sequence, indicative to some of a merging sequence with varying degrees of dissipation (see Bender, Burstein, & Faber 1993).