It is fair to say that our basic understanding of the structure and dynamics of bulges and ellipticals stems from work done in the 1970s and early 1980s. A few references will be used to illustrate key developments in the field.
Until the late 1970s, ellipticals and bulges were thought to be very
similar because of similar light profiles, stellar content, and
kinematics. Hints of scaling relations were also beginning to appear.
de Vaucouleurs (1958)
showed that Andromeda's bulge followed the R1/4
surface brightness profile of ellipticals.
Faber (1977)
showed that ellipticals and bulges (S0s and
Ss) had similar stellar populations, sharing the same colors,
Mg2 – MB, and NaD –
Mg2 relations.
Faber & Jackson (FJ;
1976)
discovered a projection of the FP
(L 
σ4), shared by
both ellipticals and bulges (taken here as S0s and M31), and showing
no discontinuity in mass-to-light ratio M / L. Of course,
other properties were known to differ. From their axial ratio distributions,
Sandage, Freeman, &
Stokes (1970)
noted that ellipticals are
consistent with a large range of intrinsic flattening, q ≡
b / a ≈ 1.0 − 0.3, while lenticulars and
spirals must all have intrinsically flat disks, with a nearly constant
axial ratio (q ≈ 0.25). Furthermore, some of the above
similarities were later proven too simplistic.
Because of the flattened light distribution of ellipticals, oblate spheroidal models with isotropic velocity dispersions were first constructed (e.g. Lynden-Bell 1962, Prendergast & Tomer 1970). Wilson (1975) showed that, based on the Ostriker & Peebles (1973) criterion, models flatter than E4 would be unstable to axisymmetric perturbations. The crucial developments, however, came with the first rotation curves based absorption lines, able to probe the stellar kinematics. Illingworth (1977) demonstrated in a distance-independent way that ellipticals have only 1/3 (on average) the rotation required by oblate isotropic models. Rotation thus contributes little to their total kinetic energy. Schechter & Gunn (1979) extended these results and showed that some ellipticals possess significant minor-axis rotation and isophotal twists. It was thus clear that ellipticals were triaxial ellipsoids (or oblate spheroids) flattened by anisotropic velocity dispersions, not rotation. Binney (1976, 1978) had already shown that anisotropies could be preserved in the collapse of a (non-spherical) protogalactic cloud.
These results prompted a new look at bulges. It was quickly realized that many bulges are not well represented by R1/4 light profiles, some even showing an exponential decline (e.g. NGC4565; Jensen & Thuan 1982). Bulges also appeared to be rotating more rapidly than the bright ellipticals studied so far (Kormendy & Illingworth 1982), suggesting formation through dissipational collapse rather than merging (the spin parameter λ is much larger than expected from tidal torques, 0.3 rather than 0.05). Nevertheless, Davies et al. (1983) showed that low luminosity ellipticals rotate as fast, both being consistent with rotationally flattened isotropic oblate models (see Fig. 1). This clearly suggested a continuum in the structure and dynamics of spheroids as the luminosity is decreases.
 |
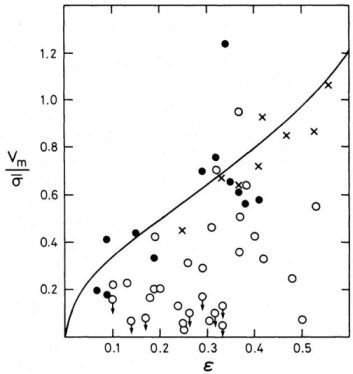Figure 1. Rotational support of
spheroids. The ratio of the maximum
velocity of rotation to the average value of the dispersion within
Re, Vm /
|
Lynden-Bell (1967) provided a physical basis for the aforementioned models, showing that violent relaxation (i.e. rapid collapse) leads to a distribution function f(E, Lz) ∝ exp(−cst.E + cst.Lz), where E and Lz are the specific energy and angular momentum around the symmetry axis, and the Lz term is non-zero for rotating systems only. In fact, for a certain concentration index, King's (1966) models reproduce well the R1/4 law over a large range of radii.
, is plotted as a
function of the projected ellipticity near Re,
є. The solid line represents isotropic oblate rotator models
(