

Although the standard CDM model for dark matter is the best frame to represent the universe at large scales, and account for galaxy formation, it experiences difficulties at galaxy scale (e.g. Moore et al. 1999, Silk & Mamon 2012). Cosmological simulations in the standard model predict an over concentration of dark matter in galaxies, and cuspy density profiles, instead of the density cores derived from rotation curves, especially in low-mass galaxies (e.g. de Blok et al 2008, Swaters et al 2009). Also simulations have difficulties to form large galaxy disks, since the angular momentum of baryons is lost against massive dark halos (e.g. Navarro & Steinmetz 2000), and the missing satellites problem remains unsolved (Diemand et al. 2008). In addition, observed low-mass satellites of the Milky Way have a much larger baryonic fraction than expected from halo abundance matching (e.g. Boylan-Kolchin et al. 2011, 2012).
A large numerical effort has been spent to solve these problems by the detailed physics of the baryonic component, in particular star formation and AGN feedback (e.g. Vogelsberger et al. 2014, Schaye et al. 2015). Another track is to explore alternatives to dark matter models, and in particular modified gravity scenarios, able to account for the missing mass in galaxies.
Already 30 years ago, Milgrom (1983) had the idea of the MOdified Newtonian Dynamics (MOND), based on the fundamental observation that the missing mass problem occurs only in the weak field regime, at low acceleration, when a is lower than the characteristic value of a0 = 2 × 10−10 m/s2. The observed flat rotation curves in the outer parts of galaxies suggests that in this regime the actual acceleration varies in 1/r. Galaxies are also following the baryonic Tully-Fisher relation (McGaugh et al. 2000), where the baryonic mass of a system is proportional to the 4th power of the maximum rotational velocity (see Figure 1). Milgrom then proposes that at acceleration below a0 = 2 × 10−10 m/s2, the gravitational attraction will tend to the formulation a = (a0 aN)1/2, where aN is the Newtonian value. This effectively produces an acceleration in 1/r, implying a flat rotation curve in the limiting regime, and leading automatically to the Tully-Fisher relation. The transition between the Newtonian and MOND regime is controlled by an interpolation function µ(x), of x = a / a0, which standard form is µ(x) = x / (1 + x2)1/2. It essentially tends to x in the MOND regime, when x is smaller than 1, and to unity in the Newtonian regime. This phenomenology has a large success explaining rotation curves and kinematics of galaxies, from dwarf irregulars dominated by dark matter (and therefore in the MOND regime), to the giant spirals and ellipticals, dominated by baryons (e.g. Sanders & McGaugh 2002). Although the model is still empirical, it is possible to build relativistically covariant theories, able to reproduce gravitational lensing and other phenomena, while tending asymptotically to the above formulation in the non-relativistic limit (Bekenstein 2004).
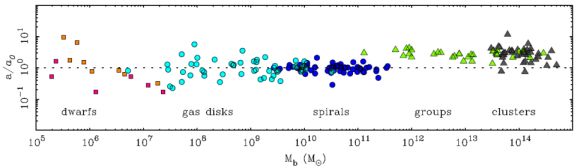 |
Figure 1. The observed parameter Vf4 / (GMb), where Vf is the rotational velocity taken in the flat portion of the rotation curve, and Mb is the baryonic mass, can be also written as the acceleration of the system: a = Vf2 / R, and R = GM / Vf2. The very small deviation of a from the constant a0 is remarkable, given the large range of ten decades in baryonic mass Mb. This observation is somewhat puzzling for the standard dark matter model, but is the basis of the modified gravity (MOND) model (from Famaey & McGaugh 2012). |
The galaxy dynamics is quite different in the MOND hypothesis with respect to the standard dark matter model. Some phenomena have already been explored (see e.g. the review by Famaey & McGaugh 2012), but many are still to be discovered, and in particular galaxy formation, and high redshift evolution. The stability of galaxy disks is fundamentally different, provided that they have low surface brightness (LSB), and are close to the MOND regime (Milgrom & Sanders 2007). Since the MOND disks are completely self-gravitating, they could be much more unstable, however the acceleration is varying asymptotically as the square root of the mass (and not linearly with the mass), so the final effects are not intuitive. Bars are forming quickly in MOND disks, and their pattern speed is not declining through dynamical friciton against a dark matter halo, so resonances are long-lived, and may have more impact (Tiret & Combes 2007). Galaxy interactions with no extended dark halos suffer much less dynamical friction, and mergers are rare (Tiret & Combes 2008b). This changes very significantly the hierachical scenario of galaxy formation, and in particular bulge formation. Therefore, although bulges are now generally in the Newtonian regime today, their formation is certainly very different in the MOND frame with respect to the standard model. Bulges are increasingly important along the Hubble sequence towards the early-types, which correspond to the more massive end. For giant galaxies, the low acceleration regime is encountered only in the outer parts, and the central parts remain Newtonian. Only dwarf galaxies and LSB objects without bulges are still in the MOND regime in their center. This means that bulges today are not likely to be affected by a modified dynamics.
In the following, we will consider in turn the main dynamical mechanisms to form bulges in the ΛCDM paradigm:
Are all these processes also at work in MOND, and with which efficiency? It is well known that the standard ΛCDM model has difficulties to account for the large number of observed bulge-less galaxies (Kormendy et al. 2010). Is this problem solved by MOND?