


This section briefly summarizes the basic notation and geometrical considerations to be used during this chapter.
Let (x, y, z) be the Cartesian coordinates on the reference system of the galaxy with the origin in the galaxy centre, the x−axis and y−axis corresponding to the principal equatorial axes of the ellipsoidal component, and the z−axis corresponding to the polar axis. Therefore, if A, B, and C are the intrinsic lengths of the ellipsoid semi-axes, the corresponding equation of the bulge on its own reference system is given by
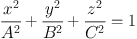 |
(1) |
Let (x′, y′, z′) now be the Cartesian coordinates on the observer reference system. It has its origin in the galaxy centre, the polar z′−axis is along the line of sight (LOS) and points toward the galaxy. (x′, y′) represents the plane of the sky.
The equatorial plane (x, y) of the ellipsoid and the plane of the sky (x′, y′) intersect in the so-called line of nodes (LON). The angle between both planes, i.e., the angle subtended between z and z′ is defined as the inclination θ of the ellipsoid. The remaining two Euler angles which allow for the transformation from the reference system of the galaxy to that of the sky are defined as: i) φ is the angle subtended between the x−axis and the LON in the ellipsoid equatorial plane, and ii) ψ is the angle subtended between the x′−axis and the LON in the plane of the sky. It is often useful to choose the x′−axis to be along the LON, consequently it holds that ψ = 0 (see Figure 1).
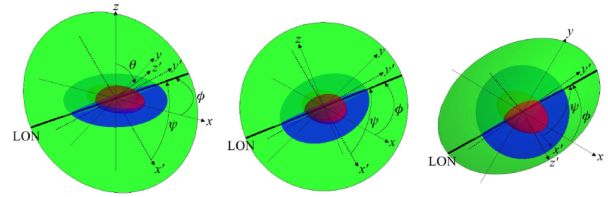 |
Figure 1. Schematic three-dimensional view of the ellipsoid geometry. The bulge ellipsoid, the disc plane, and the sky plane are shown in red, blue, and green, respectively. The reference systems of both the ellipsoid and the observer as well as the LON are plotted with thin solid lines, thin dashed lines, and a thick solid line, respectively. The bulge ellipsoid is shown as seen from an arbitrary viewing angle (left panel), along the LOS (central panel), and along the polar axis (i.e., the z−axis; right panel). Extracted from (Méndez-Abreu et al., 2010). Reproduced with permission from Astronomy & Astrophysics, ⓒ ESO. |
It is well known that the projection of a triaxial ellipsoid onto the plane of the sky describes an ellipse (Contopoulos, 1956, Stark, 1977, Binney, 1985, Franx, Illingworth & de Zeeuw, 1991), which is usually written as
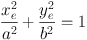 |
(2) |
where xe and ye represent the axes of symmetry of the projected ellipse, a and b are the corresponding semi-major and semi-minor axes of the ellipse. The observed ellipticity of the ellipse can be easily derived from the apparent axis ratio as є = 1 − b / a. The xe axis forms an angle δ with the LON (twist angle), which for convenience is usually made to correspond with the x′-axis. It is worth noting that both the apparent axis ratio (q = b / a) and the orientation of the ellipses (δ) depend only, and unambiguously, on the direction of the LOS, i.e., on θ, φ, and ψ, and on the intrinsic shape of the ellipsoid, i.e., A, B, and C, see Simonneau, Varela & Munoz-Tunon (1998) for the full derivation.
Based on this simple geometric representation, if we assume a galaxy is composed of a set of triaxial emitting ellipsoidal shells, which are concentric and coaxial (same axes of symmetry) but non-homologous (intrinsic semi-axes vary with the distance to the centre), their projections onto the plane of the sky are concentric ellipses, but non-homologous and non-coaxial. Therefore, the twisting of the galaxy isophotes can be explained just as an effect of the projection of non-homologous triaxial ellipsoids (Williams & Schwarzschild, 1979).