


Elliptical galaxies are structurally the simplest stellar systems where mathematical techniques can be applied to recover their intrinsic 3D shape. Thus, the huge amount of literature on the subject is not surprising. In fact, the continuously increasing availability of better measurements of the apparent axis ratios of elliptical galaxies have motivated great debate over the years. On the other hand, the similarities between the photometric properties of intermediate/massive bulges and ellipticals (e.g., Gadotti, 2009) have usually motivated an extrapolation of the results on the intrinsic 3D shape of ellipticals and their implications on galaxy formation and evolution onto the bulges of disc galaxies. In this section I revisit our current knowledge on the intrinsic shape of elliptical galaxies (Sect. 3.1) and, for the sake of completeness, of disc galaxies (Sect. 3.2) to put in context the historical background on the intrinsic shape of bulges.
3.1. Intrinsic shape of elliptical galaxies
The first attempt to derive the intrinsic shape of elliptical galaxies was done by Hubble (1926). At that time, it was already realized the importance of relying on statistical methods to recover the 3D shape of galaxies. In fact, Hubble obtained the frequency of intrinsic short-to-long axis ratio under the assumption that elliptical galaxies were oblate ellipsoids with random orientations with respect to the LOS.
Since then, this statistical approach based on the measurement of the apparent axis ratio distribution (AARD) and the assumption that the 3D intrinsic shape is an ellipsoids of revolution, either oblate or prolate, has been extensively used in the literature. For the sake of clarity I briefly outline here the basic statistical concepts.
Let us assume the basic geometry proposed in Sect. 2 and define both the intrinsic ellipticity, Q = B / A, and intrinsic flattening, F = C / A, of the ellipsoid as the corresponding intrinsic axis ratios in the (x, y) and (x, z) planes, respectively. Therefore, in the case of either a pure oblate (Q = 1) or pure prolate (Q = F) ellipsoid the Eq. 1 can be described by one single parameter. If the polar axis of the ellipsoid forms an angle (θ) with respect to the LOS then the apparent axis ratio of the projected ellipse can be written as
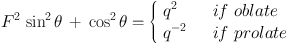 |
(3) |
Under the realistic assumption of randomly distributed orientations and using Eq. 3 where q = q(θ), the probability P(q|F)dq that a galaxy with intrinsic axis ratio F is observed with an apparent axis ratio in the range (q, q + dq) is
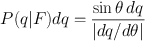 |
(4) |
At this point, the AARD ζ(q), can be related to the intrinsic probability distribution ξ(F) by
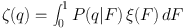 |
(5) |
The relation between the known (observed) frequency of galaxies of apparent axis ratio ζ(q) to the unknown frequency ξ(F) of galaxies with intrinsic axis ratio F can be written such as
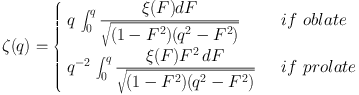 |
(6) |
Based on this approach and using the hypothesis of oblateness, Sandage, Freeman & Stokes (1970) derived the intrinsic distribution of flattening ξ(F) for different Hubble types ranging from ellipticals to Sc. They found that the observed axis ratios of 168 elliptical galaxies present in the Reference Catalog of Bright Galaxies (RC1) (de Vaucouleurs & de Vaucouleurs, 1964) were well reproduced using a skewed binomial distribution of oblate ellipsoids given by
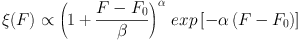 |
(7) |
with main parameters F0 = 0.58 and β = 0.31 (Figure 2, left panels).
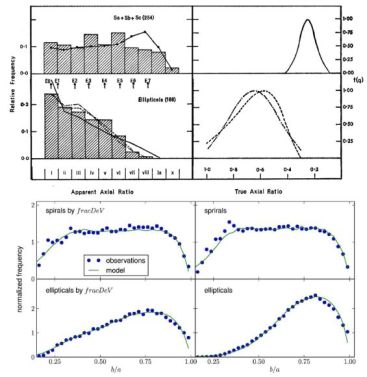 |
Figure 2. Composite figure showing the evolution of the galaxy samples used in the derivation of the intrinsic shape of ellipticals and discs. Upper panels: histograms of the AARD for ellipticals and spiral galaxies. The overplotted curves are predicted ratios for various assumptions of the distribution of intrinsic flattening. On the right, the assumed intrinsic distribution corresponding to the curves on the left. Extracted from Sandage, Freeman & Stokes (1970). Reproduced with permission, ⓒ AAS. Bottom panels: best fit models to AARD compared to the observations. Top: spirals. Bottom: ellipticals. Left: galaxies selected only by fracDeV, see Abazajian et al. (2005) for definition. Right: galaxies selected by Galaxy Zoo morphology and fracDeV. Extracted from Rodríguez & Padilla (2013). Reproduced by permission of Oxford University Press. |
Binney (1978) used the same sample but introducing the prolate approach. Adopting the same functional form for ξ(F) he found values of F0 = 0.40 and β = 0.71. However, even if using arbitrary analytical representations of ξ(F) can turn out in a good fit of the AARD, in principle they do not have a physical motivation. This approximation was improved by Noerdlinger (1979) by solving Eq. 6 using the non-parametric inversion technique proposed by Lucy (1974). His results show how under the hypothesis of oblateness the ξ(F) distribution of Sandage, Freeman & Stokes (1970) was correct, but he also noticed that a prolate distribution peaking at around F ∼ 0.7 would produce a good representation of the data as well.
At the same time, some kinematic findings led to the suggestion that the structure of elliptical galaxies can be represented by neither oblate nor prolate ellipsoids of revolution. In fact, the low ratio between rotational velocity and velocity dispersion found in flat systems (Bertola & Capaccioli, 1975, Illingworth, 1977, Peterson, 1978) or the rotation measured along the minor axis of some elliptical galaxies (Schechter & Gunn, 1979) were interpreted as resulting from a triaxial structure. From the photometric point of view, the twisting of the inner isophotes of elliptical galaxies was known since the early work of Evans (1951) and it was latter confirmed in several works (Liller, 1960, Carter, 1978, Bertola & Galletta, 1979).
As a consequence, Benacchio & Galletta (1980) and Binney & de Vaucouleurs (1981) showed that the AARD could be satisfactorily accounted for also in terms of a distribution of triaxial ellipsoids. Nevertheless, these works still presented significant differences in the predicted number of spherical galaxies mainly due to the differences in the original samples. Other groups reached similar conclusions analysing higher quality data coming from new CCD detectors (Fasano & Vio, 1991).
A new step forward in the methodology to recover the intrinsic 3D shape of galaxies was done by Fall & Frenk (1983). They showed how the inversion of the integral equations for oblate and prolate ellipsoids (Eq. 6) can be performed analytically, resulting in
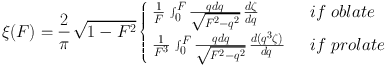 |
(8) |
Using this analytical inversion and the largest sample of galaxies to that date (2135 elliptical galaxies), Lambas, Maddox & Loveday (1992) demonstrated how neither oblate nor prolate models could adequately reproduce the data. Contrarily, triaxial ellipsoids with intrinsic axis ratios selected from 1D Gaussians provided an adequate fit to the data. They found a best fit with Q = 0.95 and F = 0.55. A similar approach was used by Ryden (1992) on a smaller sample of 171 elliptical galaxies. She used a 2D Gaussian combining both intrinsic axis ratios obtaining Q = 0.98 and F = 0.69. The same sample was later analysed by Tremblay & Merritt (1995) using a non-parametric technique to test the triaxial hypothesis. They confirmed previous results that discarded a distribution of intrinsic shapes compatible with axisymmetric ellipsoids thus favouring triaxial distributions. Similar conclusions were reached by Ryden (1996) on a larger sample using the same non-parametric approach.
During these years it became increasingly clear that the distribution of intrinsic flattenings of elliptical galaxies was broad and possibly bimodal (Fasano & Vio, 1991, Ryden, 1992, Tremblay & Merritt, 1995, Ryden, 1996). In fact, combining the galaxy sample described in Ryden (1992) with a new sample of brightest cluster galaxies (BCGs) from Lauer & Postman (1994), Tremblay & Merritt (1996) found that the AARD of galaxies brighter than MB ≃ −20 was different from that of the less luminous ones. This reflected a difference in the shape of low-luminosity and high-luminosity ellipticals: fainter ellipticals are moderately flattened and oblate, while brighter ellipticals are rounder and triaxial. Recently, Fasano et al. (2010) also found that even if both normal ellipticals and BCGs are triaxial, the latter tend to have a more prolate shape, and the tendency to prolateness is mainly driven by the central dominant (cD) galaxies present in their sample.
The next qualitative leap in studies of the intrinsic shape of elliptical galaxies happened with the advent of the Sloan Digital Sky Survey (SDSS). With respect to previous statistical analyses, SDSS improved not only the number of galaxies under study (an order of magnitude larger) but also the quality and homogeneity of the photometry. All these improvements allowed to study the dependence of the intrinsic shape with other galaxy properties such as the luminosity, colour, physical size, and environment. Using data from the SDSS-DR3 (Abazajian et al., 2005) Vincent & Ryden (2005) found that bright galaxies (Mr ≤ −21.84) with a de Vaucouleurs profile have an AARD consistent with a triaxiality parameter in the range 0.4 < T < 0.8, where T = (1 − Q2) / (1 − F2), and mean flattening 0.66 < F < 0.69. The faintest de Vaucouleurs galaxies are best fit with prolate ellipsoids (T = 1) with mean flattening F = 0.51. Using the SDSS-DR5 (Adelman-McCarthy et al., 2007), Kimm & Yi (2007) were able to reproduce the AARD by using a combination of oblate, prolate, and triaxial galaxy populations. Following the early work of Tremblay & Merritt (1996), they assumed each population having a Gaussian distribution of their intrinsic axis ratios. The best fit to the AARD was found using a fraction of O:P:T = 0.29:0.26:0.45 (Oblate:Prolate:Triaxial) with a best triaxial distribution with axis ratios Q = 0.92 and F = 0.78. In 2008, Padilla & Strauss (2008) used the SDSS-DR6 (Adelman-McCarthy et al., 2008) to derive the intrinsic shape of ellipticals with the main improvement of taking into account the effects of dust extinction. They found that the AARD of elliptical galaxies shows no dependence on colour, suggesting that dust extinction is not important for this sample. The full population of elliptical galaxies was well characterized by a Gaussian distribution in the equatorial ellipticity with mean Q = 0.89 and a lognormal distribution of the flattening with mean F = 0.43, which corresponds to slightly oblate ellipsoids in agreement with Vincent & Ryden (2005). In a recent paper, Rodríguez & Padilla (2013) have used the SDSS-DR8 (Aihara et al., 2011) and the morphological information from Galaxy Zoo (Lintott et al., 2011) finding that elliptical galaxies have a mean value of F = 0.58 (Figure 2, right panels). They concluded that the increase in F is mainly due to the removal of the spiral galaxy contamination thanks to the Galaxy Zoo morphologies. A historical summary in tabular form of all these measurements is shown in Table 1.
| Year | N. Galaxies | Hypothesis | Q | F | Reference |
| (1) | (2) | (3) | (4) | (5) | (6) |
| 1970 | 168 | Oblate | 1 | 0.58 | [1] |
| 1978 | 168 | Prolate | 0.4 | 0.4 | [2] |
| 1979 | 168 | Oblate/Prolate | 1/0.7 | 0.55/0.7 | [3] |
| 1980 | 348 | Triaxial | 0.81 | 0.62 | [4] |
| 1981 | 196 | Oblate/Prolate/Triaxial | 1/0.62/0.79 | 0.62/0.62/0.57 | [5] |
| 1992 | 2135 | Triaxial | 0.95 | 0.55 | [6] |
| 1992 | 171 | Triaxial | 0.98 | 0.69 | [7] |
| 2005 | 26994 | Triaxial | 0.66-0.85 | 0.66-0.69 | [8] |
| 2007 | 3922 | Oblate/Prolate/Triaxial | 1/0.72/0.92 | 0.44/0.72/0.78 | [9] |
| 2008 | 303390 | Triaxial | 0.89 | 0.38 | [10] |
| 2013 | 112100 | Triaxial | 0.88 | 0.58 | [11] |
| Notes. (1) Year of publication of the paper. (2) Number of elliptical galaxies in each sample. (3) Hypothesis used to derive the intrinsic shape of the ellipticals. (4) Mean value of the intrinsic ellipticity. (5) Mean value of the intrinsic flattening. (6) Reference of the corresponding paper: [1] Sandage, Freeman & Stokes (1970), [2] Binney (1978), [3] Noerdlinger (1979), [4] Benacchio & Galletta (1980), [5] Binney & de Vaucouleurs (1981), [6] Lambas, Maddox & Loveday (1992), [7] Ryden (1992), [8] Vincent & Ryden (2005), [9] Kimm & Yi (2007), [10] Padilla & Strauss (2008), [11] Rodríguez & Padilla (2013). | |||||
Owing to the ill-posed problem of deriving the 3D intrinsic shape of elliptical galaxies, its historical perspective is mainly weighted toward statistical methods. As previously showed in this section, the inventiveness of astronomers, the development of statistical methods, and the advent of large surveys have significantly improved our knowledge of the intrinsic shape of elliptical galaxies. Other methods based on the photometric study of individual galaxies have also been developed but to a smaller extent. One of the pioneering works to derive the intrinsic shape of an individual elliptical using its observed ellipticity and isophotal twist was done by Williams (1981). They modelled the elliptical galaxy NGC 0523 assuming a given intrinsic density distribution and finding that the preferred models were prolate in the external regions but increasingly mixed (oblate and prolate) towards the centre. This idea was further developed by other authors using more complex models of the density distribution (Fasano, 1995, Thakur & Chakraborty, 2001). In 2008, Chakraborty, Singh & Gaffar (2008) estimated the shapes of 10 elliptical galaxies with apparent ellipticities є ≤ 0.3, finding that radial differences in the triaxiality parameter can be tightly constrained to values 0.29 < ΔT < 0.54. Chakraborty, Diwakar & Pandey (2011) extended this analysis to 3 very flat galaxies with ellipticity є ∼ 0.3 or more. They found values of the intrinsic flattening of these galaxies around F ∼ 0.5.
Determining the distribution of the 3D intrinsic shape of elliptical galaxies is also possible by combining photometric and kinematic information. In a first attempt, Binney (1985) used simple kinematical models to understand the ratio of rotational motion along both the major and minor isophotal axes of the galaxy. Using a sample of 10 ellipticals he found that elliptical galaxies were not well represented by axisymmetric oblate or prolate models. Franx, Illingworth & de Zeeuw (1991) revisited this approach by using a larger sample of 38 elliptical galaxies and studying the probability distribution of photometric ellipticities and kinematics misalignments. In particular, they explored the possibility that the angular momentum could not be aligned with the polar axis of the galaxy but it may have any orientation within the plane containing the short and the long axis (x, z). They found that a variety of models was able to reproduce the observations. Models with all galaxies being triaxial with well-aligned angular momentum were indistinguishable from models with all galaxies being oblate with nonaligned angular momentum.
A different standpoint to statistical studies implies an investigation into the intrinsic shape of elliptical galaxies using detailed individual dynamical modelling of the galaxy kinematics. Tenjes et al. (1993) modelled the photometric and stellar kinematic measurements of three elliptical galaxies adopting a specific form for the intrinsic density and streaming motions. They found tightly constrained geometries with 0.7 < Q < 0.8 and 0.4 < F < 0.6. This methodology was further improved in a series of papers by Statler (Statler, 1994a, Statler & Fry, 1994, Statler, 1994b). He showed how using not only their apparent shapes and velocity field misalignments, but also the velocity field asymmetry, it is possible to place tighter constraints on the intrinsic shape of ellipticals. Using this approach Bak & Statler (2000) derived the intrinsic shape of 13 elliptical galaxies finding that although photometric studies give similar results for the flattening, none is able to put real constraints on triaxiality even when large samples are studied, hence demonstrating the need to include kinematic data in the models. Figure 3 show the probability distribution of intrinsic axis ratio for 9 galaxies with significant rotation in their sample. It is clear that most of the galaxies can be well described by nearly oblate models but some of them present significant triaxiality or even prolateness. van den Bosch & van de Ven (2009) investigated how well the intrinsic shape of elliptical galaxies can be recovered by fitting realistic triaxial dynamical models to simulated photometric and kinematic observations. They found that for axisymmetric galaxies, the models are able to exclude triaxiality but the intrinsic flattening is nearly unconstrained. On the other hand, the shape of triaxial galaxies can be accurately determined when additional photometric and kinematic complexity, such as the presence of isophotal twist or a kinematically decoupled core is observed.
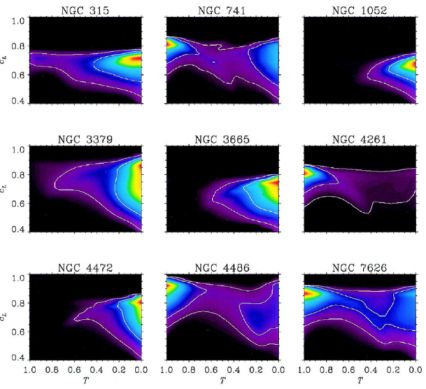 |
Figure 3. Posterior probability densities in the plane of intrinsic triaxiality, T, and flattening, cL (F in this chapter), for each of the nine galaxies that show significant rotation in Bak & Statler (2000). Contours indicate the 68% and 95% highest posterior density regions. In each panel, round prolate galaxies are at the top left, flattened oblate galaxies at bottom right, and objects in between are triaxial. Most galaxies are well represented by oblate models but prolate and triaxial are also allowed in many galaxies, e.g., NGC 741, NGC 4486, or NGC 7626. Extracted from Bak & Statler (2000). Reproduced with permission, ⓒ AAS. |
Recently, Weijmans et al. (2014) studied the intrinsic shape of the early-type galaxies described in the ATLAS3D survey (Cappellari et al., 2011). Using a purely photometric approach and assuming axisymmetry, they found that the fast rotator population was much flatter than the slow rotator population, as expected from their dynamical status. Moreover, when the kinematic misalignment is included as a constraint in the analysis, they demonstrated that fast rotators are still better represented to oblate ellipsoids.
3.2. Intrinsic shape of disc galaxies
In this section I briefly summarise our current understanding about the intrinsic 3D shape of discs. Bulges are embedded into the disc light and axisymmetry is usually a requirement to derive the bulge intrinsic shape. However, although the discs of lenticular and spiral galaxies are often considered to be infinitesimally thin and perfectly circular, their intrinsic shape is better approximated by flattened triaxial ellipsoids.
The disc flattening, defined analogously as for ellipticals (Sect. 3.1), can be directly determined from edge-on galaxies. It depends both on the wavelength at which discs are observed and on galaxy morphological type. Indeed, galactic discs become thicker at longer wavelengths (Dalcanton & Bernstein, 2002, Mitronova et al., 2004) and late-type spirals have thicker discs than early-type spirals (Bottinelli et al., 1983, Guthrie, 1992).
Determining the distribution of both the intrinsic flattening and ellipticity of discs is possible by a statistical analysis of the AARD of randomly oriented spiral galaxies. Similarly for elliptical galaxies, Sandage, Freeman & Stokes (1970) analysed the spiral galaxies listed in the RC1. They concluded that discs are circular with a mean flattening of ⟨ F ⟩ = 0.25. However, the lack of nearly circular spiral galaxies (q ≃ 1) rules out that discs have a perfectly axisymmetric shape. Indeed, Binggeli (1980), Benacchio & Galletta (1980), and Binney & de Vaucouleurs (1981) have shown that discs are slightly elliptical with a mean intrinsic ellipticity ⟨ 1 − Q ⟩ = 0.1. These early findings were based on the analysis of photographic plates of a few hundreds of galaxies. They were later confirmed by measuring ellipticities of several thousands of objects in CCD images and digital scans of plates obtained in wide-field surveys. Lambas, Maddox & Loveday (1992) found that pure oblate models failed to reproduce the AARD of spiral galaxies, whereas nearly oblate models with F ∼ 0.2 and Q ∼ 0.9 produce a good fit with values similar to those of Sandage, Freeman & Stokes (1970). These values were confirmed later on by different authors (Fasano et al., 1993, Alam & Ryden, 2002, Ryden, 2004). Like the flattening, the intrinsic ellipticity depends on the morphological type and wavelength. The discs of early-type spirals are more elliptical than those of late-type spirals and their median ellipticity increases with observed wavelength (Ryden, 2006). Furthermore, luminous spiral galaxies tend to have thicker and rounder discs than low-luminosity spiral galaxies Padilla & Strauss (2008). In Sánchez-Janssen, Méndez-Abreu & Aguerri (2010) they studied the role of stellar mass in shaping the thickness of galaxy discs. They found that the intrinsic thickness distribution of discs has a characteristic U-shape and identify a limiting mass M⋆ ≈ 2 × 109 M⊙ below which low-mass galaxies start to be systematically thicker. Recently, Rodríguez & Padilla (2013) analyse a sample of 92923 spiral galaxies extracted from the SDSS-DR8, and taking into account the effects of dust in their analysis, they found a distribution of flattening with mean F = 0.27 and ellipticity Q = 0.22, i.e., disc are less round than in previous studies (Figure 2, right panels).
Despite the large effort made to understand the intrinsic 3D shape of galaxy discs, it is still unclear whether the inferred slight triaxiality could be due to the presence of substructure in galaxy discs or if it really reflects truly triaxial potential in spirals.