


The first studies of stellar populations in bulges were performed using optical and near-infrared broadband photometry (Balcells & Peletier 1994, Terndrup et al. 1994, Peletier & Balcells 1996, Bell & de Jong 2000, de Jong 1996). These works demonstrated that changes in the bulge colors are linked to galaxy luminosity, potential well, and local surface brightness, with more massive/luminous bulges and higher surface brightness regions being redder than less massive/luminous and lower surface brightness ones. They also showed that early-type bulges are red, as red as elliptical galaxies, and with very little dispersion in their colors (Peletier & Balcells 1996). These results do not apply to the few late-type galaxies analyzed, where significantly bluer colors are measured.
Early interpretation of these data pointed to early-type bulges being as old as ellipticals with late-type, less massive ones being younger and/or more metal poor. The small dispersion in the colors was interpreted as being due to small dispersion in the age of early-type bulges (maximum of ∼2 Gyr). This, in principle, is in agreement with the classical and disky bulge formation scenarios (see Sect. 1) if, as it seems the case, secularly formed disky bulges are more common in late-type and in less massive galaxies (Kormendy & Kennicutt 2004, Ganda et al. 2009) 1.
One problem of using colors is the well known age-metallicity degeneracy (Worthey 1994). Bluer bulges can be either younger or more metal poor and, without this information, it is difficult to extract conclusions about their formation mechanisms. Further complications are the presence of emission lines and dust extinction that also affect the colors. In particular, dust extinction depends on the inclination and, therefore, inclination is another parameter that needs to be taken into account when comparing the colors of different types of bulges and also when comparing the results from different studies (see Ganda et al. 2009). All these obstacles make very difficult to extract useful conclusions about the stellar populations of bulges using only colors. For these reasons studies with colors need to be complemented with those using information of the absorption lines with different sensitivities to age and metallicity and that are not affected by dust extinction (MacArthur 2005).
The first spectroscopic studies of bulges analyzed the relation of line-strength indices (the so-called Lick/IDS indices, see Gorgas et al. 1993, Worthey et al. 1994) with the central velocity dispersion (σ hereafter) – used as a proxy for the dynamical mass of the galaxy. Lick/IDS indices measure the strength of the most prominent absorption lines in the optical galaxy spectra and are sensitive to changes of the mean age, chemical abundances and, to a lesser extent, the initial mass function (e.g. Vazdekis et al. 2010, Bruzual & Charlot 2003, Thomas et al. 2003, Schiavon 2007, Conroy & van Dokkum 2012). These studies confirmed the similarity of bulges with elliptical galaxies for early-type galaxies (earlier than Sbc, Bender et al. 1993, Fisher et al. 1996, Idiart et al. 1996).
However, it has been pointed out that this similarity may be due to the fact that the majority of these early analyses were performed on samples that are biased towards early-type spirals (earlier than Sbc, Kormendy & Kennicutt 2004). In the last few years, however, several studies have included in their samples late-type bulges and analyzed, mostly, the relation between the Mg-sensitive indices (Mg2 and Mgb) and the central σ. When these bulges were included, differences between elliptical and bulges were found. However, the nature of these differences is still not clear. Some authors claim that bulges are located below the Mg-σ relation obtained for ellipticals, which is commonly interpreted as bulges having a younger stellar population (Prugniel et al. 2001, Chiappini et al. 2002, Ganda et al. 2007, Morelli et al. 2008). Other authors find that the slope of the Mg-σ is steeper for bulges (Falcón-Barroso et al. 2002), while Trager et al. (1999) and Proctor & Sansom (2002) report that only low-mass bulges depart from the relation between spectral indices and σ drawn by large bulges. On the other hand, other studies do not find any systematic difference in the Mg-σ relation of bulges and elliptical galaxies but find that the scatter among this relation for bulges is larger than the equivalent one for ellipticals (Moorthy & Holtzman 2006, Peletier et al. 2007). Similar conclusions were obtained using other line-strength indices.
Some of the discrepancies in the conclusions of different studies may be due to differences in the mass distribution (or central σ) of the selected sample. For example, Fig. 1 shows the relation between the Mgb and Hβ indices (measured in magnitudes) for a sample of late-type and early-type bulges and elliptical galaxies from Ganda et al. (2007). It can be seen that despite the relations between line-strength and indices followed by late-type bulges and early-type galaxies running apparently parallel to each other, the differences may just be related with the different range of central σ. In fact, the differences disappear at low-σ, where even early-type galaxies (E and S0 2) deviate from the relation defined by massive ellipticals.
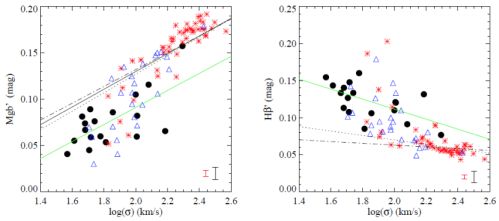 |
Figure 1. Line-strength indices Mgb′ and Hβ ′ expressed in magnitudes, against central velocity dispersion. The black symbols represent the sample of late-type bulges from Ganda et al. (2007), and the blue and the red symbols, the sample of Sa galaxies and E and S0 respectively from the SAURON survey. The dotted and dashed-dotted black lines over-plotted in both panels are the relations obtained by Sánchez-Blázquez et al. (2006a) for low- and high-density environments, respectively, and the green solid lines are the relations determined using the late-type galaxy sample. Representative error bars are added at the bottom right of each panel; the black one refers to both the early- and late-type spiral samples, while the red one refers to the E/S0 galaxies. Figure taken from Ganda et al. (2007). |
Furthermore, bulges, contrary to massive elliptical galaxies, are rotationally supported. Some authors have cautioned (Prugniel & Simien 1994, Falcón-Barroso et al. 2002) that by not taking into account the rotation in the σ measurements, one may be underestimating their binding energy. The contribution to the rotation may by calculated as 0.5 log(1 + 0.62 V2 / σ2), as in Prugniel & Simien (1994), where V is the rotational velocity. Falcón-Barroso et al. (2002) claim that a mean V/σ = 0.5 suffices to bring the bulges back to the Mg2-σ relation defined by giant ellipticals 3. Other studies have also claimed a better correlation between the line-strength indices and Vmax (an indicator of the total potential well) than between line-strength indices and the central σ (Prugniel et al. 2001).
2.2. Comparison with SSP models
Nevertheless, the similarity found by some authors between the index-σ relation of bulges and elliptical galaxies may not reflect a real similarity in their stellar content. Line-strength indices are not free from the age-metallicity degeneracy (e.g., Mg2 and Mgb can be lower in younger or in more metal stellar populations). Therefore, large differences between the ages of bulges and ellipticals could exist and not be reflected in these relations if there is a complementary age-metallicity relation (e.g. Trager et al. 2000). The advantage of using these characteristics, though, is that the sensitivity to variations of age and metallicity of each different index varies. A way to partially break the age-metallicity degeneracy is to combine indices more sensitive to mean age variations (i.e., the Balmer lines) with those more sensitive to abundance variations in the so-called index-index diagrams. Figure 2 shows one of these diagrams combining the composite index
 |
which is fairly insensitive to variations of [α / Fe] abundances 4 (Thomas et al. 2003) and the Balmer index Hβ.
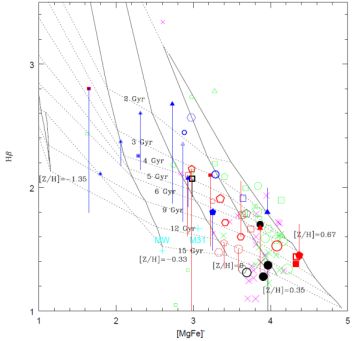 |
Figure 2. Hβ vs. [MgFe]′ in the central regions of bulges and ellipticals. Magenta crosses are galaxies from Trager et al. (1999). Green symbols are bulges and ellipticals from Proctor & Sansom (2002). The MW (Puzia et al. 2002) and M31 (Puzia et al. 2005) are shown as ’+’ symbols. Blue and red symbols are from Moorthy & Holtzman (2006). The color of the symbol is chosen according to whether they are redder or bluer than B - K = 4. Larger sizes indicate larger central velocity dispersion. Bulges for which there is no color information are in black. Solid lines represent the predictions of Thomas et al. (2003) for SSPs of constant metallicity (as indicated in the labels) while dotted lines represent the predictions for populations of constant age, with age increasing towards the bottom of the panel. For other details regarding the figure see Moorthy & Holtzman (2006). |
Several authors have used this technique to compare the index values with the predictions of SSP models. These comparisons show that bulges have a large range in SSP-equivalent ages from ∼ 2 to 13.5 Gyr (Peletier et al. 2007, Moorthy & Holtzman 2006) and metallicities. They also report a correlation between both the SSP-equivalent age and metallicity and central σ. In general, they found that more luminous/massive bulges were older and more metal rich. They also inferred that more massive bulges have a larger ratio of α-elements 5 with respect to Fe, which is usually interpreted as more massive bulges forming their stars on shorter timescales. The relations were similar to those found for elliptical galaxies (Bica 1988, Jablonka et al. 1996, Idiart et al. 1996, Casuso et al. 1996, Goudfrooij et al. 1999, Trager et al. 1999, Thomas & Davies 2006, Moorthy & Holtzman 2006, Jablonka et al. 2007, Ganda et al. 2007). On the other hand, Proctor & Sansom (2002) and Prugniel et al. (2001) found that, contrary to what happens in elliptical galaxies, both Fe and Mg were correlated with σ in bulges, resulting in the lack of a tight correlation between Mg/Fe (a proxy for [α / Fe]) and σ. This result needs to be corroborated by other studies.
Similar to the results obtained with line-strength indices, the comparison of SSP-equivalent parameters of bulges and ellipticals reveal that both have very similar properties, at least in samples of bulges earlier than Sbc. Figure 3 illustrates the relation between the SSP-equivalent ages, metallicities, and [α / Fe], and the central σ for bulges, S0, and elliptical galaxies (Thomas & Davies 2006). It can be seen that, at a given central σ, the stellar population parameters of bulges and elliptical galaxies are indistinguishable. These results support the idea that bulges (with morphological types earlier than Sbc) were formed with very little influence from the disk, in a process similar to the one that formed elliptical galaxies.
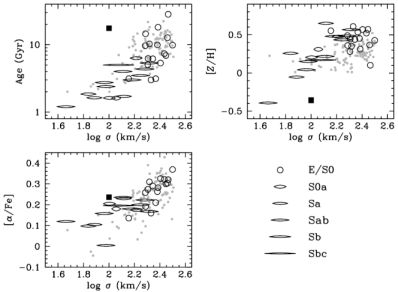 |
Figure 3. Stellar population parameters versus central velocity dispersion. Open circles are early-type galaxies from Thomas & Davies (2006), ellipses are spiral bulges with ellipticity increasing for the later-types (see labels in the right-hand bottom panel) and the filled square is the integrated light of the MW bulge. Small grey-filled circles are early-type galaxies from Thomas et al. (2005). Central stellar populations are shown. Figure taken from Thomas & Davies (2006). |
In samples that contained late-type galaxies (later than Sbc), both Prugniel et al. (2001) and Moorthy & Holtzman (2006 (see also Morelli et al. 2008) find three types of bulges in the comparison of line-strength indices and stellar population models: the old-metal rich (OMR), the young metal rich (YMR) – which are bulges with ages less than 3 Gyr and super-solar metallicities – and the metal poor (MP), with sub-solar metallicity. These classes seem to be sensitive to the Hubble type. All the early-type (S0-Sab) bulges are metal-rich. The red early-type bulges are in the OMR region while the blue early-types reside in the YMR region. Metal-poor bulges are all late-types, but late-type bulges are found in all three regions. A comparison of the SSP properties of late-type bulges and ellipticals galaxies at a similar σ, however, remains to be done and, therefore, as it was the case with the line-strength indices, it is not clear if late-type bulges are younger, for being late-type, or for having low σ.
2.3. Relation between stellar population and structural properties
A more direct way to test the different proposed scenarios for bulge formation is to compare the stellar population properties of a sample of bulges with morphological or dynamical properties that distinguish them as classical, disky, and boxy/peanut. As we have seen in previous chapters (see Chapter 2.2), there are several observables used to separate bulges and pseudobulges and different authors have employed different properties to perform this task. Carollo et al. (2001) analyzed V, H, and J HST images of a sample of bulges with exponential (typical of disky and boxy/peanut bulges) and R1/4 luminosity profiles (typical of classical bulges), finding the former, on average, bluer than the latter (by ∼ 0.4 mag in <V − H>), which could be the consequence of a younger and/or of a lower metallicity stellar population. They also found, in agreement with the results of Peletier & Balcells (1996), that the colors of those bulges showing a R1/4 profile were red and very homogeneous, while for the exponential bulges the scatter was significantly larger 6. They interpreted these results as a delayed formation of the exponential bulges compared with those having an R1/4 profile, which formed their stars in the early Universe. Drory & Fisher (2007) used a different approach and separated classical and pseudobulges morphologically. Pseudobulges were those showing nuclear bars, nuclear spirals, and/or nuclear rings and classical bulges those featureless structures rounder than the outer disk. Separating the bulges in this way and comparing with their visual morphological types, they studied the location of bulges in the color-magnitude diagram, finding that Sc galaxies and later types do not contain classical bulges and are located almost entirely in the blue cloud in the color-magnitude diagram. Intermediate Sa-Sbc type galaxies, on the contrary, contain both classical and pseudobulges. While 87% of the galaxies with pseudobulges were in the blue cloud, all galaxies with classical bulges were in the red-sequence. These authors stress that the differences in colors are not due to a different contribution of bulge and disk to the total galaxy color as blue and red galaxies share a range in bulge-to-total ratio. This is shown in Fig. 4, where the global color of the galaxies is plotted as a function of the bulge-to-total (B/T) ratio. It can be seen that both bulges and pseudobulges coexist in the region of B/T values ranging from 0.05 to 0.45 and that, in this region, classical bulges are redder than pseudobulges. They also found that, in general, pseudobulges classified with the morphological features described above were more diffuse and had lower Sérsic indices than classical bulges.
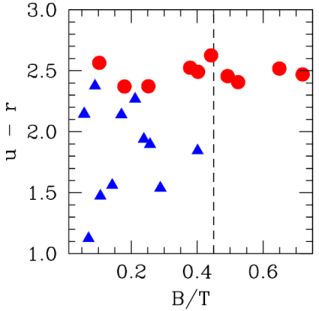 |
Figure 4. Distribution of bulge-to-total ratios, B/T, of intermediate type (Sa-Sbc) galaxies with pseudobulges (blue triangles) and classical bulges (red circles) with respect to their global u-r color. The dashed line marks B/T = 0.45 above which only classical bulges are found. From Drory & Fisher (2007). |
Another way of separating classical bulges from pseudobulges was adopted by Gadotti (2009) who identified pseudobulges as those lying below the Kormendy relation (Kormendy 1977) defined by elliptical galaxies. He established that pseudobulges defined this way were, in general, 0.2 mag bluer in the (g − i) color than the classical bulges. On the other hand, Fernández Lorenzo et al. (2014), who used the Sérsic index to differentiate between classical and pseudobulges, found the latter as red as the former at the same luminosity. Only in fainter pseudobulges they did measure bluer colors.
Again, colors are affected by the age-metallicity degeneracy and dust extinction and, in principle, more information may be obtained from the study of absorption lines and their comparison with stellar population models. Several works have also compared the line-strength indices of bulges with different structural characteristics (Williams et al. 2012, Gadotti 2009). The first studied a sample of edge-on boxy/peanut bulges finding that they follow the same central index-σ relation as elliptical galaxies (see also Jablonka et al. 2007), although the sample was biased towards early-type galaxies (S0-Sb). On the other hand, Gadotti (2009) found a strong correlation between the D4000 index and the Sérsic index (n), indicating younger populations 7 in galaxies with lower n. On the contrary, for a sample of early-type galaxies, Vazdekis et al. (2004) did not find a correlation between n and age, while they found a strong correlation between n and [Mg/Fe]. The different behavior for bulges and ellipticals is very interesting, but more studies of this kind using larger samples are still needed to confirm or refute the trends. Note that the only study targeting specifically boxy/peanut bulges is that of Williams et al. (2012). The rest of studies cited above usually include both disky and boxy/peanut bulges in the same category, the ‘pseudobulge’ sample.
The current lack of consensus between studies may be due to different criteria to separate classical and pseudobulges. Some might include disky and boxy/peanut bulges in the same category, pseudobulge, without making any distinction between them. Furthermore, different distributions of the galaxy luminosities can also lead to discordant results. It is clear that low-luminosity, low-mass bulges are bluer than more massive and brighter ones, but it is not clear if, at the same luminosity, bulges with different structural characteristics share the same color.
2.4. Bulges as composite systems
Thanks to the 2-dimensional data of the SAURON survey (Bacon et al. 2001), Peletier et al. (2007) (see also Sil’chenko & Afanasiev 2004) noticed that, when present, young stellar populations in their sample of early-type bulges were concentrated near the center, in disks or in annuli suggestive of resonance rings (Byrd et al. 1994). Peletier et al. (2007) realized that the studies comparing the line-strength indices of bulges and elliptical galaxies could be divided into two categories: those targeting inclined galaxies, which do not find any difference between the index-σ relation of bulges and ellipticals, and those sampling almost face-on galaxies, which find younger stellar populations in bulges compared with those of elliptical galaxies and a large scatter in the line-strength indices at a given σ. The differences are especially visible in galaxies with low σ. They argue that bulges are composite systems, with two or more types of bulges coexisting in the same galaxies. The classical bulge is composed mainly of an old and metal rich population and the disky and boxy/peanut bulge can be younger and contain more metal-poor stars (although it can also be old). The discrepant results obtained in samples of different inclinations can be explained, according to these authors, by the different contribution to the bulge light of different subcomponents (classical, disky, and boxy/peanut). If the young component is a disk, then it is concentrated in a plane and it would not be observed in edge-on galaxies. These young components, however, do contribute to the integrated light of less inclined samples (if they are limited to the central regions). The result is supported by the observation of central dips in the velocity dispersion maps in 50% of the galaxies of their sample.
The coexistence of 2 or more types of bulges (classical, disky, and boxy/peanut) in some galaxies has been pointed out by several authors (Athanassoula 2005, Gadotti 2009, Nowak et al. 2010, Kormendy & Barentine 2010, Erwin 2008) and is supported by theoretical studies (Obreja et al. 2013, Samland & Gerhard 2003). Obreja et al. (2013) propose a picture were the centers of most early-type spirals contain multiple kinematic components: an old and slowly rotating elliptical-like component, and one or more disk-like, rotationally supported components which are typically young but can also be old.
This ‘two component model’ also explains the properties of our MW bulge. The MW is considered to have a boxy bulge, yet increased evidence of an old, α-enriched stellar population that formed on a short time-scale has resulted in a two component model (e.g. Tsujimoto & Bekki 2012). It has been shown that two stellar populations coexist in the Bulge separated in age and metallicity (McWilliam & Rich 1994, Feltzing & Gilmore 2000, van Loon et al. 2003, Groenewegen & Blommaert 2005, Zoccali et al. 2006, Fulbright et al. 2007, Zoccali et al. 2008) and that the separation extends somewhat to kinematics (Zhao et al. 1994, Soto et al. 2007), even if age determinations through color-magnitude diagram shows that most bulge stars in the Galaxy are older than 10 Gyr (Ortolani et al. 1995, Feltzing & Gilmore 2000, Zoccali et al. 2006, Clarkson et al. 2008).
The task of isolating the stellar population properties of the different subcomponents forming a bulge is difficult. Still, it has been tried by some authors. For example, Williams et al. (2011) study the stellar populations of two edge-on boxy/peanut shaped bulges. They place the slit along the major axis and observe with three offset in parallel positions. They found that NGC 1381 has a boxy bulge, with stellar rotation neither cylindrical (as would be expected for bars seen edge-on) nor strongly non-cylindrical and with a double hump on the rotation curve. The galaxy shows a metallicity gradient but no age gradient and a positive [α / Fe]. They explain the properties of these galaxies in an scenario where NGC 1381 has the three classes of bulges. The classical bulge formed their stars rapidly and explain the general trend in [α / Fe] as a function of height, as disk light (with its lower [α / Fe]) contributes less and less to the integrated spectrum. The boxy appearance is explained by the simultaneous presence of a bar (which appears boxy in projection), and the double hump of the rotation curve hints at the presence of a small disky pseudobulge (see also Sil’chenko et al. 2010).
1 Note, however, that a significant number of local massive spiral galaxies appears to have dominant pseudobulges, defined as those bulges with n < 2, that includes both disky and boxy/peanut bulges (Kormendy et al. 2010). Furthermore, pseudobulges are also found in S0 galaxies (Laurikainen et al. 2012). Back.
2 Classically, studies of stellar populations include E and S0 galaxies in the same group. Back.
3 Note, however, that the majority of low-luminosity elliptical galaxies are also rotationally supported (Emsellem & et al. 2011). Back.
4 The α elements are those chemical elements predominantly formed via fusion with a helium nucleus. Their most abundant isotopes therefore have nucleon numbers that are multiples of four (e.g., O, Ne, Mg, Si, S, Ar, Ca, Ti). These elements are mainly synthesized in Type II supernovae, while Type Ia supernovae produce elements of the iron peak (V, Cr, Mn, Fe, Co and Ni). In chemical evolution models, type II supernovae produce an early enrichment of α-elements followed by a subsequent enrichment of iron-peak, Type Ia supernovae products. In the absence of other modifying factors, this implies that [α / Fe] can be used as a ’galactic clock’ for the duration of the star formation. Back.
5 What it is usually measured is the Mg abundance through the Mgb index. Other α-elements, like Ca or Ti may follow different patterns (e.g. Conroy et al. 2014, Graves & Schiavon 2008, Cenarro et al. 2004). Back.
6 Note, however, that many of the exponential bulges were showing colors as red as the R1/4 bulges. Back.
7 Actually the author did not compare the index with stellar population models and, therefore, a variation in metallicity is also possible. Back.