

Two major advances in our understanding of the evolution of galaxies have occurred in the past five years or so. First, star forming galaxies (SFGs) are seen to be forming stars at a regular pace, forming the so-called main-sequence (MS; Brinchmann et al. 2004; Noeske et al. 2007; Daddi et al. 2007; Elbaz et al. 2007; Peng et al. 2010; Whitaker et al. 2012; Whitaker et al. 2014; Tomczak et al. 2016) an almost linear relation between star-formation rate (SFR) and stellar mass (M⋆). Second, star-forming galaxies have gas consumption time scales (defined as the time scale to consume the gas at the current SFR, i.e. Mgas/SFR) that are too short compared to the age of the Universe (at all epochs where gas masses can be measured, currently up to redshifts z = 2; Leroy et al. 2008; Genzel et al. 2010; Tacconi et al. 2013; Freundlich et al. 2013; Saintonge et al. 2013, 2016). Thus, in order to sustain the observed levels of star-formation over many Gyrs, galaxies must continuously replenish their gas reservoir with fresh gas accreted from the vast amounts available in the intergalactic medium.
Two additional indirect arguments point towards the necessity for gas accretion. One other argument comes from the metallicity distribution of sun-like stars (G-type) in the Milky Way, where the metallicity distribution of G-stars is not consistent with the expectation from chemical evolution models (whose initial condition is that of a pure gaseous reservoir, a.k.a. a ‘closed-box') unless some fresh gas infall is invoked (Lynden-Bell 1975; Pagel & Patchett 1975), a discrepancy often referred to as the G-dwarf problem (van den Bergh 1962; Schmidt 1963). Another another indirect argument for continuous replenishment of galaxy reservoirs comes from the non-evolving (or very weakly evolving) cosmic neutral density ΩHi for damped Lyα absorbers (Péroux et al. 2003; Bauermeiester et al. 2010; Noterdaeme et al. 2012; Zafar et al. 2013; Crighton et al. 2015) which contrasts with the rapid evolution of the stellar cosmic density.
In numerical simulations, accretion of intergalactic gas (via the cosmic web) originates from the growth of dark matter halos which pulls the cold baryons along. In galaxies with luminosities less than L*, this process is expected to be very efficient owing to the short cooling times in these halos (White & Frenk 1991; Birnboim & Dekel 2003; Kereš et al. 2005; Faucher-Giguère 2011). This phenomenon is often referred to as ‘cold accretion' and this term describes the halo mass regime (MDM < Mcrit) where the accretion is most efficient (White & Frenk 1991; Birnboim & Dekel 2003). At high masses and high redshifts, cold accretion can occur in the form of cold-streams (Dekel et al. 2009), i.e. when the halo is larger than the typical filament cross-section.
Once inside the galaxy dark matter halo, the accreted gas is expected to orbit the galaxy, the cold accreted gas should orbit about the halo before falling in to build the central disk, delivering not only fuel for star formation but also angular momentum to shape the outer parts of the galaxy (Stewart et al. 2011b; Shen et al. 2013; Danovich et al. 2015). Thus, accreting material should co-rotate with the central disk in the form of a warped, extended cold gaseous structure (Pichon et al. 2011; Kimm et al. 2011; Danovich et al. 2012, 2015; Shen et al. 2013), sometimes referred to as a “cold-flow disk” (Stewart et al. 2011a, 2013, 2016). This is further discussed in the chapter by K. Stewart.
In the local universe, such large gaseous disks are often seen around galaxies in Hi 21cm surveys, where the Hi disk extends 2–3 times beyond the stellar radius as in the M33 low surface brightness disk (Putman et al. 2009), the more massive M81 (Yun et al. 1994) and M83 galaxies (Huchtmeier & Bohnenstengel 1981; Bigiel et al. 2010), and others (see chapter by F. J. Lockman). The kinematics of this Hi gas in the outer parts show that the gas is systematically rotating in the same direction as the central object at those large radii (2–3 times beyond the stellar radius or 20-30 kpc).
As discussed in Stewart et al. (2011a), these gaseous disks (or “cold-flow disks”) should produce distinct kinematic signatures in absorption systems. In particular, the gas kinematics seen in absorption spectra are expected to be offset by about 100 km s−1 from the galaxy's systemic velocity. It should be noted that these cold-flow disks are the end product of cold accretion and these two terms should not be confused. Moreover, cold-flow disks occur on scales of a few tens of Rvir whereas cold accretion (or cold streams) occur on scales of Mpc, hence the possibility to observe with background quasars these two distinct phenomenon depends strongly on the gas column density. Theoretical expectations for detecting cold accretion with Lyman limit systems is discussed in Fumagalli et al. (2011); Goerdt et al. (2012) and in the chapter by C. A. Faucher-Giguère. Observational signatures of cold accretion with Lyman limit systems are discussed in the chapter by N. Lehner. This chapter focuses on the distinct absorption kinematics of “cold-flow disks” which should occur in the high column density regime and well inside the halos of galaxies.
Before discussing the most recent observations, it is important to
quantify how much accretion is needed in order to sustain the observed
levels of star-formation over many Gyrs to the levels of tens to
hundreds of solar masses per year at z = 1−2 required by
the main-sequence. This can be estimated from the following argument.
As shown in
Bouché et al. (2010)
and many others since
(Davé et al. 2012;
Krumholz et al. 2012;
Lilly et al. 2013;
Feldmann 2013,
Feldmann 2015;
Dekel & Mandelker 2014;
Forbes et al. 2014;
Peng & Maiolino 2014),
galaxies at z < 4 can be thought of as a simplified gas
regulator where there is a rough balance between the SFR and the gas
accretion rate. The equilibrium between gas accretion and SFR under the
‘regulator' model
(Lilly et al. 1963)
or ‘bathtub' scenario
(Bouché et al. 2010)
indicate that the accretion rate
 in should be
comparable to the star-formation rate (SFR).
in should be
comparable to the star-formation rate (SFR).
In particular, the equilibrium solution can be found from the continuity equation between the gas supply and gas consumption terms, and equilibrium SFR can be expressed as
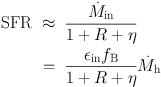 |
(1) |
where R is the gas returned fraction (from massive stars) under
the instantaneous recycling approximation, η the loading factor
from galactic winds, fB the universal baryonic
fraction and єin the efficiency of accretion (with
 in
≡ єin fB
in
≡ єin fB
 h) and
h) and
 h the dark
matter growth rate
(Genel et al. 2008;
McBride et al. 2009;
Dekel et al. 2013).
Equation 1 has several implications. First, it shows that SFR and the
accretion rate
h the dark
matter growth rate
(Genel et al. 2008;
McBride et al. 2009;
Dekel et al. 2013).
Equation 1 has several implications. First, it shows that SFR and the
accretion rate
 in are
comparable to a factor of order unity given that η is found to be
≈ 1
(Heckman et al. 2015;
Schroetter et al. 2015,
2016)
and that R ∼ 0.5 with its exact value depending on the
initial mass function.
Second, it shows that the evolution of the accretion rate
in are
comparable to a factor of order unity given that η is found to be
≈ 1
(Heckman et al. 2015;
Schroetter et al. 2015,
2016)
and that R ∼ 0.5 with its exact value depending on the
initial mass function.
Second, it shows that the evolution of the accretion rate
 in(z)
sets the evolution of the SFR
(Bouché et al. 2010).
Lastly, it is ultimately the dark matter growth rate that limits the
growth rate of galaxies and the evolution of SFR.
in(z)
sets the evolution of the SFR
(Bouché et al. 2010).
Lastly, it is ultimately the dark matter growth rate that limits the
growth rate of galaxies and the evolution of SFR.
Equation 1 is important because it shows that SFR is regulated by cosmological quantities (in other words it is supply-limited) and not necessarily the very local conditions (such as gas mass or gas surface density). The gas mass will adjust itself such that there is a close balance between SFR (consumption) and accretion (supply). However, as discussed in Bouché et al. (2010) and Lilly et al. (2013), beyond z > 4 or z > 6, the dark matter growth rate is so large that the SFR does not have the time to adjust itself towards the (quasi)-equilibrium solution, and thus this solution does not apply.