Over the last decade, an increasing number of theoretical studies have arrived at the conclusion that reasonably massive star-forming galaxies (M* > 1010 M⊙) grow in a quasi-smooth fashion whereby gas is accreted from the CGM and processed at roughly the same rate. This is a generalization of the idea that star formation self-regulates to match the gas accretion rate (Tinsley & Larson, 1978, Köppen & Edmunds, 1999) in that it replaces “star formation” with “gas processing”, where by the latter we mean that gas is processed either into stars or outflows. In this section, we introduce the concepts governing the equilibrium model and discuss inquiries into when and where it applies.
We begin by considering a galaxy to be a single zone
and define the growth rate of stellar mass in long-lived stars
*, the
rate of change of the gas mass
g, the gas
and star accretion rates
g,in,
*,in, and
the gas outflow rate
g,out.
Generically, these are related by
 |
(1) |
Equation 1 is a tolerably comprehensive statement of the conservation of baryonic mass within the context of galaxy evolution. Note that star formation does not appear in this equation because it does not change the galaxy's baryonic mass.
To derive the Equilibrium Model, we begin by assuming that accretion
of already-formed stars in actively star-forming galaxies is negligible;
that is,
*,in =
0. This implies that stellar mass growth owes predominantly to star
formation, or
* =
SFR, which is supported observationally
(Papovich et al.,
2011,
Behroozi et al.,
2013).
Next, we assume that the outflow rate equals the star formation rate of
long-lived stars multiplied by a slowly-varying “mass-loading
factor” η; that is,
g,out =
η
*.
Finally, we assume that
the galaxy balances accretion exactly with gas processing so that
g =
0. This condition cannot, of course, be exactly
correct, as it would imply that galaxies have no gas. However,
high-resolutions simulations suggest that, indeed, the mass of material
that is processed and ejected by disks is comparable to the mass that is
accreted
(Christensen et al.,
2016),
justifying it as a first-order approximation. What is left is
(Finlator et al.,
2008):
 |
(2) |
For clarity, we note that many authors define a total star formation rate
SFR, compute the “return fraction”, R, or the
fraction of mass that collapses into massive stars and is then returned
to the ISM on a short timescale
(Tinsley, 1980),
and then write down the growth of stellar
mass in long-lived stars as
* =
SFR(1 − R). In this case, we define η as the the ratio
of the outflow rate to the total star formation rate, and Equation 2 is
unchanged.
Equation 2 is a statement of gas processing equilibrium. The intuition is that, if the gas accretion rate temporarily exceeds the gas processing rate, then the gas density increases, boosting gas processing until the excess has been worked through. Conversely, if accretion temporarily sputters, then the gas density declines, choking off gas processing until new inflows are available. Equation 2 assumes that this balancing occurs on a timescale that is very short. In doing so, it departs conceptually from the traditional view that the star formation rate is fundamentally determined by the gas density. In an equilibrium scenario, the ISM adjusts itself so as to satisfy Equation 2; the gas density merely reflects the details of how it achieves this.
The factor of (1 + η) is what distinguishes Equation 2 from classical analytical models (Tinsley & Larson, 1978, Köppen & Edmunds, 1999). To see how important it is, consider the influences that determine a galaxy's gas-phase metallicity. At any given time, inflows from the CGM dilute the galaxy's metallicity. However, the inflows trigger continuing star formation, which simultaneously enriches the gas. The competition between dilution and enrichment gives rise to an Equilibrium Metallicity Zeq (Finlator et al., 2008, Davé et al., 2012):
 |
(3) |
Here, y is the metal yield, or the mass of metals ejected by core
collapse supernovae per mass of long-lived stars formed; and
Z0 is the metallicity
of inflowing gas, which for convenience we may re-cast as
Z0 ≡ αZ * Z, where
αZ is the ratio of the metallicity
of inflowing gas to the ISM metallicity and Z is the ISM
metallicity. If η is redefined such that η ≡ SFR /
g,out
where SFR is the total star formation rate, then we replace
η → η / (1−R) in Equation 3. Note that
we assume that outflows have the same metallicity as the ISM; this is
supported by high-resolution simulations (for example, Figure 11 of
Ma et al. (2016).
Equation 3 is a statement of enrichment equilibrium. The
intuition is that enrichment and dilution balance each other once the
galaxy's metallicity reaches Zeq. If Z somehow
jumps above Zeq, then inflows dilute it. If Z
dips, then continued
star formation boosts it back to Zeq. If the SFR responds
instantaneously to fluctuations in the inflow rate, then departures
from Zeq are erased on a dilution time
Mg /
g,in, or
the timescale for inflows to replenish the ISM completely.
Equations 2–3 involve two parameters, η and Z0. For galaxies that are massive enough to be in equilibrium, the slope and redshift-dependence of the mass-metallicity relation may be expressed as evolution in these parameters.
In order to illustrate how powerful Equation 3 is, we use it to interpret the z = 0 mass-metallicity relation (where by “metallicity” we mean the oxygen mass fraction Zox). In each panel of Figure 1, the black dashed line indicates Z under the assumption of pristine inflows (Z0 = 0), an oxygen yield of y = 0.01, and no outflows (η = 0). Meanwhile, the blue dotted curve is the observed trend at z ∼ 0.1 (Andrews & Martini, 2013), where we convert from units of 12 + log(O/H) to oxygen mass fraction assuming a hydrogen mass fraction of 0.76.
 |
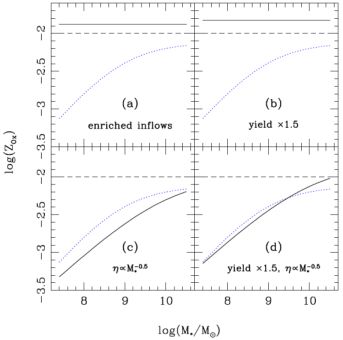Figure 1. Illustration of the parameters that control metallicity in Equation 3. In each panel, the black dashed line indicates the same “base model” while the blue dashed curve is the observed trend (Andrews & Martini, 2013). The bottom-right panel shows that Equation 3 can be tuned to achieve good agreement with observations. |
With no outflows (η=0), metallicity has no dependence on mass as shown by the dashed black segment in each panel of Figure 1. Increasing the inflow metallicity Z0 from 0 to 0.00333 boosts Z at all masses (panel a). Likewise, increasing the yield y from 0.01 to 0.015 increases Z at all masses (panel b). Assuming that the outflow rate η varies with stellar mass as (1010 M⊙ / M*)0.5 immediately yields a strong dependence of Z on M* (panel c). Finally, restoring the assumption of pristine inflows and tuning both the yield and the outflows yields a plausible level of agreement with observations (panel d). We do not use a rigorous approach to tune our parameters because our goal is merely to illustrate its potential as a conceptual framework. However, the model has been generalized and tuned elsewhere, yielding promising insight into the nature of the baryon cycle (Mitra et al., 2015, Mitra et al., 2016); we will discuss these efforts shortly.
This exercise shows that the MZR can easily be interpreted within the equilibrium scenario (Equations 2–3). However, the interpretation's value is limited by model's simplicity. For example, η and Z0 could vary with redshift, and Z0 could additionally vary with mass. For improved realism, further insight from numerical models is required.
η is now relatively well-studied theoretically, with a consensus that it decreases with increasing mass and exceeds 1 in halos whose circular velocity vcirc lies below 60 km s−1 (Muratov et al., 2015, Christensen et al., 2016). In detail, there is an ongoing debate as to whether it follows expectations from momentum-driven or energy-driven outflows. Briefly, if the characteristic speed of galactic outflows is the halo circular velocity vcirc and if star formation deposits a constant amount of energy in outflows per unit of stellar mass formed, then η varies as vcirc−2. Alternatively, if star formation deposits a constant amount of momentum in outflows per unit of stellar mass formed, then η∝ vcirc−1 (Murray et al., 2005).
We show three recent estimates for η in Figure 2. Muratov et al. (2015) use high-resolution numerical simulations to find that vcirc−1.0 for vcirc > 60 km s−1 and vcirc−3.2 at lower masses. By contrast, Christensen et al. (2016) study a complementary suite of high-resolution simulations and derive η ∝ vcirc−2.2 at all masses. These simulations model star formation and feedback in different ways, hence it is telling that they both predict η > 1 for vcirc < 60 km s−1 and η > 4 for vcirc = 30 km s−1, which is the lowest halo mass that can efficiently accrete baryons from a photoheated IGM (Gnedin, 2000, Okamoto et al., 2008). The generally higher values of η found by Muratov et al. (2015) probably reflect additional feedback sources such as radiation pressure that are not considered in the Christensen et al. (2016) model.
 |
Figure 2. Recent models for the ratio η of the gas outflow rate to the star formation rate (a.k.a. the mass-loading factor). The models of Christensen et al. 2016 and Muratov et al. 2015 are high-resolution ab-initio simulations. The Mitra et al. 2015 curve results from fitting an equilibrium model to observations. The momentum-driven and energy-driven scalings are arbitrarily normalized to η = 1 at 60 km s−1. |
Mitra et al. (2015) take a different approach and use a Bayesian Monte Carlo Markov Chain approach to infer η (among other things) directly from observations. In particular, they assume that galaxies obey Equations 2–3 at all times and then infer the parameters that are required in order to match simultaneously the observed stellar mass - halo mass relation, the MZR, and the stellar mass - star formation rate relation. They find that η ∝ Mh−1.16∝ vcirc−3.48, slightly steeper than the dependencies obtained from numerical simulations. When η is expressed as a function of stellar mass, however, the differences shrink: Muratov et al. (2015) find η∝ M*−0.35 while Mitra et al. (2015) find η ∝ M*−0.5 for M* < 1010 M⊙ (note that this is the same scaling as in panel d of Figure 1).
Given that η decreases with mass both in ab-initio calculations and in efforts to model observations, it assuredly drives the MZR's slope: As shown in Figure 1, a large η removes more enriched gas, with the result that dilution by inflows is more efficient at suppressing the gas metallicity. This in turn leads to a positive dependence of Z on mass.
The way in which enriched inflows (that is, Z0 > 0) affect the MZR has received considerably less study than η but is probably just as important. Davé et al. (2011) showed that, on average, αZ increases with time, driving or at least contributing to the observed growth in the MZR's normalization. The analysis of metal flows in high-resolution simulations presented by Ma et al. (2016) qualitatively supports this view. Furthermore, it suggests that inflows into massive halos (those that grow to 1011 M⊙ by z = 0) have roughly one third the ISM's metallicity at all times, or αZ ∼ 1/3. Meanwhile, the αZ in low-mass halos (1010 M⊙ at z = 0) falls from ∼1/3 at early times to a few percent at z = 0.
In short, both η and Z0 probably vary in a way that drives an MZR to increase with mass and time. The connection between this differential dilution and the MZR depends critically on the equilibrium model. This discussion then raises several points for future research.
Which galaxies are in equilibrium? As discussed in Section 3, observations suggest that low-mass halos depart from equilibrium expectations in the sense that they do not cool their gas onto galaxies at the same rate as they accrete it from the IGM. Is there a similar mass cutoff below which galaxies do not convert their stars into gas at the same rate as they accrete it from the CGM? Does it vary with redshift? If so, then one expects the MZR normalization to plummet above the redshift at which galaxies first achieved equilibrium. Indeed, observations have suggested that the MZR drops rapidly in normalization from z = 2–3 (Maiolino et al., 2008) and then flattens (that is, the mass dependence weakens) to z = 5 (Faist et al., 2016). This behavior could indicate that z ≥ 3 is the “gas accumulation” epoch, when metal and dust production were swamped by inflows and η and αZ did not yet govern metallicities. A detailed analysis of what is expected from hydrodynamic simulations in this regard would be illuminating.
What is equilibrium?
For completeness, we note that, while some works define gas processing
equilibrium as the condition that a galaxy's gas mass be constant
Finlator et
al. (2008),
Davé et
al. (2011),
Davé et
al. (2012),
it may be equally defensible to propose
that a galaxy's gas fraction [defined as µ ≡
Mg / M* or Mg /
(Mg + M*)] is constant
(Feldmann, 2013).
If true, then the equilibrium metallicity is
slightly different from Equation 3 (i.e., set
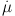≡ 0
in Equation 4). It would be interesting to ask which of
these conditions more accurately describes galaxy growth in cosmological
simulations or semi-analytical models.
Can we close the loop? Once the mass and redshift range has been identified where galaxies are expected to be in equilibrium, it would be interesting to ask whether Equations 2–3 really do govern the observed evolution within simulations and models. Conceptually, this would be accomplished in several (rather involved) steps:
= 0;
A more complete conceptual understanding of what governs the MZR in hydrodynamic simulations or semi-analytical models would inform the interpretation of existing and upcoming observations.
If the equilibrium model describes galaxies as a whole, then it is natural to ask whether it also describes individual regions within the galaxy. There is a lower limit of course; we would not apply the equilibrium model on spatial scales comparable to a molecular cloud (10–100 pc) where metals diffuse or are spread by individual supernovae. But what about a region of characteristic size ∼1 kpc? To be specific, we may ask two questions:
Within the context of an analytical model, Fu et al. (2013) found that radial flows do not impact the overall metallicity gradient while inflows do. They did not study the extent to which individual annuli were in equilibrium, and the assumptions that were necessarily to make their model tractable were strong, motivating further insight from numerical models.
A year later, a different group took the bait and carried out a detailed study of high-resolution, one-dimensional simulations of star-forming disks (Forbes et al., 2014a). They found that, indeed, individual annuli do obey Equation 2 locally. In detail, the way in which cosmological inflows, star formation, galactic outflows, and radial gas flows (triggered by gravitational instability-driven torques that occur wherever gas densities are high) balance varies with mass and with redshift. Annuli at large radii have low densities and low star formation rates, hence they do not efficiently process newly-accreted gas or transport it to smaller radii. Moving inwards, gas densities increase to the point that star formation and radial transport of gas balance accretion. Near a galaxy's center, star formation and outflows are so efficient that they can only be balanced by radial transport of gas from larger radii; cosmological inflows are a subdominant gas source here. The slowly-declining cosmological infall rate causes this balance to evolve in such a way that the region where gas is gravitationally unstable migrates outwards with time. By z = 0 it operates only in galaxies' outskirts, if at all.
The finding that high-redshift galaxies obey Equation 2 locally as well as globally certainly raises the hope that Equation 3 also applies, but Forbes et al. (2014a) unfortunately do not comment on the predicted metallicity gradients or their evolution. However, simple applications of this idea have been able to accommodate locally-observed radial trends fairly well (Carton et al., 2015).
It would be interesting to compare high-resolution one-dimensional simulations (Forbes et al., 2014a) with lower-resolution cosmological simulations (Pilkington et al., 2012) in order to assess (1) Whether cosmological simulations resolve gravitational instabilities and their impact; (2) Whether there are effects in three-dimensional simulations (such as bars) that modulate gas flows and that cannot be captured in one-dimensional simulations; and most broadly (3) Whether the cosmological simulations predict the same level of equilibrium as the one-dimensional simulations. Likewise, it would be useful to distill insights from the Forbes et al. (2014a) study (such as the the radial flow rate) into a form that can be used to improve the realism of semi-analytical models.
We conclude from these studies that the expected signature of cosmological inflows in galaxies' metallicity gradients remains unclear theoretically. There is room both for an improved understanding of observed metallicity gradients (Section 2.2), and of what they are telling us about inflows and gas processing.