


Observations indicate that there is more to galaxy metallicities than equilibrium. For example, at a fixed stellar mass, galaxies show finite scatter in gas-phase metallicity (Tremonti et al., 2004, Zahid et al., 2012, Guo et al., 2016), and in star formation rate (Whitaker et al., 2012). Do these observations reflect intrinsic scatter in η or Z0, or do they indicate departures from equilibrium?
The observed level of scatter is intuitively consistent with the idea that star formation is at least slightly irregular or “bursty” at any mass, which could be associated with departures from equilibrium. For example, if star formation rate is driven by stochastic processes (Gerola et al., 1980) or if the ISM responds slowly to inflow fluctuations, then the galaxy would not be perfectly in equilibrium (Forbes et al., 2014b); this is in fact expected for dwarf galaxies (Lilly et al., 2013, Hopkins et al., 2014, Wise et al., 2014). Alternatively, the burstiness could owe to irregular inflows, which are not themselves completely smooth. Indeed, it has been shown that, by modeling the bursty inflow rates realistically but retaining the assumption that galaxies are in perfect equilibrium with those bursty inflows (which is theoretically supported Rathaus & Sternberg (2016)), the observed level of scatter can be accounted for (Mitra et al., 2016, Dutton et al., 2010). This means that the observed scatter need not reflect truly out-of-equilibrium behavior.
The most important handle on the nature of the observed scatter is the identification of correlated departures from equilibrium, in particular departures from mean-trend behavior in Z, SFR, and gas fraction at constant M*, as quantified by mean scaling relations. These have prompted a range of generalizations to the Equilibrium Model. Before delving into the models, however, we review the observations.
5.1. The M*-Z-SFR Relation: Observations and Intuition
Ellison et al. (2008) first pointed out that the SDSS MZR has a third-parameter dependence on SFR in the sense that, at a fixed M*, galaxies with higher SFR have lower Z. Subsequently, other authors have found qualitatively similar results at a variety of redshifts (Mannucci et al., 2010, Lara-López et al., 2010, Cresci et al., 2012, Hunt et al., 2012, Henry et al., 2013, Stott et al., 2013, Cullen et al., 2014, Maier et al., 2014, Nakajima & Ouchi, 2014, de los Reyes et al., 2015, Salim et al., 2015, Kacprzak et al., 2016). There have been suggestions that the SFR-dependence reflects observational systematics or disappears at high redshift (Sánchez et al., 2013, Steidel et al., 2014, Sanders et al., 2015). However, detailed analyses of possible biases have shown that it persists even if a variety of effects is taken into account both in the SDSS sample (Andrews & Martini, 2013, Salim et al., 2014, Telford et al., 2016) and at high redshift (Salim et al., 2015). Moreover, early suggestions that the sign of the effect has a mass dependence in the sense that massive galaxies with enhanced SFR have enhanced metallicity (Yates et al., 2012) may simply reflect tricky selection biases (Salim et al., 2014, Salim et al., 2015). Initial results suggesting that the M*-Z-SFR relation is redshift-independent gave rise to the idea that the M*-Z-SFR relation is “fundamental” (Mannucci et al., 2010), which would be powerful if true. However, more recent results indicate that, while the sense of the SFR dependence is unchanged throughout z = 0–2.3, its strength evolves (Brown et al., 2016, Grasshorn Gebhardt et al., 2016), particularly at high stellar masses (1011 M⊙; Salim et al. (2015)).
While the dependence of metallicity on SFR was identified first, it has recently been argued that the dependence on gas fraction is just as strong, if not stronger (Hughes et al., 2013, Bothwell et al., 2013, Lara-López et al., 2013, Bothwell et al., 2016). This result has also been found in cosmological simulations (Lagos et al., 2016). These findings indicate that SFR perturbations really just serve as a proxy for gas supply perturbations. In other words, the M*-Z-SFR relation is driven by bursty inflows rather than bursty star formation (Dutton et al., 2010, Mitra et al., 2016). SFR is much easier to measure for large samples, however, and will probably continue to be used as the de facto third parameter for some time.
It thus appears that the M*-Z-SFR relation is real, if perhaps a bit elusive. Theoretical explanations generally invoke a picture along the following lines: suppose that a galaxy is growing in a quiescent way that obeys Equations 2–3. If, for some reason, the gas accretion rate increases, two things will happen. First, the gas mass will grow, likely suppressing the galaxy's metallicity. Second, the SFR will increase owing to the boosted gas density. Finally, the perturbations to Z and SFR subside once the extra gas is processed and the metallicity is diluted by further inflows (Dalcanton, 2007).
Of course, one could also imagine the opposite effect: Dips in the gas accretion rate could lead to suppressed SFR and enhanced metallicity (because the metals generated by ongoing star formation would be less diluted by inflows). The problem with this is that, whereas accretion spikes can increase the size of the gas reservoir and boost SFR on a disk dynamical time (∼100 Myr), accretion dips can only suppress the SFR on the timescale given by the gas mass divided by the SFR. This is, to within a factor of a few, the same as the halo specific growth rate, or 1–10 Gyr (see, for example, Figure 3 of Lilly et al. (2013)). It is perhaps for this reason that, observationally, the M*-Z-SFR dependence is driven by systems with enhanced SFR (Salim et al., 2014, Telford et al., 2016), and evidence for short-term accretion dips is hard to come by.
A variety of theoretical approaches have been used to study the scatter in the M*-Z-SFR relation and its possible use as a probe of gas inflows. We now summarize key insights gleaned from these efforts.
5.2. The M*-Z-SFR Relation: Equilibrium Treatments
5.2.1. The Power of Assuming
 =
=
 g =
0: Davé et al. 2012
g =
0: Davé et al. 2012
Inspired by cosmological hydrodynamic simulations, Davé et al. (2012) devised an equilibrium model that relates galaxy growth to host halo growth under the condition that galaxies obey Equations 2–3. In order to connect halo growth with galaxy growth, they parameterized the impact of photoionization heating, quenching by accretion shocks, and re-accretion of previously ejected gas. They also studied the condition for galaxies to be in gas processing equilibrium, finding that there is a characteristic redshift above which galaxies cannot process their gas as rapidly as they accrete it. The precise redshift depends both on halo mass and on the outflow model because stronger outflows lead galaxies to reach equilibrium sooner. For momentum-driven outflow scalings, 1012 M⊙ halos achieve equilibrium at z ∼ 5 while galaxies in lower-mass halos (≤ 1011 M⊙) are always in equilibrium (because their outflows are strong). Hence star-forming galaxies are in or near equilibrium for most of cosmic time.
Equations 2–3 are too simple to permit a
third-parameter dependence of Z on SFR, but
Davé et
al. (2012)
did note that such a dependence arises naturally in hydrodynamic
simulations and can readily be attributed to weak violations of the
condition
 g = 0.
g = 0.
The Davé et al. (2012) picture has since been generalized into an eight-parameter model and tuned to match the observed relationships between M*, Z, SFR, and halo mass as well as their redshift dependence and scatter (Mitra et al., 2015, Mitra et al., 2016). The resulting fits are excellent, supporting the model's realism. Notably, three of the eight parameters describe the rate at which ejected gas re-accretes and two describe “quenching”, or the suppression of inflows into galaxies hosted by massive halos. Such quenching could be associated, for example, with active galactic nuclei or virial shocks. These studies show forcefully that, within a suitable framework, it is possible to use observations of Z and SFR to constrain the efficiency of inflows.
5.2.2. Relaxing Gas Processing Equilibrium: Lilly et al. 2013
Initial efforts to interpret ensemble measures of galaxy evolution within an equilibrium framework assumed that the galaxy's gas reservoir does not grow (Finlator et al., 2008, Davé et al., 2011, Davé et al., 2012). However, it was soon realized that relaxing this assumption and allowing the gas fraction to fluctuate naturally gives rise to a M*-Z-SFR relation that qualitatively resembles observations (Lilly et al., 2013). Re-deriving the condition for enrichment equilibrium while relaxing the assumption of gas processing equilibrium leads to a generalization of Equation 3:
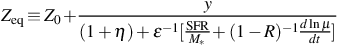 |
(4) |
Here, є−1 is the star formation timescale and µ ≡ Mg / M* is the ratio of gas mass to stellar mass. Equation 4 beautifully connects Z, SFR, and M*. If the timescale є−1 for a galaxy to run through its gas reservoir is very short, then Z should not correlate with SFR because the ISM recovers quickly from perturbations (by processing gas efficiently). In this case, the gas mass is constant and Equation 4 reduces to Equation 3. On the other hand, if star formation is less efficient (є−1 is longer), then the ISM can be out of gas processing equilibrium for some time. In this case, a high specific star formation rate SFR / M* is associated with a low metallicity as observed, irrespective of the relationship between the inflow and gas processing rates.
After presenting this model, Lilly et al. (2013) used it to draw a number of inferences from observations. In particular:
The gas regulator model contains a number of approximations, chief among them the assumption of enrichment equilibrium. It is naturally of interest to ask whether the model describes what happens within a less approximate framework. Pipino et al. (2014) tested the Lilly et al. (2013) model using exact analytical expressions for the evolution of gas-phase metallicity, gas mass, and star formation rate, finding excellent agreement across a wide range of potential growth histories. This suggests that the gas regulator model is a powerful generalization of the equilibrium model introduced by Davé et al. (2012). Not surprisingly, it is now being tested and applied in a wide variety of contexts (for example, Birrer et al. (2014), Dekel & Mandelker (2014), Bouché & Blandin (2015), Wu et al. (2016)).
To date, there has been no effort to determine whether the Lilly et al. (2013) model describes what happens within three-dimensional hydrodynamic simulations or semi-analytical models; this may be a promising avenue for future research.
5.3. The M*-Z-SFR Relation: Non-equilibrium Treatments
5.3.1. An Analytical Model Without Equilibrium: Dayal et al. 2013
Can the observed M*-Z-SFR relation can be explained without any explicit assumption of equilibrium? In a purely analytical study, Dayal et al. (2013) presented a minimal model for galaxy growth in which the evolution of the stellar, gas, and metal reservoirs depends only on the unknown gas accretion and outflow rates. They assume that outflow and infall rates depend only on stellar mass, that the metal yield y is constant, and that inflows are pristine. They then show that they can fit the model's governing parameters using the the observed M*-Z-SFR relation (Mannucci et al., 2010) to achieve good agreement.
In common with Lilly et al. (2013), this model predicts no evolution in the overall M*-Z-SFR relation for a given set of parameters, but it has the advantage that it assumes neither gas processing or enrichment equilibrium. Nonetheless, a mass-dependent balance between inflows and outflows emerges as a a central prediction. Massive galaxies have weak winds and rapidly achieve enrichment equilibrium (similar to Equation 3, although they do not impose this). By contrast, low-mass galaxies lose most of their metals through much stronger outflows and are hence more susceptible to dilution.
In fact, they show that, subject to their modeling assumptions, the infall rate and its mass dependence can be inferred directly from the observed M*-Z-SFR relation. Intriguingly, the inferred outflow rate η varies with mass in a way that follows expectations from momentum-driven outflow models (Murray et al., 2005). The model can also accommodate high-redshift observations, with the result that gas fractions and inflow rates were previously higher while outflow efficiencies were essentially the same (Hunt et al., 2016).
Their model also naturally reproduces the observed relation between oxygen abundance and neutral gas fraction (Hughes et al., 2013). This finding reinforces the tight connection between metallicity and gas fraction that emerges in any plausible model of galaxy growth. It would be interesting to ask whether re-writing the Dayal et al. (2013) model to match the observed M*-SFR-gas fraction relation automatically recovers the Z dependence. Likewise, it would be interesting to quantify precisely how close the galaxies are to enrichment and gas processing equilibrium in the Dayal et al. (2013) model once the inflow and outflow parameters are tuned to match observations.
5.3.2. Stochastic Accretion Histories and Scatter: Forbes et al. 2014
Observationally, there is residual scatter in Z even after the SFR dependence is removed (Salim et al., 2014, Salim et al., 2015). Can this scatter be used as a complementary probe of inflows and gas processing? This question is taken up by Forbes et al. (2014b), who propose that, even if individual galaxies are not in equilibrium, they may be close enough to it that ensemble statistics such as the slope of the Z-SFR relation are in equilibrium. They explore this idea by modeling galaxy growth as a connected sequence of intervals whose constant duration is given by the “coherence time” tcoherence. At the start of each interval, a new accretion rate is drawn from a log-normal distribution with fixed median and scatter. The galaxy then uses star formation and outflows to respond to the new accretion rate on a “loss timescale” tloss, which incorporates gas losses to both outflows and star formation. If tloss is short compared to other timescales, then galaxies are always in equilibrium. Conversely, if tloss is long, then they retain a “memory” of previous accretion episodes.
The model's parameters can be tuned to yield qualitative agreement with the observed M*-Z-SFR relations. This has two important implications:
The price for relaxing the assumption of equilibrium is that this model is more complicated than the Lilly et al. (2013) or Davé et al. (2012) models. It would therefore be useful to ask how close galaxies are to equilibrium when this model is tuned to reproduce observations. Moreover, as the authors point out, the Forbes et al. (2014b) model for inflow fluctuations is extremely simple, invoking only a single coherence timescale. In reality, inflows fluctuate on a range of timescales. It would therefore be useful to generalize this aspect of the model for improved realism.
5.3.3. Cosmological Hydrodynamic Simulations
Cosmological hydrodynamic simulations and semi-analytical models make fewer assumptions regarding inflows and gas processing than analytical models (Somerville & Davé, 2015), and are hence a particularly realistic framework for studying the M*-Z-SFR relation. Reassuringly, they inevitably predict relations that qualitatively resemble observations (Davé et al., 2011, Yates et al., 2012, Obreja et al., 2014, de Rossi et al., 2015, Kacprzak et al., 2016, Lagos et al., 2016, Cousin et al., 2016).
In order to understand this prediction better, Lagos et al. (2016) apply a principal component analysis to the predicted ensemble distribution of global galaxy attributes in the Eagle simulations (Schaye et al., 2015). In agreement with previous work, they identify a particularly thin plane in the space of M*, SFR, and neutral+molecular gas fraction where simulated galaxies tend to live. Moreover, they show that this plane is observed. They interpret its existence as an indication that galaxies live in a slowly-evolving balance between gas accretion and gas processing reminiscent of Equation 2. Interestingly, the predicted scatter about this plane tightens if stellar feedback assumed in the model is stronger. This could readily reflect the fact that fresh inflows drive galaxies back to their equilibrium state more quickly if the gas fraction is lower.
Just as the statistics of the EAGLE galaxies imply a balance between gas inflows and processing, they also imply a balance between dilution and enrichment: the predicted metallicity is correlated with the gas fraction in the observed sense, namely that galaxies with high gas fractions have systematically low metallicities. Interestingly, however, it is found that Z contributes less to the overall variation in galaxy properties than M*, SFR, and gas fraction: whereas the latter three attributes dominate the first principal component, Z only enters into the second. This qualitatively supports observational suggestions that gas fraction is more fundamental than metallicity (Hughes et al., 2013, Bothwell et al., 2013, Lara-López et al., 2013, Bothwell et al., 2016). Further theoretical work is needed in order to understand why gas fraction is more fundamental.
Unlike recent high-resolution simulations of individual galaxies (Christensen et al., 2016, Ma et al., 2016), the study presented in Lagos et al. (2016) stops short of directly measuring the flow of gas and metals through the simulated galaxies because it is based on a principal-component analysis, which leverages the statistical advantage that lower-resolution cosmological simulations have over high-resolution “zoom” studies. This means that they do not ask whether galaxies keep gas mass or gas fraction constant, or how Z0 varies with mass and redshift. It would therefore be interesting to merge the two approaches by quantifying the expected flow of gas and metals in cosmological simulations in order to understand in more detail how they give rise to the M*-Z-SFR-gas fraction relation.
5.3.4. An Analytical Model Without Inflows: Magrini et al. 2012
Thus far, all of the models for the M*-Z-SFR relation that we have discussed invoke inflows, giving the impression that cosmological inflows of pristine gas are an unavoidable inference. A different perspective is offered by Magrini et al. (2012), who construct analytic, one-zone, closed-box evolutionary models that qualitatively match the observed M*-Z-SFR relation. The key ingredient in their model is a distinction between “active” and “passive” modes of star formation: active-mode galaxies have high-density molecular clouds whose collisions trigger vigorous star formation while the clouds in passive-mode galaxies are more diffuse. When they confront their model with observations, they find that most high-redshift galaxies and the occasional, unusually active low-redshift ones can be identified with the active mode while quiescent systems can be identified with the passive mode.
While it is interesting that the model in Magrini et al. (2012) contains observations within its accessible parameter space, the discussion leaves several basic questions unaddressed. First, the model does not predict the distribution of active and passive-mode systems or its evolution. Hydrodynamic simulations attribute the prevalence of active-mode star-formers at high redshift and the scaling relations that they obey to high gas accretion rates and the detailed way in which galaxies achieve an equilibrium with those inflows (Forbes et al., 2014a, Lagos et al., 2016). By contrast (and similarly to Dayal et al. (2013)), Magrini et al. (2012) attribute the observed scaling relationships to unexplained variations in initial conditions, evolutionary state, and ISM properties. Second, the lack of inflows means that the Magrini et al. (2012) predicts stellar metallicity distributions that conflict with local observations (Section 1). Future work that includes inflows following cosmological expectations may reconcile this model with simulations.