Annu. Rev. Astron. Astrophys. 2015. 53:115-154 Copyright © 2015 by Annual Reviews. All rights reserved

4. THE WIND SHOCK

So far we have only studied the black hole wind. But we know that this wind must have a significant effect on the host galaxy when it impacts directly on its interstellar medium (ISM). In this Section we model the wind and host ISM as roughly spherically symmetric, and consider the effects of deviations from this simple picture later.

The pattern of the wind–ISM interaction (Figure 7) is qualitatively identical to that of a stellar wind hitting the interstellar medium around it (see e.g. Dyson & Williams 1997). The black hole wind (shown in blue) is abruptly slowed in an inner (reverse) shock where the temperature approaches ∼ 10¹¹ K if ions and electrons reach equipartition (but see the discussion below). The shocked wind gas acts like a piston, sweeping up the host ISM (shown in red) at a contact discontinuity moving ahead of it. Because this swept–up gas moves supersonically into the ambient ISM, it drives an outer (forward) shock into it (see Figs. 7 and 8 [top]).

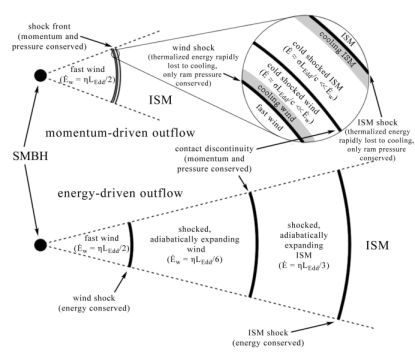Figure 8. Schematic picture of momentum–driven (top) and energy–driven (bottom) outflows. In both cases a fast wind (velocity ∼ 0.1c) impacts the interstellar gas of the host galaxy, producing an inner reverse shock slowing the wind, and an outer forward shock accelerating the swept–up gas. In the momentum–driven case (top), corresponding to the UFOs discussed in Section 2, the shocks are very narrow and rapidly cool to become effectively isothermal. Only the ram pressure is communicated to the outflow, leading to very low kinetic energy ∼ (σ / c)LEdd. In an energy–driven outflow (bottom), the shocked regions are much wider and do not cool. They expand adiabatically, communicating most of the kinetic energy of the wind to the outflow (in simple cases divided in a ratio of about 1:2 between the shocked wind and the swept–up gas). The outflow radial momentum flux is therefore greater than that of the wind. Momentum–driven conditions hold for shocks confined to within ∼ 1 kpc of the AGN, and establish the M − σ relation (42) (King, 2003; King, 2005). Once the supermassive black hole mass attains the critical M − σ value, the shocks move further from the AGN and the outflow becomes energy–driven. This produces the observed large–scale molecular outflows which probably sweep the galaxy clear of gas. (From Zubovas & King, 2012a).

The dominant interaction here is the reverse shock slowing the black hole wind, and injecting energy into the host ISM. The nature of this shock differs sharply depending on whether or not some form of cooling (typically radiation) removes significant energy from the hot shocked gas on a timescale shorter than its flow time. If the cooling is strong in this sense (‘momentum–driven flow’), most of the preshock kinetic energy is lost (usually to radiation). The very rapid cooling means that the shocked wind gas is highly compressed, making the postshock region geometrically narrow (see the upper part of Figure 8). This kind of narrow, strongly cooling region ia often idealised as a discontinuity, know as an ‘isothermal shock’ (cf Dyson & Williams, 1997). As momentum must be conserved, the postshock gas transmits just its ram pressure (21) to the host ISM. We will see that this amounts to transfer of only a fraction ∼ σ / c ∼ 10⁻³ of the mechanical luminosity E_{BH wind} ≃ 0.05L_Edd (cf equation 23) to the ISM. In other words, in the momentum–driven limit, only energy

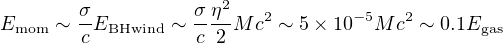(31)

is injected into the bulge ISM, i.e. about 10% of the bulge gas binding energy f_g M_bσ² for black holes close to the M − σ relation (there is now an implicit factor σ₂₀₀⁵ / M₈ on the rhs). Thus momentum–driven flows do not threaten the bulge's integrity. Indeed we will see that they never interact with most of it, so there is no danger that the black hole will drive away the gas and suppress accretion. A momentum–driven regime is a stable environment for black–hole mass growth.

In the opposite limit where cooling is negligible, the postshock gas retains all the mechanical luminosity

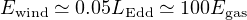(32)

(cf equation 24) thermalized in the shock, and instead expands adiabatically into the ISM. The postshock gas is now geometrically extended (see the lower part of Figure 8), unlike the momentum–driven (‘isothermal’) case. This ‘energy–driven flow’ is much more violent than momentum–driven flow. The estimate (32) is for a black–hole mass near the M − σ relation; a hole with mass a factor of 100 below this would already unbind the bulge in doubling its mass. Unless the shock interaction is markedly aspherical, a black hole in an energy–driven environment is unlikely to reach observed SMBH masses.

Given these starkly different outcomes we must decide under what conditions we have momentum– or energy–driven outflows. Simple estimates immediately show that ordinary atomic two–body processes have no significant effect in cooling the wind shock. But the wind shock is exposed to the radiation field of an Eddington–accreting supermassive black hole. This has a characteristic temperature of no more than ∼ 10⁷ K, far lower than the wind's immediate post-shock temperature of ∼ 10¹⁰ − 10¹¹ K. Electrons in the postshock gas lose energy to these photons through the inverse Compton effect (cf Ciotti & Ostriker, 1997), at a rate dependent on the radiation density. For wind shocks close to the SMBH, the accretion radiation field is intense enough that this effect cools the postshock wind gas in less than the momentum–driven flow time ∼ R/σ (see below), and we are self–consistently in the momentum–driven regime, provided that the postshock gas is in equipartition, i.e. that electron and ion temperatures remain effectively equal. (We consider this further in Section 4.2 below.)

For shocks at larger radii R the radiation energy density decreases as R⁻², increasing the cooling time as R². The flow time increases only as R, so for R greater than the critical cooling radius

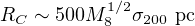(33)

(King, 2003, 2005; King et al. 2011, Zubovas & King 2012b) the cooling time is longer than the flow time, and the flow must be energy–driven. So we have the general result that momentum–driven flows are confined to a small region R < R_C, while energy–driven flows must be large–scale. This is just as one would expect, given that a momentum–driven flow allows stable black hole mass growth, while an energy–driven one is likely to expel most of the bulge gas.

It is plausible then that the observed UFO winds can lead to momentum–driving through strongly cooled shocks close to the SMBH. In this picture all but a small fraction of the mechanical luminosity (23) of the black hole wind is eventually radiated away as an inverse Compton continuum with characteristic photon energy ∼ 1 keV. Pounds & Vaughan (2011) report a possible detection of this spectral component in the Seyfert 1 galaxy NGC 4051. As required for consistency, the luminosity of this component is comparable to the expected mechanical luminosity (23) of the wind in that system.

Cooling shocks are called ‘isothermal’ because the gas temperature rapidly returns to something like its preshock value. Momentum conservation requires that the gas is also strongly slowed and compressed as it cools. So the postshock velocity of the X–ray emitting gas should correlate with its temperature (or roughly, ionization) while Compton cooling is dominant. Once this has compressed the gas sufficiently, two–body processes such as free–free and bound–free emission must begin to dominate, since they go as the square of the density, and their cooling times decrease with temperature also (Pounds & King 2013). Section 2.5 above shows that there is direct observational evidence for both of these effects in NGC 4051. So this object (uniquely) shows three signatures of a cooling shock: an inverse Compton continuum, an ionization–velocity correlation, and the appearance of two–body processes in the spectrum.

4.2. Shock Cooling

Cooling (or the lack of it) has a defining effect on the physics of the interaction between the black hole wind and the host ISM, so we must check the simple picture above. In particular the inverse Compton effect acts only on electrons, but the energy of the postshock gas is initially almost all in its ions. We assumed above that the electron and ion temperatures quickly come into equipartition after the shock, allowing the inverse Compton effect to drain energy from the ions.

This assumption can be questioned. Faucher-Giguère & Quataert (2012) show that if the only process coupling electrons and ions is Coulomb collisions, there is a significant parameter space where equipartition does not occur, although they do not rule out substantial momentum–conserving phases. An important consideration here is that many processes other than direct Coulomb collisions may rapidly equilibrate electron and ion temperatures. Faucher-Giguère & Quataert (2012) attempt to put limits on the incidence of such collisionless coupling by appealing to observations of the solar wind, but this is an area of considerable physical uncertainty.

Another way of using observations to decide if shock cooling is effective is to look for the inverse Compton spectral component directly revealing the cooling. Bourne et al. (2013) argue that the apparent lack of such a component in most AGN spectra rules out cooling shocks. But we recall from Section 3.3 that the coverage of UFOs is extremely sparse. Actually observing a collision and so the inverse Compton emission is inevitably a very rare event. It appears that observationally ruling out Compton shock cooling is so far inconclusive.