Annu. Rev. Astron. Astrophys. 2015. 53:115-154 Copyright © 2015 by Annual Reviews. All rights reserved

5. THE M − σ RELATION

We are now equipped to discuss the impact of a UFO on the host interstellar gas. We already noted that the wind impact implies a pair of shocks each side of the contact discontinuity between the wind and the host ISM. Initially the wind shock is close the hole, and we assume that inverse Compton cooling from the AGN radiation field cools it rapidly and puts the flow in the momentum–driven regime. The region of gas between the wind shock and the contact discontinuity, where it impacts and sweeps up the host ISM, is very narrow (cf the upper panel of Figure 8). The outer shock accelerating the ISM is also strongly cooled, so that the ‘snowplow’ region of swept–up ISM is narrow as well. So we can treat the whole region between the inner and outer shocks as a single narrow, outward–moving gas shell, whose mass grows as it sweeps up the host ISM (see Fig. 9).

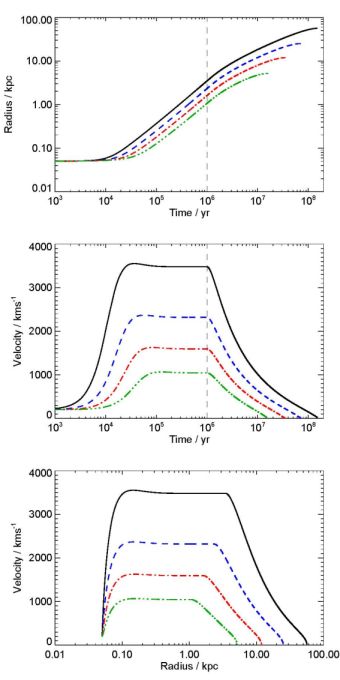Figure 9. Evolution of an energy–driven shock pattern for the case σ = 200 km s−1, fg = 10−2 computed numerically from the full equation (46). Top: radius vs time, middle: velocity vs time, bottom: velocity vs radius. The curves refer to different initial conditions: black solid – R0 = 10 pc, v0 = 400 km s−1; blue dashed – R0 = 100 pc, v0 = 1000 km s−1; red dot–dashed – R0 = 50 pc, v0 = 200 km s−1. All these solutions converge to the attractor (48). The vertical dashed line marks the time t = 106 yr when (for this case) the quasar driving is switched off. All solutions then follow the analytic solution (49). A case where the quasar remains on for a Salpeter times ∼ 4 × 107 yr would sweep the galaxy clear of gas. (From King et al. 2011).

As a simple model of a bulge, we assume that the matter of the host galaxy is distributed with an isothermal profile of velocity dispersion σ, with mass density

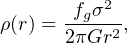(34)

so that the mass within radius R is

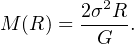(35)

A distribution like this is expected if the bulge results from mergers. For a roughly constant gas fraction f_g, the mass of the narrow swept–up gas shell at radius R is

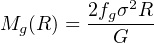(36)

so that the shell has the equation of motion

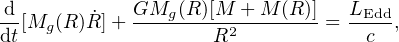(37)

where M is the SMBH mass. From (35, 36) and the definition of L_Edd (equation 17) this simplifies to

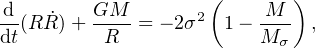(38)

where

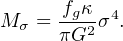(39)

Multiplying through by R and integrating once gives the first integral

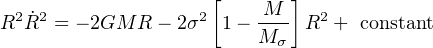(40)

For large R we have

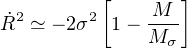(41)

which has no solution for M < M_σ. Physically this says that if the SMBH mass is below M_σ the swept–up shell of interstellar gas cannot reach large radius because the Eddington thrust of the black hole wind is too small lift its weight against the galaxy bulge potential. The SMBH cannot remove the gas from its surroundings, and goes on accreting. Any gas shell it drives outwards eventually becomes too massive, and so tends to fall back and probably fragment. This is likely to stimulate star formation in the shell remnants.

The precise value M_σ depends on the average gas fraction f_g. For a protogalaxy forming at high redshift we expect f_g = Ω_baryon / Ω_matter ≃ 0.16 (Spergel et al. 2003). Galaxies forming at later times may have larger f_g if they have gained a lot of gas, or smaller f_g if they have been largely swept clear of gas, or have turned a lot of their gas into stars. With the gas fraction f_g fixed at the cosmological value f_c = 0.16, the expression

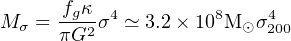(42)

is remarkably close to the observed relation (2), even though it contains no free parameter. We shall see in Section 5.5 why observations tend to give an exponent of σ slightly larger than the value 4 derived here. This agreement strongly suggests that SMBH growth stops at this point, although we must do some more work to show this (see Sections 5.2, 5.3 and 5.5 below).

The derivation here took the simplest possible description of a galaxy spheroid as an isothermal sphere (cf equation 35). We should ask if things change significantly if the galaxy bulge is more complicated than this. If the potential is spherically symmetric but the cumulative mass M(R) is not simply linear in R, we still get a first integral of the equation of motion (37) simply by multiplying through by M(R), giving the giving the condition for a swept–up momentum–driven shell to reach large radii. Relations very like (42) emerge in each case, so we expect qualitatively similar behavior. McQuillin & McLaughlin (2012) show this explicitly for three widely–used density distributions (Hernquist 1990; Navarro et al. 1996, 1997; and Dehnen & McLaughlin 2005): the results are in practice scarcely distinguishable from (42).

Whatever the bulge geometry, the black hole always communicates its presence only through the ram pressure of its wind, so we are always dealing with strongly radial forces in the solid angles exposed to this wind (this is not true of gas pressure, as we shall see in Section 5.3). It is likely that the orientation of the accretion disc with respect to the host galaxy changes with each new episode of accretion (so–called chaotic accretion, King & Pringle 2006, King et al. 2008), tending to isotropize the long–term effect of momentum feedback. Together with the sudden huge increase in the spatial scale as the critical black hole mass is reached (see the next Section) this may explain why the simple spherically symmetric prediction (42) seems to give a surprisingly accurate estimate of the critical mass.

5.2. What Happens When M = M_σ?

The result (42) is so close to observations that it strongly suggests that feedback somehow cuts off the growth of the black hole at a mass very close to this value. Some feeding may continue from gas in the immediate vicinity of the hole which is too dense to be affected by the ram pressure of the black hole wind. A thin accretion disc has this property for example, but cannot have a gas mass larger than ∼ (H / R)M ≪ M without fragmenting and forming stars.

But we still have to explain precisely how the gas is expelled. For example, one might worry that although momentum–driving can push the ISM away and inhibit central accretion, some kind of infall and SMBH accretion might restart shortly after momentum–driving is switched off, perhaps leading to alternating stages of quiescence and growth, eventually to masses far above M_σ. Observations show that black hole accretion occurs preferentially in gas–rich galaxies (cf Vito et al. 2014), so it seems that the black hole must largely clear the galaxy bulge of gas to terminate its growth. We will see later (Section 7) that if no other process than momentum–driving operated, this requirement would indeed lead to black hole masses significantly larger than M_σ, in conflict with observation.

This last point means that the way black hole growth influences the host galaxy must change radically when M = M_σ. It is straightforward to see why it should. We saw above that for M < M_σ the Eddington thrust cannot push the wind shocks to large R. As a result the wind shock remains efficiently Compton cooled, enforcing momentum–driving. It follows that the SMBH cannot stifle its own growth if M < M_σ. But all this changes once the SMBH exceeds the critical mass (42). Now even for a very small increment (O(R_inf / R_C) ∼ 10⁻²) of M above M_σ, a momentum–driven shell can reach the critical radius R_C. Crucially, this means that the wind shocks are no longer efficiently cooled: they become energy–driven. The shocked wind gas can now use all of its energy to push the interstellar gas as it expands into the host bulge. This motion becomes explosive and rapidly reaches kiloparsec lengthscales, comparable with the size of the bulge itself, rather the much smaller (parsec) scales of the momentum–driven phase.

So the real significance of the M − σ relation is that it marks the point where outflows undergo a global transition from momentum– to energy–driving.

5.3. Clearing Out a Galaxy: the Energy–Driven Phase

We know from (24) that an energy–driven outflow has more than enough energy to remove the interstellar gas entirely, and so presumably suppress further SMBH growth. Here we examine how this works in detail.

Once M > M_σ the outflow geometry changes completely (see Figure 8). The shocked wind region is no longer narrow (as in the upper panel of Figure 8), but large and expanding because of its strong thermal pressure (lower panel of Figure 8). The shocked wind’s thermal expansion pushes its shock inwards where it must hover at the cooling radius R_C (Zubovas et al. 2013). If it tries to move within R_C, momentum driving instantly pushes it out again (remember M > M_σ).

The shocked wind rapidly evens out its internal pressure as it expands at its sound speed ∼ 0.03c, so we take this pressure P as uniform over this region (but changing with time). The contact discontinuity at the outer edge of the shocked wind sweeps up the surrounding shocked ISM as before, but now has the equation of motion

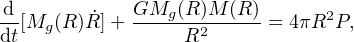(43)

where the pressure P is much larger than the ram pressure ρ v² appearing in (37). In the second term on the lhs we have neglected the contribution GM_g M / R² of the black hole gravity, as R ≫ R_C > R_inf. To make the problem determinate we need the energy equation. (This did not appear explicitly in the momentum–driven case because it was equivalent to the defining condition that all the wind energy not associated with the ram pressure was rapidly lost to radiation.) Here the energy equation constrains the pressure P by specifying the rate that energy is fed into the shocked gas, minus the rate of PdV working on the ambient gas and against gravity:

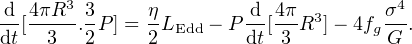(44)

We take a specific heat ratio γ = 5/3, use (23) for the energy input from the outflow and (35) to simplify the gravity term GM(R)M(R) / R². Now we use (43) to eliminate P from (44), and replace the gravity terms as before using the isothermal expression for M(R). We take the AGN luminosity as lL_Edd to allow for small deviations from the Eddington value. This gives

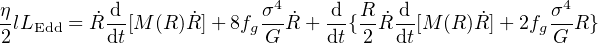(45)

and so

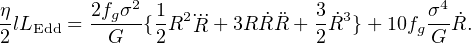(46)

This describes the motion of the interface (‘contact discontinuity’ in the lower panel of Figure 8) between wind and interstellar gas in the energy–driven case, replacing equation (37) in the momentum–driven case.

The energy–driven regime applies as soon as the SMBH mass reaches M_σ, and we will see that the host ISM is now quickly removed. We assume M = M_σ in L_Edd, and see that (46) has a solution R = v_e t with

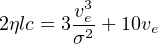(47)

The assumption v_e << σ leads to a contradiction (v_e ≃ 0.01c >> σ), so

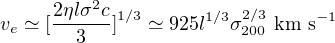(48)

This solution is an attractor. Figure 9 shows that all solutions quickly converge to it, regardless of initial conditions. Physically, its meaning is that if shock cooling is ineffective, the extra gas pressure accelerates the previously momentum–driven gas shell to this new higher velocity. Figure 9 also confirms that if the driving by the AGN switches off when the contact discontinuity is at radius R₀, it decelerates as predicted by the analytic solution of (46) with L_Edd = 0 found by King et al. (2011):

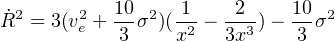(49)

where x = R / R₀ ≥ 1. Noting that v_e depends only weakly (as v_e ∼ l^1/3) on the luminosity, these results show that fluctuations – or even the intermittent disappearance – of the AGN luminosity have almost no effect on the outflow once it has started, because the flow still has a large reservoir of thermal energy available for driving. In particular an outflow can persist long after the central AGN has turned off, and the real agency driving an observed outflow may have been an AGN even if this is currently observed to be weak or entirely absent.

The solutions (48) or (49) describe the motion of the contact discontinuity where the shocked wind encounters swept–up interstellar gas (see Figures 8 and 9). This interface is strongly Rayleigh–Taylor (RT) unstable, because the shocked wind gas is highly expanded and has much lower mass density than the swept–up interstellar gas outside it, so that we have a light fluid underneath a heavy one. The RT instability leads to strong overturning motions even on small scales, and so is difficult to handle numerically. Deductions concerning the mean velocity and energy of the outflow, and its average spatial scale R(t), are likely to be believable, and agree closely with observations (see below) but we should be very cautious about results depending strongly on the detailed nature of the interface between the shocked wind and the swept–up interstellar medium. The RT instability is probably the reason that the high–speed (∼ 1000 km s⁻¹) outflows with prodigious mass rates we predict here are generally seen with much of the outflowing gas in molecular form. Apparently the interstellar gas entering the forward shock is efficiently cooled by two–body radiation processes. A preliminary analysis (Zubovas & King 2014) suggests that the interstellar gas overtaken by the forward shock is likely to have a multiphase structure. Most of it cools all the way from the shock temperature ∼ 10⁷ K back to low temperatures, ending in largely molecular form, even though it is entrained in an outflow with the ∼ 1000 km s⁻¹ velocity of the forward shock. But cooling is affected by the topology of the gas flow and the total area of interfaces between different gas phases. A full numerical calculation of this is currently impossible, so for the time being we can only make comparison with simple estimates, as here.

The mass outflow rate is fixed by how fast the outer shock overtakes the ISM and entrains new interstellar gas ahead of the contact discontinuity. The ISM ahead of the shock is at rest, so this runs into it at a speed giving a velocity jump by a factor (γ +1) / (γ −1) in the shock frame (where γ is the specific heat ratio: see e.g. Dyson & Williams 1997 for a derivation). This fixes its velocity as

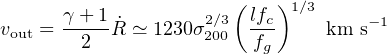(50)

(where we have used γ = 5/3 in the last form, and f_c ≃ 0.16 is the cosmological value of f_g). This implies a shock temperature of order 10⁷ K for the forward (ISM) shock (as opposed to ∼ 10^{10 − 11} K for the wind shock). Since the outer shock and the contact discontinuity were very close together as energy–driven flow took over from momentum–driven flow (see Figure 8) this means that the outer shock is at

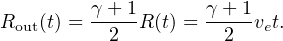(51)

This gives the mass outflow rate as

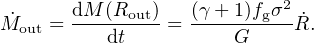(52)

For comparison the mass rate of the black hole wind, assuming M = M_σ, is

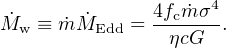(53)

This is much smaller than the outflow rate _out it drives, so we define a mass–loading factor as the ratio of the mass flow rate in the shocked ISM to that in the wind:

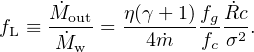(54)

Then we have

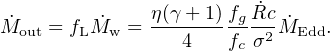(55)

If the AGN radiates at a luminosity ∼ L_Edd, we have = v_e, and (48) gives

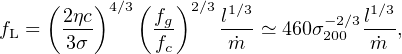(56)

and

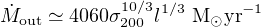(57)

for typical parameters, f_g = f_c and γ = 5/3. The total gas mass in the bulge is roughly M_g ∼ 10³ f_g M_σ (from equation 1). Clearly if the outflow persists for a time t_clear ∼ M_g / _out ∼ 1 × 10⁷ σ₂₀₀^2/3 l^−1/3 yr it will sweep away a large fraction of the galaxy's gas. The precise outflow duration needed for this depends on both the type and the environment of the galaxy, in practice leading to three parallel but slightly offset M − σ relations (see Section 5.5 below).

Equations (50, 57) give

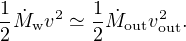(58)

So most of the wind kinetic energy ultimately goes into the mechanical energy of the outflow, as we would expect for energy driving. The continuity relations across the contact discontinuity show that if the quasar is still active, the shocked wind retains 1/3 of the total incident wind kinetic energy _w v²/2, giving 2/3 to the swept–up gas represented by _out.

Equation (58) means that the swept–up gas must have a scalar momentum rate greater than the Eddington value L_Edd / c, since we can rewrite it as

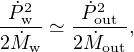(59)

where the 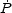's are the momentum fluxes. With 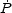_w = L_Edd / c, we have

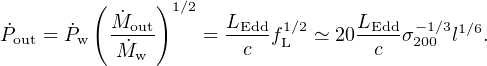(60)

Observations of molecular outflows consistently show _out v_out > L_Edd / c, and in particular Cicone et al. (2014) find that momentum rates 20L / c are common. This is an inevitable consequence of mass–loading (f_L > 1). These high momentum rates are important, as they are probably the way that the galaxy resists the accretion that cosmological simulations suggest still continues at large scales (Costa et al. 2014).

Recent infrared observations show abundant evidence for molecular outflows with speeds and mass rates similar to (50) and (57). Feruglio et al. (2010), Rupke & Veilleux (2011) and Sturm et al. (2011) find large–scale (kpc) flows with v_out ∼ 1000 km s⁻¹) and _out ∼ 1000 M_⊙ yr⁻¹) in the nearby quasar Mrk 231. Other galaxies show similar phenomena (cf Lonsdale et al. 2003, Tacconi et al. 2002, Veilleux et al. 2009 Riffel & Storchi-Bergmann (2011a, b) and Sturm et al. 2011: see Tables 1 and 2 of Zubovas & King 2012a for a detailed comparison with the theoretical predictions). In each case it appears that AGN feedback is the driving agency. 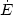There is general agreement for Mrk 231 for example that the mass outflow rate _out and the kinetic energy rate _out = _out v_out² / 2 are too large to be driven by star formation, but comparable with values predicted for AGN feedback.

It appears that energy–driven outflows from SMBH which have just reached their M − σ masses should be able to sweep galaxy spheroids clear of gas. A robust observational test of this is the expected mechanical luminosity (cf equation 23)

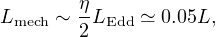(61)

where L = lL_Edd is the observed AGN luminosity. This is investigated by Cicone et al. (2014). As their Figure 12 shows, observation does largely confirm the relation 61). If the AGN are close to their Eddington luminosities (so that L ∝ M ∝ σ⁴ and l ≃ 1), the clearout rate ∝ σ^10/3 (equation 57) should scale linearly with the driving luminosity L. Figure 9 of Cicone et al. shows evidence for this correlation, with normalization close to that predicted.

5.4. Effects of a Galaxy Disc: Stimulated Star Formation and Outflow Morphology

We have so far discussed galaxy spheroids in isolation. This is in line with the observational evidence (see Kormendy & Ho 2013 for a review) that the SMBH scaling relations apply only to this component of a galaxy, and are essentially unaffected by the presence of a galaxy disc. In particular we suggest that the critical M − σ black hole mass is set by small–scale momentum–driven outflows interacting with only a very small central part of the bulge. But the energy–driven outflows we considered in the last subsection are global: they expand to far greater scales, and unless the galaxy is an elliptical must inevitably encounter its disc as they expand. In a gas–rich galaxy the gas in the innermost disc at radius R₀ must be close to self–gravitating. Assuming that the potential is roughly isothermal, it is straightforward to show that this implies a gas density ∼ ρ_d ∼ 2σ² / R₀, i.e. greater than the bulge gas density by the factor ∼ 1/f_g ∼ 10. We see from equation (46) that higher gas densities mean lower spherical outflow velocities, as they meet greater resistance. So when an initially spherical outflow encounters a high–density gas disc it flows around it, over its plane upper and lower faces. But the pressure in the outflow is at least initially far higher than in the disc: we can read off the pressure at the contact discontinuity from equation (43) as

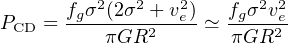(62)

and estimate the pressure at the forward shock into the ISM as

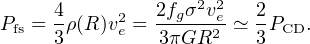(63)

By contrast the mid–plane pressure in a disc close to self–gravitating is

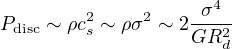(64)

where we have assumed the sound speed c_s ∼ σ and the self–gravity condition Gρ ∼ Ω² with Ω = √2σ / R_d the Kepler frequency at disc radius R_d. Thus when the outflow shock arrives at R = R_d its pressure is a factor ∼ (v_e / σ)² ∼ 25 larger than the disc's, and this remains true until the outflow shock has travelled out to radii R > R_d v_e / σ ∼ 5R_d. Any such compression must trigger a burst of star formation in the disc (cf Thompson et al. 2005, Appendix B), and here it rises to values

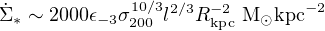(65)

(Zubovas et al. 2013), where є_∗ = 10⁻³є₋₃ is the efficiency of massive stars in converting mass into radiation, and we have substituted for v_e using (48). Zubovas et al. (2013) show that this leads to a starburst of total luminosity

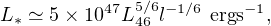(66)

where L₄₆ is the AGN luminosity in units of 10⁴⁶ erg s⁻¹. Such systems would appear as ULIRGs.

This suggests that in a galaxy with both a bulge and a disc, the clearout phase leaves the galaxy bulge without gas, but may be accompanied by a starburst in the disc. Recent observations of dusty QSOs appear to show this, with the black hole mass already on the M − M_b relation (1), and so fully grown (Bongiorno et al. 2014). In an elliptical on the other hand, clearout must leave the galaxy ‘red and dead’.

Since a galaxy disc is a major obstacle to an outflow, it follows that it may be able to divert a quasi–spherical outflow into a bipolar shape. This is particularly true in cases where the SMBH mass grows only a little, in a minor accretion event. Zubovas et al. (2011) suggest that the gamma–ray emitting bubbles disposed symmetrically about the plane of the Milky Way (Su et al. 2010) may be the remnants of a relatively recent and rather weak event like this.

5.5. The Three M − σ relations

So far in this Section we have seen that the arrival of the black hole mass at the M − σ relation means that its feedback makes a radical change from momentum–driving to energy-driving. The energy–driven phase which clears the gas from a galaxy bulge is short and violent. But it is clear that the black hole must inject a non–negligible amount of energy to eject the gas, and this requires accretion energy, i.e. some black hole mass growth. Evidently if the mass increment ΔM needed for this is ≫ M_σ we will have failed to explain the M − σ relation.

The mass increment Δ M is influenced by two factors. First, it must require significantly less SMBH growth to remove the gas from a spiral galaxy with a relatively small bulge, than for example an elliptical, where the much larger bulge mass means that energy–driving by the central SMBH wind must continue for longer in order to expel the remaining gas. Zubovas & King (2012b) find that energy–driving, and therefore SMBH mass growth above M_σ, must continue only for about 4 Myr (about 0.1 Salpeter times) in a typical spiral, but for for about 2 Salpeter times in an elliptical. So the final SMBH mass in a spiral is close to M_σ but in an elliptical it can reach

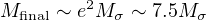(67)

The second factor affecting M, M_b is the galaxy environment. Cluster ellipticals can gain gas as they orbit through the intracluster gas. Some Brightest Cluster Galaxies (BCGs), which are near the centre of the cluster potential, are known to contain unusually massive SMBH (McConnell et al. 2011). Taking account of the extra black hole mass growth required to remove the bulge, and the mass a galaxy may gain from its surroundings, implies three parallel but slightly offset M − σ relations for spirals, field and cluster ellipticals (see Fig. 10). In principle there is also a relation for cluster spirals, but these are rare. We see from the Figure that the spread in offsets means that an observed sample drawn from galaxies of all three types would tend to produce a slope slightly bigger than the individual ones for each type, perhaps accounting for the slight discrepancy between the observed overall slope α = 4.4 ± 0.3 and the theoretical value of 4. All three types of galaxies obey a similar M − M_b relation (1) within the errors, as growth of the SMBH above M_σ goes together with higher M_b.

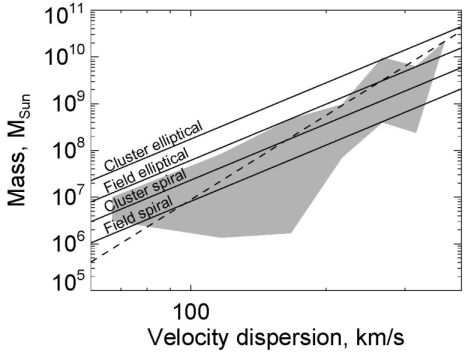Figure 10. The four (in reality three, as cluster spirals are rare) M − σ relations (solid lines) and their combined effect on observational fits (dashed line). All solid lines have slopes M ∝ σ4 and the dashed line has M ∝ σ6. The grey area is the approximate locus of data points in Figure 3 of McConnell et al. (2011). (From Zubovas & King 2012b).