


Astronomical distances have practically never been measured or numerically expressed with standard metric units, like m or km. First this would not be convenient units given the size of the solar system, let alone the distances of the stars or that of the galaxies. One could claim with good reasons that this can be resolved by a proper choice of multiples, and this will not put astronomy aside from the SI system. This is true and there is a more fundamental ground for the use of an independent and consistent system of units in astronomy.
Except in very limited and relatively recent instances with radar and laser ranging in the solar system, measured space quantities in astronomy are always angles and not lengths or distances as it is on the Earth. Therefore distances are derived quantities and byproducts of astrometric measurements attempting to detect small angular shifts in the direction of a celestial body resulting from its observation from at least two different points, as distant as possible from each others. The baselines, the Earth's radius or the size of the orbit of the Earth around the Sun, were not necessarily known in metric units with an accuracy matching that permitted with the angular measurements. This issue is more important in the solar system than it is for the stars and the galaxies, for which no extreme fractional error is achievable, even today with Gaia, the on-going ESA Astrometry mission, or the HST (Hubble Space Telescope), the only providers of direct and accurate measurements of stellar distances in the visible, although radio astronomy can do even better on a small number of galactic H2O or OH masers [4].
In the solar system the relative size of the planetary orbits was known to a good accuracy even before the discovery of the third Kepler’s law, relating the orbital period to the distance to the Sun. From pure angular observations it was possible at the time of Copernicus to build a model of the solar system showing the orbit of Mars or Venus with their correct scale compared to the Earth with a precision of about 5%. However the absolute scale expressed either in Earth radii, feet or toises was not possible without loss of accuracy. This situation worsened, in some sense, when orbits could be computed with the laws of gravitation as the relative accuracy greatly improved and the gap between the relative and absolute size widened. The need to use a reference of length disconnected from the standards used for trade or scientific usage became mandatory to benefit fully from the accurate astrometry.
2.2. The astronomical system of units
Starting in the 19th century and made official by IAU in 1938, the astronomical unit was defined as a fundamental constant of the astronomical system of units as a length such that the Gravitational constant is the square of the defining Gauss constant,
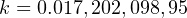 |
(1) |
yielding,
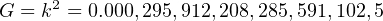 |
(2) |
with the unit of mass being the solar mass and the unit of time the solar day of 86,400 seconds. Combined with the Kepler’s third law,
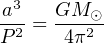 |
(3) |
Eq. 1, implies that the mean motion of a massless planet orbiting the Sun at one astronomical unit is k rad day−1, corresponding to a period of
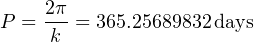 |
(4) |
very close to the sidereal year. Therefore the au defined by Eqs. 1-3 agrees with the simple initial idea of the astronomical unit being essentially the mean distance between the Earth of the Sun, or the semi-major axis of its orbit, although this is not formally its definition. With the above definition and units, the law of attraction reads,
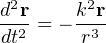 |
(5) |
This allowed astronomers to produce very accurate numerical or analytical theories of the motion of solar system bodies and predict their positions without having their absolute distances. The whole system is consistent and angular observations constrain the free constants of the model, primarily the position and velocity vectors of the bodies at an arbitrary epoch.
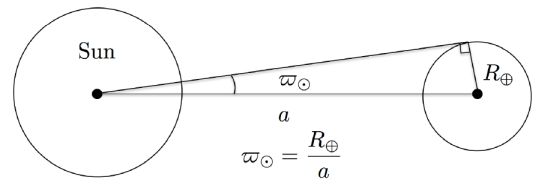 |
Figure 1. Definition of the solar parallax. |
The absolute length of the au was derived from dedicated observations as an angular quantity called the solar parallax whose meaning is shown in Fig. 1. The measurement of the angle ϖ⊙ being equivalent to the Sun distance expressed with the Earth’s radius. The latter being known in common unit, the procedure would yield the size of the solar system in the same unit. Assessing this length remained a central issue in astronomy until very recently and was even referred to as the noblest problem in astronomy by G. B. Airy, the Astronomer Royal from 1835 to 1881. With the law of motion, a single measurement of a distance of one solar system body suffices in establishing the absolute scale of the solar system. The very first significant step in this direction was achieved in 1672 during a most favourable (small distance) opposition of Mars, making its parallax as large as possible. On the 04 September 1672, Mars approached the Earth at 0.381 au, very close to the smallest possible distance of 0.371 au. Observing from two distant points J.D Cassini in Paris and J. Richer in Cayenne found an equatorial parallax of 10′′, or
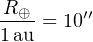 |
(6) |
giving, 1 au ≈ 1.32 × 108 km. This is too small by ≈ 10%, but for the first time astronomers had a sensible estimate of the real size of the solar system from a method whose principle was sound and could not be disputed.
The rare transits of Venus across the solar disk offered another way of ascertaining the au as noted first by J. Gregory in 1663 and widely heralded by E. Halley in 1716. The advantage of Halley's proposal is still extant since he proposed to replace pure angular measurements by timings of the moment the dark disk of the planet is seen encroaching on the bright solar disk. Given the angular speed of Venus relative to the Sun it is easy to show that a better accuracy can in principle be reached with the timing than with classical position sights. Halley claimed that the transit duration could be assessed to few seconds of time and consequently the distance to the Sun to one part to few thousandths. International cooperation was put in place for every following occurrence of the Venus transit in 1761, 1769, 1874, 1882 to observe and time the passages from the most remote places on the Earth. This led to adventurous expeditions that have been reported in many books and most is available on-line or in popular accounts [5], [6].
Regarding the astronomical aim, the results were not on a par with the expectations and never reached the accuracy claimed by the illustrious astronomer. The extensive discussion of the four transits by S. Newcomb in 1892 ended up with a solar parallax of ϖ⊙ = 8.79′′ ± 0.018′′ (current determination 8.794143′′⋯) or a value for the Sun-Earth distance of (149.7 ± 0.3) × 106 km. This was in some sense a very unsatisfactory situation in regards of the achievements of the planetary theories at the same time and after the triumph of the solar system dynamics with the discovery of Neptune in 1846.
A fortunate circumstance cast some lights in a gloomy landscape with the discovery in 1898 of the minor planet Eros (433 Eros) simultaneously at Berlin and Nice, the first of the near-Earth objects to be identified. Eros comes within the orbit of Mars and favourable oppositions that repeat every 30 years may bring the planet to 0.2 au 1 from the Earth, closer than any other solar system object known at that time. The first such passage took place in 1901 and the next good one was in 1931. Again a broad international cooperation was set up to observe and reduce the observations and led to a solar parallax of ϖ⊙ = 8.790′′ ± 0.001′′. It was the most accurately known value for the solar distance at that time, and this value has remained the standard until mid-1960 when radar measurements gave a more accurate value for the distance to the Sun.
2.4. The astronomical unit today
Again a direct range measurement based on timing took precedence over classical angular measurements, with a measured quantity that was almost a distance, and no longer an angle. In particular there were no more reasons to express it as a parallax, a formulation inherited from the measurement technique, but a distance expressed directly in SI units, given the accuracy of the velocity of light. The distance became the primary quantity and the parallax a derived parameter. Later on the use of spacecraft tracking combined to highly accurate global numerical integrations of the solar system motions resulted into the best values of the astronomical unit ([7], [8], [9]), which eventually led the International Astronomical Union to recommend in 2009 (Resolution B2, IAU 2009 System of Units) a value of 149,597,870,700 ± 3 m for the au.
Eventually this was turned into a defining astronomical constant in the IAU 2012 Resolution B2 with the astronomical unit being a conventional unit of length strictly equal to 149,597,870,700 m in agreement with the value adopted in IAU 2009 Resolution B2 [10]. Accordingly the BIPM changed this unit from the table of non-SI units whose values in SI units must be obtained experimentally to the table of non-SI units accepted for use with the International System of Units. It is now tied to the meter with a fixed factor. In short this is now a multiple of the meter and what should be experimentally determined is the scale factor of the solar system, say the Sun-Earth mean distance expressed in au. A consequence is that to the equation of motion (5) one must substitute,
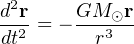 |
(7) |
with GM⊙ in m3 s−2 and the SI units or their multiples for length and time. Modern numerical integrations of the Solar System comply now with this requirement. As far as metrology is concerned the situation is clarified and it is left to the astronomers now to refine their measurements to give the size of the orbits in meters with the best accuracy.
1 The astronomical unit should be abbreviated as au since 2012 as stated in the recommendation of the International Astronomical Union in its Resolution B2. This is also the notation given by the BIPM in its official list of secondary units. It is usual to find instead AU or ua. Back.