


For centuries the problem of stellar distances has puzzled astronomers, although the underlying geometric principles needed to ascertain them were extremely simple and well understood. The basic idea is sketched out in Fig. 2 showing the apparent shift in the star position resulting from the annual motion of the Earth around the Sun.
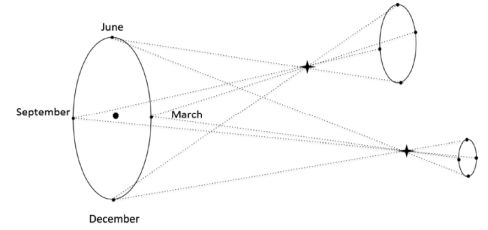 |
Figure 2. The parallactic motion for a nearby and a distant star. |
Provided the stars are not infinitely remote compared to the size of the Earth’s orbit, our annual displacement translates into a reflex apparent displacement of the stars on the sky, since during the year the different lines joining the observer to the star are not parallel. The farther the star, the smaller the parallactic ellipse, and more precisely its size is proportional to the reciprocal of the star distance. The parallax of a star is defined by the angle subtended at the star by one astronomical unit or half the apparent diameter of the Earth orbit when seen from the star. Mathematically one has for the parallax ϖ of a star at distance d from the solar system,
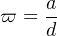 |
(8) |
where a = 1 au. The unit of distance is the parsec, noted pc and its common multiples are kpc, Mpc, Gpc. By definition of the parsec, a star at 1pc has a parallax of 1.0′′, meaning that its distance is 206,264 au, corresponding also to 3.26 light-years or 3.1 × 1016 km. With distances in pc and parallaxes in arcsec one has ϖ = 1 / d. No star has a parallax reaching one arcsec and the nearest star, Proxima Centauri with a parallax of 0.77′′ is at 1.30 pc from us. In astronomy one does not measure distances directly, but their angular signature with the parallax. Hipparcos and Gaia deliver parallaxes from which distances are inferred. But the parallax is the best way to ascertain distances within the Galaxy without any assumption regarding the physics of the source, although this is not the only mean to do it. However this is the only way to do it on large number of stars in a survey mode, while the alternative method needs eclipsing binary stars with good spectroscopy, a relatively rare instance.
Given the definition of this unit of distance, it is clear that both the measured parallaxes and the distances expressed in parsec are independent of the precise knowledge of the au in metric units and would not change with an improvement of the au. This is a direct expression of the angular shift on the sky with a distance given in Sun-Earth distance. Using lightyear would have been an option, but nothing in the measurement principle would allow to link naturally the parallax to the light travel time and simply to the finite speed of the propagation of light. The choice of the pc has been discussed around 1910 and made official by the IAU in 1925. Within the Galaxy distances are given in pc or kpc, while extragalactic distances are in Mpc. Beyond few Gpc the redshift, which is the measured quantity, is more usual. Also the distance modulus given in Eq. 15 is convenient when photometric data are involved. The diameter of the Milky Way is about ≈ 30 kpc and the Sun is located at ≈ 8 kpc from the galactic centre. The Andromeda galaxy, our nearest external major galaxy, lies at 0.78 Mpc and has a distance modulus of 24.5 mag.
It is also important to stress that in the heliocentric theory detecting the parallactic motion is a proof of the Copernican doctrine, and conversely its opponents exploited the lack of detection to support alternative theories and to challenge the doctrine. Therefore the signature of the Earth’s motion was primarily searched for fundamental reasons rather than to learn about the size of the Universe. The Tycho planetary system was a partial answer to this absence of evidence and could not be opposed as long the parallax of the fixed stars, or any other proof of the Earth motion, was not seen. This came before the first stellar parallax was measured through the discovery of the stellar aberration in 1727 by J. Bradley, while he was himself engaged into the search of the stellar parallax.
The tiny parallactic motion shows up as a periodic change of spherical coordinates as,
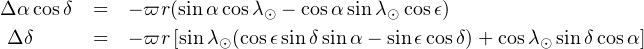 |
(9) (10) |
respectively for the star right-ascension and declination. Here, ϖ is the parallax (usually given in second or millisecond of degree), α, δ are the right-ascension and declination, λ⊙ the ecliptic longitude of the Sun, є the obliquity of the ecliptic and r the distance of the observer to the Sun in astronomical unit (always very close to unity, even with Gaia). The path described by the star on the sky is an ellipse of semi-axes ϖ, ϖ sinβ, where β is the ecliptic latitude. This is a circle at the ecliptic pole which degenerates into a straight segment of length 2ϖ in the ecliptic plane.
In an ideal world, parallaxes could be found by sampling the equatorial coordinates of a star over a year and then extracting the amplitude of the yearly sinusoidal change in one or both coordinates. But the amplitude is at most 0 .′′ 7 in the most favourable case and two to three orders of magnitude smaller for a typical galactic star. In addition there are other sources of change in the star coordinates which must be accounted for and the parallax is usually a small fraction of the whole motion. Getting accurate absolute parallaxes is nearly hopeless with ground-based observations given the adverse effect of the refraction, the telescope flexure and the difficulty to refer observations to an invariable frame of reference during the year.
As noted by Galileo resorting to a small field offered a route to success. Instead of measuring the absolute displacement in a well defined reference frame, one could detect the tiny parallactic motion with respect to one or few neighbouring stars with the additional assumption that these reference stars are far more distant than the star whose parallax is searched. In short the measurement is no longer ϖ but the difference between the parallax of the nearby star and that of the reference star(s). One gets at the end a relative parallax instead of an absolute parallax, as long as one cannot tell how far is the reference star to correct the result for this bias. After many failed attempts, the German astronomer and mathematician F.W. Bessel made the first successful parallax measurement ever, for the star 61 Cygni which he found equal to 0.314′′ (0.285′′ ± 0.0005′′ with Hipparcos and 0.28615′′ ± 0.00006′′ with Gaia for 61 Cygni B), or a distance of 3.2 pc (10.3 lightyears).
This marked the start of a systematic and difficult search which is still on-going today with better instruments placed outside the Earth's atmosphere. This allowed astronomers to get about 100 measured parallaxes by the year 1900 with a relative accuracy better than 50%. The number grew steadily during the 20th century, as shown in Table 1, but this remained a painstaking task with low yielding, although the use of photographic plates from ≈ 1920 onwards relieved observers from long hours at the eyepiece in the near open air, traded for equivalent long hours at the measuring machine in the comfort of a laboratory. See [11] for a discussion of the state of the art around 1910.
| Year | number | notes |
| 1840 | 3 | 61 Cygni, Vega, α Cent |
| 1850 | 20 | |
| 1890 | 40 | |
| 1910 | 300 | with 52 photographic parallaxes |
| 1925 | 2000 | photographic plates |
| 1965 | 6000 | Yale catalogue |
| 1980 | 8000 | just before Hipparcos |
The large scatter of the measurements carried out on the same stars by different observers and different methods gives an idea of the systematic errors. The fourth, and last, version of the Yale Catalogue of Trigonometric Parallaxes [12], the reference in the field before Hipparcos, gives the trigonometric parallaxes for 8112 stars with a mode in the quoted accuracy of 0.004′′, an improvement of a factor three compared to the previous release of 1963. To appreciate the difficulty to obtain parallaxes with ground-based astrometric techniques, in the interval of 32 years between the two publications only 1,722 stars were added.
In any case the number of reliable trigonometric parallaxes, say better than 10% in relative uncertainty, stayed below ≈ 2000 before the launch of Hipparcos and remained limited to bright stars. This was really very small in comparison with the contemporary sky surveys listing several 100’s million of stars with positions and some basic photometric information. Of course the trigonometric parallaxes were not the only distance estimator available, but this was the only way to get a geometric measurement of the parallax free of any assumption on the physics of the stars, and any other method had to be calibrated on reliable distances and ultimately rested upon this small set of trigonometric parallaxes.
3.2. The Hipparcos parallax survey
Hipparcos (see for reviews [13], [14]) opened a new era for astrometry thanks to the access to space to do accurate astrometric observations without the limitations caused by the bending and twinkling of light rays by the Earth’s atmosphere. The key ideas to carry out absolute astrometric measurements from space can be traced back to the French Astronomer Pierre Lacroute in the mid-1960s. He realised that a census could be carried out with almost uninterrupted observations allowing to triangulate the heavens with long arcs between pairs of stars. The most important and novel idea was to observe simultaneously two fields of view in very widely separated directions. Combining these two lines of sight onto a single focal plane would lead to a rigid network of stellar positions covering the whole celestial sphere, provided one could guarantee the stability of the angle between the two directions.
This was still basically relative astrometry, but not the way astronomers were used to, thanks to the wide angular separation between the two directions. The phase of the parallactic ellipses in each direction would be different and stars linked by the wide angle would change from time to time. At the end one could reconstruct the 2-D position of each star at a reference epoch and solve for their motion and absolute parallax, at the expense of a global adjustment incorporating all the observations. After a long process of maturation, feasibility assessment, technical studies and lobbying, the Hipparcos project was selected in the European Space Agency’s science program in July 1980 and eventually the satellite was launched in August 1989. The scientific goal was to reach a 2 milliarcsec (herein abbreviated as mas for 0.001′′) accuracy for about 100,000 stars, selected on the basis of their astrophysical interest, survey coverage at around 8.5 mag and ability of Hipparcos to observe them repeatedly during its planned mission of two years. The launch was dramatic and near fatal to the mission due to the failure to fire the apogee motor needed to reach the geostationary orbit. This ended up with the satellite on a wrong orbit, from which virtually nothing valuable was believed achievable and a life-expectancy much reduced due to the daily crossing of radiation belts. Eventually the mission scenario was adapted and successful operations lasted until march 1993 when to much accumulation of hig-energy particles fatally impaired the electronic. The final results published by ESA in June 1997 [15] surpassed the expectations placed on the satellite at its acceptance and this has even been improved ten years later by a new data reduction almost single-handed by F. Van Leeuwen [16].
The publication gave the astronomical community a brand new astrometric catalogue of 120,000 stars, all accurate in position and parallaxes to about one thousand of a second of arc (two times better than the initial objective) and supplemented with photometric [17] and double star data [18]. On top of that came also a less accurate but much larger catalogue of 2.5 million stars called Tycho-2 [19] resulting from measurements made with the Hipparcos star detector and the combination with the almost one-century-old photographic plates of the Carte du Ciel sky mapping.
Concentrating on the main topic of this review, Hipparcos astrometry was a truly new start for parallax survey. The total number of trigonometric parallaxes rose at once to more than 100,000, with nearly 50,000 better than 20% in fractional errors (σϖ / ϖ < 20%) and 20,000 at the 10% level. The reference frame was made inertial by linking the whole system to extragalactic sources, using radio stars common to Hipparcos and radio observations, or of observations of quasars relative to nearby Hipparcos stars [20]. This was an epoch-making advance in astrometry and in the measurement of stellar distances. Application to luminosity calibrations for a large variety of stellar types followed closely the publication and set the pace to improvements of the second rung of the distance ladder. More generally the Hipparcos data have influenced many areas of astronomy such as the the structure and evolution of stars and the kinematics of stars and stellar groups, the distance of the Hyades cluster, the galactic rotation from Cepheid variable stars, albeit the limited sample size of sources and observed volume. The outstanding and in-depth review by Perryman [21] based on most of the papers published in 1997-2007 using the Hipparcos catalogue provided an amazing detailed survey of the application of Hipparcos to stellar and galactic physics. The stellar distances and accurate proper motions together with the high-precision multi-epoch photometry are the crucial data exploited in these papers.
Hipparcos was a resounding and acclaimed international success allowing the Europeans to quickly submit several more ambitious proposals for space astrometry, at the same time as others were also submitted to NASA or to the Japanese space agency [22]. Only one of these proposals survived the various examinations by selection committees and Gaia was eventually selected as a cornerstone mission in April 2000 for a launch around 2011.
The basic concept is directly drawn from Hipparcos, but with a much larger telescope (actually two telescopes), a mosaic of 106 CCD detectors replacing the outdated photoelectric detector of Hipparcos. Two other instruments were added to carry out spectrophotometry and spectroscopic measurements, the latter to measure the velocity along the line of sight. While Hipparcos catalogue was limited to 100,000 pre-defined stars brighter than 13.2 mag, Gaia was designed to realise a sensitivity-limited survey to 20 mag. Hipparcos could only take a star at a time while Gaia is able to record simultaneously several 10000s images mapped on its focal plane. About one billion stars, amounting to ≈ 1 percent of the Milky Way stellar content, are expected to be repeatedly observed during the nominal 5-year mission, with a final astrometric accuracy of 25 µas at G = 15 mag. (1 µas = 0.001 mas = 10−6 arcsec).
Gaia's main scientific goal is to clarify the origin and history of our Galaxy, from a quantitative census of the stellar populations and extremely accurate astrometric measurements to derive proper motions and parallaxes. See [23] for the proposal and [24] for a presentation of the actual mission, the spacecraft, the operations and the data acquisition strategy. The principle of the scanning satellite relies on a slowly spinning spacecraft to measure the crossing times of stellar images transiting on the focal plane. As for Hipparcos, there are two fields of view combined onto a single focal plane where astrometric measurements are done. The time relates the one-dimensional star position to the instrumental axes. The relation to the celestial frame is obtained with the satellite attitude, which is solved simultaneously with the star positions in a global solution as described technically by Lindegren et al. [25].
The Gaia satellite was launched on 19 December 2013 and the science data collection started after the in-flight qualification on 25 July 2014. A first batch of results was released on 15 September 2016 with only 14 months of data processed. This release comprised primarily a position catalogue (only two position parameters per source) for 1.14 billion stars, the largest ever such collection. A smaller catalogue combining Gaia and Hipparcos included parallaxes and proper motions for ≈ 2,000,000 stars with a sub-mas accuracy [26]. The release contained also variable stars and a set of 2200 quasars common to Gaia and the radio ICRF [27] used to align the Gaia and radio frames. Therefore the Gaia reference frame and ICRF are nominally identical.
In April 2018 the 2nd release came out with parallaxes for nearly 1.4 billion stars [28], with a median uncertainty of 0.1 mas at G = 17 and 0.7 mas at G = 20. If we set the threshold for the usefulness of a distance to a relative precision better than 20%, at G = 17, Gaia DR2 reaches distances up to 2 kpc and 0.3 kpc at G = 20. The distribution of the parallax fractional uncertainty is shown in Fig. 3 in the form of ϖ/σϖ. One reads directly on the histogram that about 50 millions stars (out of 1.3 billion in the survey) have a relative precision in distance better than 10%, to be compared to 20,000 with Hipparcos. This again will increase around to 100 million in the more advanced releases.
This makes up the state of the art today regarding our knowledge of the stellar distances within our Galaxy from the geometric measurement of their parallaxes. Gaia found that there are 620,000 stars (more precisely unresolved stellar systems) within 100 pc and nearly 5200 at d < 20 pc. This gives a typical density of 0.15 star pc−3 in the solar neighbourhood. For a uniform and random distribution with ρ stars per cubic parsec, one computes easily the mean distance between two closest neighbouring stars as,
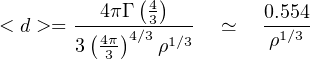 |
(11) |
yielding with the Gaia census to <d > ≈ 1.04 pc for the typical distance between a star and its nearest neighbour, not much different from the distance between the Sun and Proxima Centauri.
Although this data release uses only 22 months of data, while the nominal mission will have 60 and a possible extension of almost five years is likely, this parallax survey is by far the most comprehensive ever done and has no match in terms of size and accuracy, with the exception, regarding the accuracy, of a handful of radio masers observed with the VLBI technique. For the Galactic stars this is the crowning of nearly two centuries of parallax quest starting with F.W. Bessel in 1838. Until many years in the future there will be not such undertaking to get trigonometric parallaxes directly from astrometric observations and the Gaia survey is now actively being (see Sect. 4.3) used to reconstruct the whole distance scale beyond the Galaxy, based on secondary indicators.
I summarise in the next section the principles and ranges of applications of the numerous methods used today by astronomers to estimate distances from photometric indicators, but a major warning must be issued at this stage to any user deriving distances or other astrophysical parameters from the Gaia parallaxes. Better to read first the paper by Luri et al. ([29]) to guard against the numerous pitfalls to get a distance or a luminosity from the parallax. Only for the very accurate parallaxes (σϖ / ϖ < 0.1) the straightforward transformation d = 1/ϖ can be used safely. Otherwise a better statistical inference must be used to keep the bias under control.