


It is worth starting this review with a brief account of the dark matter candidate particles presently in the ballpark; one has to keep on mind however, that there are likely to risk not to be “the” DM particle.
2.1. Collisionless and cold dark particles
Let us start by recalling the motivations that have led to about 30 years of fascination with the Weakly-Interacting Massive Particles (WIMPs) and especially with the lightest supersymmetric particle (Steigman and Turner 1985, see also Kolb and Turner 1990). At high temperatures, (T ≫ mWIMP), WIMPs are thermally created and destroyed. As the temperature of the Universe decreases due to its expansion, the density is exponentially suppressed (∝ exp[−mWIMP / T]) and becomes no longer high enough to pair-create them. When the WIMP mean free path is comparable to the Hubble distance, the particles also cease to annihilate, leave the thermal equilibrium state and “freeze-out”. At this point, the co-moving density remains constant. The temperature for which the freeze-out occurs is about 5% of the WIMP mass. Therefore, the (relic) density becomes constant when the particles are non-relativistic. The value of the relic density ΩWIMP depends only on the total annihilation cross-section σA and the particles’ relative velocity |v|:
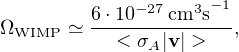 |
(2) |
The scale of weak interaction strength ( ∼ α2 / mWIMP2) implies that < σA |v| > 10−25 cm3 s−1, where σA is the cross section and the WIMP mass is taken to be 100 GeV. The resulting relic density for such a particle would be within a factor 3 of the measured value of the dark matter density Ωm (e.g., Planck Collaboration et al. 2016). This remarkable coincidence is referred to as the “WIMP miracle.” This particle, today, should interact with ordinary matter only through weak interaction, in addition to the gravitational one. The former should occur via the exchange of a scalar particle, or a vector boson interaction. These interactions together with the particle-particle annihilations ongoing in the densest region of the Universe, would make the particle detectable.
It is known that this scenario reproduces a wealth of cosmological observations, particularly on scales > 10 Mpc. On the other hand, WIMPs have so far escaped detection (see Figs. 2–3) and, furthermore, there is a number of small-scale issues that put in question their being the dark particle in galaxies.
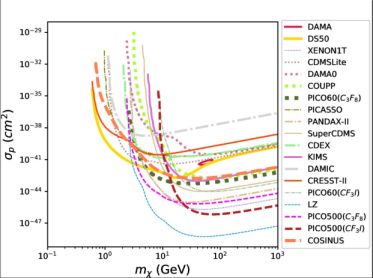 |
Figure 2. top Current 90% C.L. exclusion plots to the effective WIMP–proton cross section, see Kang et al. (2018). |
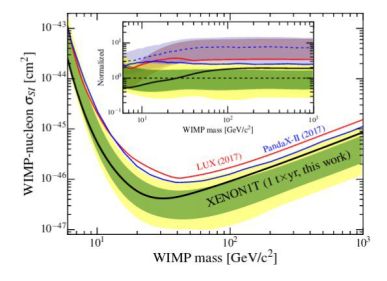 |
Figure 3. Current 90% C.L. exclusion plots to the effective WIMP–nucleon cross section. Image reproduced with permission from Aprile et al. (2018), copyright by APS. |
2.2. An unexpected new candidate for cold dark particles
There might be a connection between the dark matter in galaxies, in particular the cold DM and the gravitational waves produced by the merging of stellar-mass black holes and possibly detectable by LIGO-Virgo experiments. This is due to the intriguing possibility that DM consists of black holes created in the very early Universe. In this case, the detection of primordial black hole binaries could provide an unambiguous observational window to pin down the nature of dark matter (Green 2016). These objects are also detectable as effect of their continuous merging since recombination. This violent process can have generated a stochastic background of gravitational waves that could be detected by LISA and PTA (see also García-Bellido 2017).
It is known that massive primordial black holes form at rest with respect to the flow of the expanding Universe and then with zero spin. Moreover, they have negligible cross-section with the ordinary matter and constitute a right candidate for the ΛCDM scenario (see, however, Koushiappas and Loeb 2017). Of course, just substituting WIMPs with primordial BHs does not immediately relieve the severe tension with the observations at galactic scales that these particles have. It is, however open the question whether these primordial BHs could have some sort of interaction with baryons which is instead forbidden to WIMPs.
2.3. Self-interacting DM particles
Self-interacting dark matter (SIDM) particles were proposed by Spergel and Steinhardt (2000) (see also Boddy et al. 2014, Bode et al. 2004) to solve the core-cusp and missing satellites problems (see also Tulin and Yu 2017, Bellazzini et al. 2013). DM particles scatter elastically with each other through 2-2 interactions and, as low-entropy particles, are heated by elastic collisions within the dense inner halo and leave the region: the central and nearby densities are then reduced, turning an original cusp into a core. The collision rate is:
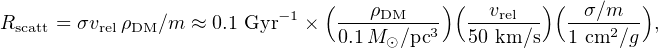 |
(3) |
where m is the DM particle mass, σ, vrel are the cross section and relative velocity for scattering. Within the central region of a typical dwarf galaxy we have: ρDM ∼ 0.1 M⊙ / pc3 and vrel ∼ 50 km/s. Therefore, the cross section per unit mass (σ / m) must be at least:
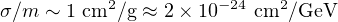 |
(4) |
to have an effect; this corresponds to about one scattering per particle over 10 Gyr galactic timescales. With the above value of σ / m, Rscatt is negligible during the early Universe when structures form. SIDM, therefore retains the success of large-scale structure formation of the ΛCDM scenario, and affects the dark structures on small scales only once they are already virialized.
The self-interacting dark matter is then a cusp-core density profile transformer (e.g., Vogelsberger et al. 2014, Zavala et al. 2013, Kaplinghat et al. 2015). As result of the annihilation among these particles in the denser inner regions of the galactic halos, the originally cuspy DM density becomes constant with radius. Outside the core region, the number of annihilations rapidly falls as ρDM2(r) and the halo profile remains identical to the original one.
The idea is that the dark matter is a scalar dark particle of mass ma ∼ 10−22 eV. At large scales its coherent macroscopic excitations can mimic the behavior of the cold dark matter (CDM). At the scale of galaxies, however, this particle has macroscopic wave-like properties that may explain the classic “discrepancies” of the standard DM scenario (Weinberg 1977, Hui et al. 2016, Bernal et al. 2017, Ringwald 2012).
Once in galaxies, these particles behave as Bose–Einstein condensate (BEC); in this model, the inter-particle distance is much smaller than their de Broglie wave length. The particles move collectively as a wave: their equation of state can lead to cored configuration like those observed. The capability to detect such Bose–Einstein-condensed scalar field dark matter with the LIGO experiment is under analysis (Li et al. 2017).
2.5. Warm dark matter particles
Warm dark matter (WDM) particle decouples from the cosmological plasma when it is still mildly relativistic. These particles can be created in the early Universe in a variety of ways (Dodelson and Widrow 1994, Shi and Fuller 1999, Kusenko 2009). In the case where the WDM consists of thermal relics, the suppression of small-scale power in the linear power spectrum (e.g., Bringmann et al. 2016) PWDM, can be conveniently parametrized by reference to the CDM power spectrum PCDM, see Fig. 4. In the more likely cases in which the WDM particle is a non-resonantly produced sterile neutrino, its mass msterile, can be related to the mass of the equivalent thermal relic (Viel et al. 2005). This conversion depends on the specific particle production mechanism.
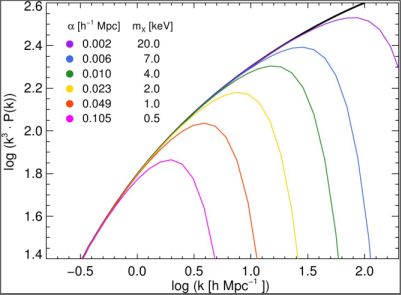 |
Figure 4. Linear power spectra in ΛCDM (black line) and ΛWDM (coloured lines) scenarios. ΛWDM models are labelled by their thermal relic mass and value of the damping scale α. We have (PWDM / PCDM)1/2 = [1 + (αk) 2/1.1] −5/1.1, k is the wave-number. Image reproduced with permission from Kennedy et al. (2014), copyright by the authors. |
Given the mass of this particle being about 2 keV, its de Broglie length-scale is of the order of 30 kpc, so that, inside the optical region of galaxies a quantum pressure emerges (Destri et al. 2013, de Vega and Sanchez 2017) and plays a role in the equilibrium of the structures. The DM particles follow, then, a Fermi–Dirac distribution:
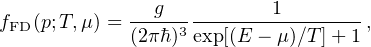 |
(5) |
where p and E = p2 / (2m) are the momentum and the single-particle kinetic energy; T(r), expressed in terms of energy, is the average temperature of DM particles at a radius r: T(r) ∝ V2(r) in spirals and T(r) ∝ σl.o.s.2(r) in pressure dominated systems. Noticeably, f(p) has an upper limit: f(p) ≤ g / (2π ℏ)3, where g is the number of internal degrees of freedom. We have, in this case, that the quantum pressure and not the Gravity Force shapes the inner DM density profile. WDM particles can be detected: they can produce a monochromatic gamma ray line at 2mWDM keV, which is constrained by X-ray measurements, e.g., Boyarsky etal.(2007).
The properties of WDM particles, their scientific case and cosmological role and the various strategies to detect them, have recently been presented in a White Paper (Adhikari et al. 2017).
2.6. In search for dark matter
For 30 years, WIMPs have been the first target in our attempt to detect and identify the dark particle. During the past decades, the sensitivity of the experiments involved has improved by three to four orders of magnitude, but an evidence for their existence is yet to come. On the other hand, searches at hadron colliders (which attempts to produce WIMPs through the collision of high energy protons and the subsequent formation of stable dark matter particles that can be identified through the production of quarks and gluons), have given no result (see Butler 2018).
It is agreed that no conclusive detection signal of the particle has yet arrived as result of a many year-long extensive search program that combined, in a complementary way, direct, indirect, and collider probes (see Arcadi et al. 2017 for a detailed review).
However, it is worth discussing astrophysical aspects, related to the above searches, that have an intrinsic importance and that are valid also for any particle investigation. In direct searches, the differential event rate Rscatt
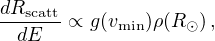 |
(6) |
is proportional to ρ(R⊙) the local (i.e., at the solar radius) dark matter density and to the function g(vmin) = ∫v > vminvesc [f(v) / v] d3 v. vmin is the minimum particle speed that can cause in the detector a recoil of energy E (Gondolo 2002).
vesc is the escape velocity from the Milky Way: vesc = (570 ± 120) km/s (Nesti and Salucci 2013). A reference value of ρ(R⊙) = 0.3 GeV/cm3 is often adopted however recent accurate determinations indicate a rather higher value: ρ(R⊙) = (0.43 ± 0.06) GeV/cm3 (Salucci et al. 2010, Catena and Ullio 2010).
To obtain g(vmin), one needs the whole DM density distribution, however, for the Milky Way, we can consider the galaxy halo as an isotropic isothermal sphere with density profile ρ(r) ∝ r−2. Then f(v) = [N / 2 π σv2] exp(− v2 / 2 σv2), where N is a normalization constant and σv is the DM particles one-dimensional velocity dispersion, which in the present model is related to the circular velocity V(r) by: σv = V(r) / √2.
The indirect searches of DM are based on astrophysical observations of the products of the DM particles self-annihilation (or decay) able to climb up the emissions coming from the likely astrophysical mechanisms also producing antiprotons and positrons. The photon spectrum dNγf / dEγ, with Eγ the photon energy, is expected to be proportional to ∫l.o.s. dl ρ2 (r) for annihilations and ∫l.o.s. dl ρ (r) for decays; as usual, ρ(r) is the DM density within the galaxy and the integrals are performed over the line of sight l. The dependence of ρ(r) on the above fluxes leads to a dependence of the signal on the inner distribution of DM in galaxies, modulo the fraction between the size of the dark halo and that of the telescope beam both projected on the plane of the sky (for details including the application to the Galactic Center, see Gammaldi 2016). As consequence of that, indirect searches require an accurate knowledge of the halo density profiles and, in this perspective, one should also consider cored dark matter halo distributions, in performing the analysis on the γ flux. Here, we do not further enter in this (important) issue (see, e.g., Gammaldi 2016).