4. CONSTRAINTS FROM THE EDGE OF THE OBSERVABLE UNIVERSE

Now that we have covered the basic astrophysics and the theoretical aspects of reionization, we can gain insight on cosmic reionization through some key observations. There are various independent probes of reionization, either measuring the ionization and thermal state of the IGM or the properties of galaxies forming during the EoR. The vast majority of these observations are difficult with the photons streaming across the observable universe to Earth, requiring long exposure times and/or large telescopes. Here we cover the basic physics behind each method and the latest constraints.

4.1. QSO Spectra

Light from distant QSOs can be used as flashlights to probe the intervening IGM. Neutral gas clouds at some redshift z_abs will strongly absorb light at the Lyman-α wavelength λ_α = 1216 Å in its rest frame that is then redshifted to a wavelength λ_α(1 + z_abs) in observations. The schematic and accompanying spectrum in Figure 7 depicts this technique of quasar absorption spectra mapping out the IGM. It shows that many gas clouds at varying redshifts between the QSO and us has blocked out much of the radiation at wavelengths shorter than λ_α.

Figure 7. Light from distant quasars, powered by supermassive black holes, can probe the ionization and thermal state intergalactic medium. Overdense clumps of intergalactic gas absorb some fraction of light from the intrinsic spectrum (bottom) when the photons ionize any neutral hydrogen. Only lines in the Lyman series, down to the Lyman limit (912 Å), with Lyα (1215 Å) and Lyβ (1026 Å) being the strongest. Absorption lines from clouds at various redshifts create a Lyα forest. When these lines becomes numerous enough, it creates a Gunn-Peterson trough that is indicative of an elevated neutral hydrogen fraction and the end of the Epoch of Reionization.

There have been dozens of z ≥ 6 QSO absorption spectra that have GP troughs [50], which are increasingly opaque with redshift. This is a strong constraint that cosmic reionization is complete by z ∼ 6. The IGM near QSOs are also exposed to a strong radiation field and should be more ionized than the typical IGM. This is known as the proximity effect, resulting in weaker absorption between the Lyα emission line and GP trough. The sizes of these ionized regions are on the order of tens of Mpc at z ∼ 6 (e.g. [51]). Similar to this type of analysis, absorption from a partially ionized IGM in the proximity zone will produce a damping Lyα wing that occurs when the neutral column density N_HI ≳ 10²⁰ cm⁻². The spectrum of one of the most distant QSOs at z = 7.08 constrains the ionized fraction to be x_e ≃ 0.60 at this redshift [52]. On the opposite end, there are still some neutral islands with sizes up to 160 Mpc at z = 5.5−6 [53], but they quickly erode as the increasing UV background ionizes them [50], showing that cosmic reionization is an inhomogeneous process.

4.2. The Lyα forest

The Lyα forest denotes the myriad of Lyα narrow absorption lines coming from clouds in the IGM between the quasar and us. For a cloud existing at a redshift z, they will create an absorption line at wavelength 1215(1 + z)Å. They become more abundant with increasing redshift [54] and probe clouds with column densities log(N_HI / cm⁻²) = 12−16. These lines become so abundant that they start to block out all of the background light, transforming into a GP trough at z ∼ 6. The example spectrum in Figure 7 shows a dense Lyα forest, transmitting very little light at wavelengths between Lyα and Lyβ (1026 Å). This particular spectrum transmits more light at shorter wavelengths, or equivalently, lower redshifts, suggesting that this line of sight is becoming more ionized with decreasing redshift. One constraint on the ionized fraction is the ’dark fraction’ of QSO spectra in the Lyα forest that originate from either neutral patches or residual neutral hydrogen in ionized regions [55]. Taken at z = 5.9, the dark fraction in the Lyα forest results in an lower limit of x_e > 0.94 [56].

Because Lyα forest clouds contain such small column densities, they are prone to ionization and heating from the ultraviolet background (UVB) produced by galaxies and quasars, and thus are excellent thermometers of the post-reionization universe. The UVB can be quantified by the hydrogen ionization rate

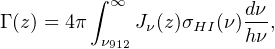(9)

that comes from the sum of ionizing photons that interact with a neutral hydrogen atom. Here σ_HI is the photoionization cross-section, J_ν is the specific intensity, and ν₉₁₂ = 3.28 × 10¹⁵ Hz is the frequency of the Lyman limit. The ionization rate can be derived from the Lyα forest lines, provided its temperature and optical depth to Lyα photons. The temperature can be calculated from Lyα forest line widths, which are affected by the Doppler effect of thermal motions of neutral hydrogen in the clouds and the thermal smoothing of the absorber over the time it has been exposed to the UVB. The optical depth can be calculated in photoionization equilibrium [57]. Data from the Sloan Digital Sky Survey (SDSS; [58]) has shown that the ionization rate is relatively constant between z = 2−5 and sharply increasing with time between z = 5−6 [59]. The ratio of ionizing to non-ionizing radiation increases by a factor of ∼ 3 going from z = 3 to z = 5, suggesting that galaxies are more efficient producers of ionizing photons at earlier times. Lastly, the sharp evolution in Γ at z > 5 could be caused by either an increase in ionizing emissivity from galaxies and black holes or the opacity of the IGM. The latter decreases after EoR as dense neutral clouds are photo-evaporated by the UVB, increasing the mean-free path of ionizing photons.

The thermal history of the IGM, probed by the Lyα forest also places constraints on the ionizing source spectra. After the cloud has been heated by some radiation source, it actually never reaches thermal equilibrium. We can consider a thermal model with the UVB as a heating source and adiabatic expansion as the coolant. Several groups have found that the typical IGM temperature is ∼ 10⁴ K at z = 5 (e.g. [60, 59]). The low-density IGM has a long cooling timescale and, thus, has a thermal memory of reionization. The exact thermal evolution depends on the timing of the initial photoheating, giving the time available to cool to ∼ 10⁴ K at z = 5 and the spectral hardness of ionizing sources [61, 62]. At later times, the double ionization of helium increases the mean IGM temperature to 3 × 10⁴ K at z = 2 (e.g. [63]).

4.3. Cosmic microwave background

While QSO absorption spectra probe the end of cosmic reionization, the CMB photons travel from the surface of last scattering to Earth and may scatter off free electrons, which is depicted schematically in Figure 8. Thomson scattering polarizes the CMB at large angular scales, resulting in a Thomson scattering optical depth τ_es that is directly related to the column density of free electrons. This measure is an integrated one and tells us little about the reionization history and only about the approximate timing of reionization. A fully ionized IGM between z = 0 and z = 6 results in τ_es = 0.039, and the remaining portion (z > 6) of the integral depends on the reionization history _e(z). The most recent Planck 2018 [13] measurement of τ_es = 0.0561 ± 0.0071, corresponding to a reionization redshift z_re = 7.82 ± 0.71 when the universe was half ionized (_e = 0.5).

Figure 8. Photons from the CMB can be scattered by free electrons, called Thomson scattering, as they propagate to detectors on Earth. Only the total amount of Thomson scattering can be measured from the CMB, which is related to the timing of cosmic reionization.

4.4. Neutral hydrogen (21 cm) absorption and emission

Figure 9. Next generation 21-cm radio telescopes that will directly explore the Epoch of Reionization.

Perhaps the most direct measure of cosmic reionization comes from neutral hydrogen emission of the hyperfine splitting of the ground state, the 21-cm transition (ν = 1420.4 MHz; E₂₁ = 5.87 × 10⁻⁶ eV). The hydrogen atom has a slightly lower energy when the spins of its proton and electron are anti-parallel than when they are parallel. The first detection of extraterrestrial 21-cm emission from neutral hydrogen happened in 1951 [64, 65], and it was not until four decades later that it was realized that 21-cm observations could be used to probe reionization [66].

When the IGM is mostly neutral, the universe is glowing in this radiation, and most of it is not absorbed as it travels toward Earth. Its detection is complicated by astrophysical foreground and terrestrial sources, especially considering that the redshifted 21-cm emission is at 101.5 [(1 + z) / 14]⁻¹ MHz, squarely in the FM band. Before any stars form, the spin temperature

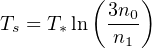(10)

measures the relative occupancy of the electron spin levels. Here T_∗ = E₂₁ / k_b = 0.0682 K, and n₀ and n₁ are the singlet and triplet hyperfine levels of the ground state. The factor of 3 comes from the ratio of statistical weights between these levels. The spin temperature tightly couples to the CMB temperature T_CMB = 2.73 (1 + z) K because the gas density is not high enough to couple with the kinetic temperature T_K that cools as a⁻² from adiabatic cosmic expansion.

Absorption or emission by neutral hydrogen changes the 21-cm (differential) brightness temperature δ T_b, which is the spin temperature relative to the background (CMB) temperature. Because the radiation is emanating from the neutral component of the IGM, it is usually multiplied by its neutral fraction (1 − _e). Positive and negative values denote emission and absorption at 21-cm. In addition to the neutral fraction of the IGM, X-ray and Lyα radiation can modify the 21-cm signal. Lyα radiation effects become dominate after z ∼ 30 as the first stars begin to form, driving a decrease in δ T_b. Then the IGM begins to be partially ionized and heated by X-ray sources, increasing δ T_b. Eventually the IGM becomes ionized by UV sources, causing the brightness temperature δ T_b to asymptote to zero as _e approaches unity. In summary, the 21-cm δ T_b signal would appear a trough that deviates from zero and should smoothly vary because it is a volume average over the Universe.

A measurement of the brightness temperature evolution would place strong constraints on the reionization history and the nature of the ionizing sources. In particular, the location of the trough in δ T_b relays information about the Lyα and X-ray emissivities of the first stars, black holes, and galaxies. Bowman et al. [67] reported on the first detection of such an absorption trough with the Experiment to Detect the Global Epoch of Reionization Signature (EDGES). It is centered at 78 MHz, corresponding to a redshift z ∼ 18, and has anomalously sharp edges and a strong amplitude. First, its timing suggests that early star formation must have been intense in low-mass (M_h ≳ 10¹⁰ M_⊙) halos [68]. Second, its shape indicates a rapid coupling of the spin temperature to the gas temperature and was not predicted by prior models [69]. Kaurov et al. [70] argue that rare and massive galaxies at z ∼ 15−20 are predominately responsible for this signal. Last, the absorption trough is consistent with a cold IGM prior to reionization. Perhaps the most mysterious aspect of the EDGES detection is its extreme depth, which suggests that the IGM is even colder than an adiabatically cooling IGM. This requires an additional cooling at very high redshifts (z = 30−100) could indicate new physics, such as interactions between baryons and dark matter [71].

There are several experiments also aiming for the same detection, which include PAPER [72], LOFAR [73], MWA [74], HERA [75], and SKA [76]. It is essential to independently confirm this groundbreaking direct detection of reionization and to obtain additional observations of this cosmic phase transition.

4.5. Sources of reionization

From the direct and indirect IGM observations just discussed, we know that cosmic reionization occurred between z = 6−15. But what sources were responsible for producing the required ionizing radiation for such a phase transition? QSOs are some of the brightest objects in the universe, but their number densities are not high enough (e.g. [77]) to significantly contribute to the UVB and the overall photon budget of reionization. The latest studies have shown that they only contribute 1–5% of the photon budget at z = 6 (e.g. [78, 79]), however see Madau & Haardt [80] for a counterpoint. This leaves starlight from galaxies to propel reionization. Two important questions about the characteristics of high-redshift galaxies are: How abundant are galaxies as a function of luminosity and redshift? How many ionizing photons escaped from these galaxies into the IGM? The first question is addressed by counting galaxies and computing a luminosity function (LF), and the second is a harder quantity to measure as a neutral IGM is opaque to ionizing photons and needs to be inferred from their UV continuum redward of Lyα.

Recent observational campaigns have provided valuable constraints on the nature of the first galaxies, their central BHs, and their role during reionization. In the rest-frame UV, the Hubble Space Telescope (HST) Ultra Deep Field [81] and Frontier Fields campaigns [82] can probe galaxies with stellar masses as small as 10⁷ M_⊙ at z ≳ 6 and as distant as z ≃ 11 [83, 84]. The LF is best described with a Schechter fit [85] as a function of luminosity,

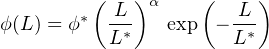(11)

that gives how many galaxies exist per comoving Mpc³ per decade of luminosity. As a function of absolute magnitude M, it reads as

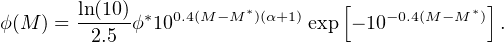(12)

The LF exponentially decays at the bright-end and is a power law at the faint-end. There are three parameters in this fit: the characteristic luminosity L^* (or magnitude M^*) that denotes the transition between power-law and exponential decay, the number density normalization φ^*, and faint-end slope α. For the purposes of reionization sources, the faint-end is the most relevant because these faint galaxies should be very numerous. However the luminosity function should flatten and decrease at very low luminosities because galaxies cannot form in small halos (see Fig. 5). The faint-end slope and the luminosity at which the LF flattens is key when computing the total number density of galaxies and their ionizing emissivity. Various groups have constrained α ≃ −2 at z ≥ 6 (e.g. [86]), and there are slight hints from the Frontier Fields that the LF flattens above a UV absolute magnitude of –14 [87, 88]. Based on this steep slope, there should be an unseen population of even fainter and more abundant galaxies that will eventually be detected by next-generation telescopes, such as JWST (James Webb Space Telescope) and 30-m class ground-based telescopes.

The ionizing emissivity (ρ_UV; in units of erg s⁻¹ Hz⁻¹ Mpc⁻³) is a key quantity in reionization calculations. Ionizing radiation is extremely difficult to observe, so we have to estimate it from the non-ionizing portion of galaxy spectra. Given a relation between total luminosity L and star formation rate (SFR), we can integrate the product of SFR and the LF over luminosity to obtain a SFR density (in units of M_⊙ yr⁻¹ Mpc⁻³). This quantity can then be converted into the ionizing emissivity ρ_UV with two factors. The first is the number of ionizing photons emitted per stellar baryon f_γ≃ 4000−13000, which depends on stellar metallicity. The second and most uncertain is the fraction f_esc of ionizing photons that escape into IGM. Finkelstein et al. [89] used Lyα forest observations to place an upper limit on the average ⟨ f_esc ⟩ < 0.13 at z = 6. However this does not prevent the average f_esc from being larger at higher redshifts [45]. Direct measurements of f_esc is impossible during EoR because the IGM optical depth in the Lyα forest only drops to unity at z ∼ 3 as these absorption systems become less abundant with time. Nevertheless, deep narrow-band galaxy spectroscopy and imaging have detected Lyman continuum emission in numerous z ∼ 3 galaxies with f_esc values ranging from an upper limit of 7%–9% for bright galaxies [90] to 10%–30% for fainter Lyα emitters [91] and 33 ± 7% for ’Lyman-continuum galaxies’ [92]. These measurements combined with theoretical calculations may be taken as a guide to the f_esc values expected from EoR galaxies.

4.6. Summary of observations

Having reviewed the primary observational constraints on cosmic reionization, there are clearly several independent measures of this grand event. The end of reionization is probed by QSO absorption spectra. The Lyα forest and GP troughs are used to constrain the residual neutral fraction (≃ 10⁻⁴ at z = 6) and remaining neutral patches. The thermal state of the Lyα forest retains some ’fossil memory’ of its initial heating during reionization and can be used to constraint the timing and heating source spectrum. Furthermore, the evolution of the UVB is determined from the Lyα forest and is steeply increasing with time at z > 5. The CMB provides both an integral measure of reionization with the universe being half-ionized at z_re = 7.82 ± 0.71. Future 21-cm experiments will be able to further constrain the reionization history and the nature of the ionizing sources. From the measurement of the steep faint-end LF slope α ≃ −2 at z ≥ 6, young star-forming galaxies are most likely the primary drivers of reionization.