


2.3. Mass and Light
There is information in the rotation curve beyond the TF relation. The shapes of rotation curves are also related to luminosity, as noted by Rubin et al. (1985) and Persic & Salucci (1991). Though I would not claim as strict a relation as implied by the ``universal rotation curve'' of Persic & Salucci, a correlation does exist and provides an additional test (Figure 2).
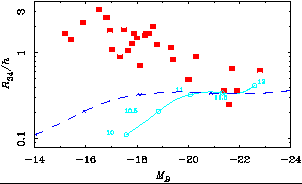
|
Figure 2. The systematic dependence of the shape of rotation curves on luminosity and disk scale length. R34 is the radius at which V(R) has reached 3/4 of the asymptotic flat velocity. A large R34 corresponds to a slowly rising rotation curve. R34 varies greatly between galaxies of the same luminosity but different surface brightness when R34 is measured in kpc. However, there is a good correlation in this diagram when R34 is normalized by the disk scale length h. Some, and perhaps most, of the scatter is attributable to observational uncertainty. Also shown are model predictions of Dalcanton et al. (1997), with numbers labeling points by the logarithm of the halo mass. The models track in the opposite sense of the data, a problem generic to SH models which have not been tuned to fit the data. |
LSB galaxies adhere to the relation between luminosity and rotation curve shape, provided that the radius is measured in units of the disk scale length (see also Verheijen, these proceedings). This implies that a good estimate of the rotation curve of any galaxy can be made from measurements of only two photometric parameters (L, h). Even though the dynamics are dominated by dark matter, we need only know the distribution of luminous matter to predict the rotation curve.
This strong coupling of mass and light (as long stressed by Sancisi) is a general problem. It always leads to fine-tuning paradoxes, with the tail wagging the dog. The dominant, spherical halo composed of non-baryonic dark matter simply should not be so intimately related to the details of the luminous disk.