2.4. CDM and NFW

I have stressed the importance of a priori predictions. There has been substantial progress in numerical investigations of the formation of halos in CDM simulations (e.g., NFW). These result in an apparently universal profile describable by two parameters, a concentration c and a scale V₂₀₀. These are tightly correlated, effectively forming a one parameter family for any given cosmology.

The data for LSB galaxies provide a good test of the these predictions (Figure 3). Because they have such large mass discrepancies, complications due to the baryonic component are minimized. The precise value of _*, adiabatic compression, feedback, etc., simply do not matter.

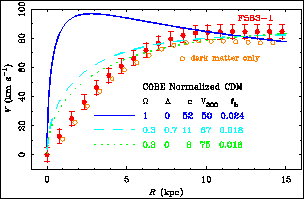
Figure 3. The rotation curve of the LSB galaxy F583-1. The solid points are the data; the open points are the remainder after the subtraction of the maximum disk component. This illustrates the large mass discrepancy typical of LSB galaxies, even at small radii. Also shown are the rotation curves due to NFW halos expected in several cosmologies. These rise too steeply at small radii, and require very low disk-to-total masses (fb) in order to match the velocity at large radii.

The predicted shape of the inner profile of the dark matter halo goes as r^- with = 1 according to NFW. Moreover, the halo parameters are specified by the cosmology. Figure 3 shows, in several cosmologies, the expected rotation curves for NFW halos chosen to be a close match to the illustrated galaxy. The predictions fail in two ways: NFW halos have rotation curves which rise too steeply, and require very low disk-to-total mass ratios.

The first failing is obvious by inspection, as first noted by Flores & Primack (1994) and Moore (1994). The data for LSB galaxies confirm and extend the conclusions of these works. There have been various attempts to wiggle out of this problem, without success (McGaugh & de Blok 1998a). Adiabatic contraction should occur at some level, but acts in the wrong direction. One might suppose instead that dwarf and LSB galaxies suffered massive baryonic blow outs following an episode of intense star formation which rearrange the dark matter in the required way (Navarro et al. 1996). There is no empirical evidence that this ever happened. Gas has not been blown away (McGaugh & de Blok 1997), nor is there any debris around LSB galaxies (Bothun et al. 1994). It now appears that the idea is unworkable even in theory (MacLow & Ferrara 1998).

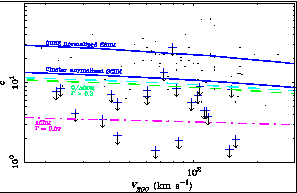
Figure 4. Predicted and measured NFW halo parameters (c, V200). These are expected to be tightly correlated in any given cosmology (lines). Different cosmologies are represented by different lines, as labeled. The data place upper limits on c by assuming stars have no mass (Pickering et al. 1997). This is unrealistic in HSB galaxies, leading to uninteresting limits (dots). The stellar mass is negligible in LSB galaxies, which place strong upper limits (crosses with arrows) on c. No plausible cosmology produces sufficiently low concentrations c to satisfy the data, even with the favorable assumption of low H0.

The problem is soluble if the amount of dark matter in the inner parts of the initial halos can be made low enough. In the context of NFW halos, this means very low c. This in turn requires a very contrived cosmology (Figure 4). Standard ( = 1) CDM produces halos which are much too concentrated. Low models (with or without a cosmological constant) fare better, but still produce halos in which c significantly exceeds the upper limits imposed by the LSB galaxy data. Using Navarros's code, the only way I have found to lower c further is to either reduce the normalization of the power spectrum well below the values inferred from COBE or clusters of galaxies, or to choose cosmological parameters (, H₀) which yield a shape parameter < 0.1. This is inconsistent with the large scale structure constraint 0.2 < < 0.3 (Peacock & Dodds 1994).

This is very bad for CDM, or at least the NFW realization thereof. Could something be wrong with the profile suggested by these simulations? Initially, there seemed to be a good consensus between different simulations. More recently, this has become rather controversial. Most workers give = 1 or > 1 (Dubinski 1994; Cole & Lacey 1996; Moore et al. 1998; Tissera & Dominguez-Tenreiro 1998; Nusser & Sheth 1998). Any 1 is inconsistent with the data.

On the other hand, Kratzsov et al. (1998) give 0.2. This is inconsistent with other simulations but consistent with the data (see Primack, these proceedings). Indeed, Kratzsov et al. (1998) constrain by fitting the data for dwarf and LSB galaxies. This constrained profile may be consistent with their simulations, but it hardly constitutes an independent test.

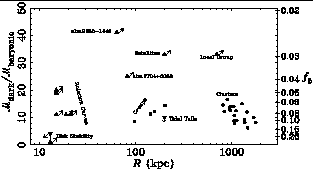
Figure 5. Measurements of and limits on the baryon fraction in various systems (McGaugh & de Blok 1998a). A single universal baryon fraction is not evident. Indeed, a number of limits are in conflict. For example, the limits for LSB galaxies refer only to the edge of the observed rotation curve (de Blok & McGaugh 1997). If we analyze them in the same way as clusters, the limits at lower left become points in the upper left portion of the diagram.

There is another problem in the baryon fraction. The general picture is of a universal baryon fraction f_b which is constant from halo to halo (giving rise, among other things, to the TF relation). A great deal of emphasis has been placed on measurements of f_b in clusters of galaxies (e.g., Evrard 1997). However, the same exercise can be done in other systems as well, with the result that there is no indication of a universal baryon fraction (Figure 5). Indeed, a number of limits are in blatant contradiction. There are various outs, too numerous to discuss here (see McGaugh & de Blok 1998a). To reconcile the cluster value of f_b 0.1 with the LSB galaxy value of f_b 0.02 suggested in Figure 3, one might suggest that not all of the baryons have been incorporated into the disk. If so, there is no reason to think the fraction which have been will be the same for all galaxies. Yet it must be. Any scatter would propagate into the TF relation, for which there is no room in the error budget.

I have long been a believer in the CDM paradigm. Yet I am forced to conclude that the accumulated evidence now weighs heavily against it. Unfortunately, the existence of dark matter is not explicitly falsifiable. Theories in which the dominant mass component is invisible have sufficient flexibility to accommodate anything.