


Galaxy formation theory fails to predict a mass distribution which yields the correct effective force law. So let us take a more empirical approach. A useful measure of the severity of the mass discrepancy is the ratio of the required gravitating mass to the total observed luminous mass. One would not expect dark matter to be aware of any particular physical scale. Is there one in the data?
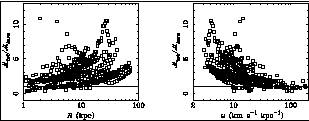
For some reason, our brains think first in terms of linear size. Galaxies are big. Is there anything special about the mass discrepancy at some large length scale? The answer is a resounding no (Figure 6a). There are galaxies for which the mass discrepancy is not apparent until quite large radii, and others (predominantly LSB galaxies) in which it appears nearly at R = 0. Size does not matter.
|
Figure 6. The mass discrepancy as a
function of (a) radius and (b)
orbital frequency ( |
There are other scales besides linear size. A plot of the mass discrepancy against orbital frequency (Figure 6b) begins to show some organization. While there is still a lot of scatter, this is a hint that there may be some interesting scale.
A scale which is truly unique to galaxies is that of low acceleration.
The centripetal acceleration which keeps stars in their orbits is typically
 1 Å s-2, only one
part in 1011 of what we
experience at the surface of the earth. The data show an enormous
regularity in terms of acceleration (Figure 7:
see also
Sanders 1990).
It matters little how
we compute the luminous mass (assuming constant
1 Å s-2, only one
part in 1011 of what we
experience at the surface of the earth. The data show an enormous
regularity in terms of acceleration (Figure 7:
see also
Sanders 1990).
It matters little how
we compute the luminous mass (assuming constant  * or maximum disk).
The reason for this is that LSB galaxies have large mass discrepancies
in either case, and also have the lowest accelerations.
* or maximum disk).
The reason for this is that LSB galaxies have large mass discrepancies
in either case, and also have the lowest accelerations.
To the best of my knowledge, there is no dark matter based prediction of this phenomenology in the literature. Attempts to impose it by fixing the surface density of dark halos fail (Sanders & Begeman 1994). It makes no sense to me that dark matter should be aware of a particular physical scale in this fashion. This is reflected in the difficulties discussed in Section 2.
The regularity of the data strongly suggest that some universal phenomenon is at work. There is one suggestion that the usual dynamics should be modified at an acceleration scale: MOND (Milgrom 1983a). Milgrom (1983b) made a series of predictions specific to LSB galaxies. I find this quite remarkable, as at that time much of the debate over LSB galaxies was about whether they existed at all, with the majority opinion being negative. Now we know they exist, and have the data to test Milgrom's predictions.
Every prediction Milgrom made about LSB galaxies in 1983 is confirmed (McGaugh & de Blok 1998b).
There are many claims to have falsified MOND. An extensive survey of the literature turns up no credible empirical evidence against Milgrom's hypothesis (McGaugh & de Blok 1998b). Indeed, there are many cases which are cited as evidence against MOND which can equally well be argued to support it (dwarf Spheroidals being one example). Are we failing to see the forest for the trees?
It remains an open question whether MOND works in all places where a mass discrepancy is inferred. But it is extremely effective at resolving the mass discrepancy in disk galaxies (Figure 7d). This is telling us something. For all practical purposes, MOND is the effective force law in disk galaxies.
Irrespective of whether MOND is correct as a theory, it does constitute an observed phenomenology. As such, it provides a very strong test of dark matter galaxy formation theories. The requirement is this: for any model, it must be possible to apply the MOND formula to the disk component and obtain the rotation curve which is actually produced by the combination of disk and halo components.
There is very little freedom to achieve this. All the many
parameters of conventional models must be encapsulated in one
tightly constrained parameter, Q. This is the ratio of
the stellar mass-to-light ratio that is required to obtain a MOND
fit to that which is `correct' in the model
(Q 
 *MOND /
*MOND /
 *DM). Since the mass-to-light
ratios indicated by MOND are already quite reasonable for stellar populations
(Sanders 1996,
de Blok & McGaugh
1998),
this is a very restrictive requirement indeed: Q
*DM). Since the mass-to-light
ratios indicated by MOND are already quite reasonable for stellar populations
(Sanders 1996,
de Blok & McGaugh
1998),
this is a very restrictive requirement indeed: Q  1
with no other adjustable parameters.
Nevertheless, this is what is required to reproduce the observed phenomenology.
1
with no other adjustable parameters.
Nevertheless, this is what is required to reproduce the observed phenomenology.
Until there is a credible explanation for the MOND phenomenology in the framework of the standard paradigm, we should be as skeptical of the existence of dark matter as we are of the need to modify Newton's Laws.
Acknowledgments
I am grateful to Erwin de Blok for our long and fruitful collaboration, and to Vera Rubin, Renzo Sancisi, Bob Sanders, and Jerry Sellwood for many animated discussions of disk dynamics.