


4.4 The Weak Distortion Regime
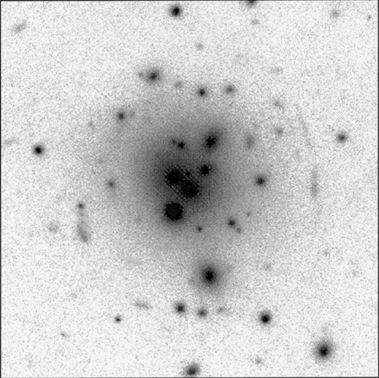
After the discovery of small distorted objects in A370 (Fort et al. 1988), Tyson, Valdes & Wenk (1990) detected ~ 50 arclets in A1689 and Fort (1992), and Kneib et al. (1994) found ~ 60 similar objects in A370. More recently, Luppino et al. (1993) found a superb case of lensing with many arclets in MS0440+0204 (Fig. 15). One of the most extensive studies of an arclet population has been done for A2218 (Pelló et al. 1992; and Fig. 14). Arclets are distant galaxies belonging to Tyson's population (1988) which are weakly lensed by the foreground cluster (Fig. 4 and 5). They could be contaminated by cluster members or by foreground galaxies, like edge-on spirals aligned along the shear axis. Since these objects are often fainter than arcs, we cannot determine their redshifts spectroscopically. Furthermore, in the weak lensing regime, the gravitational potential may only change the intrinsic ellipticity of the sources by a small amount. The effect is so small that it can only be detected from a statistical analysis of the overall background population.

|
| Figure 14. Deep CCD image of the rich cluster A2218 obtained at the Calar-Alto 3.50m telescope (Spain). Many arc(let)s surround the giant cD galaxy (top left). A second arc system is visible around another bright galaxy (bottom right) which is associated with a second concentration of mass (courtesy R. Pelló and J.-F. Leborgne). |
The theoretical analyses by Kochanek (1990) and Miralda-Escudé (1991a) show that the distribution of arclets gives the center and the velocity dispersion of the cluster. They study the local correlation between the shapes of faint objects. The basic assumptions of their analysis are: conservation of the surface brightness for the mapping of the sources onto the image plane, the valid assumptions that the amplification matrix is constant between nearby images and also that the center of the image of a source is the image of the center of the source. Since images are weakly distorted, they are identified as small ellipses of which the ellipticity and orientation are given by their first and second moments weighted by the surface brightness.
|
| Figure 15. Beautiful arcs and arclets distributed around the dense cluster MS0440+02. This is a very nice case of a circular distribution of gravitational images. (Courtesy G. Luppino) |
The analysis is summarized by the following equations:
The relationship between the shape parameters of the source
fs and the shape parameters of the image
fi is given by:
where (M-1)T is the transposed matrix.
Tyson, Valdes & Wenk first
analyzed the statistical distortion of faint galaxies
induced by a cluster (A1689). Their original idea was simply to
calculate from an arbitrary center of reference a mean distortion
parameter <T (x, y)> for all of the objects located within a given
circular window at a distance r from this reference center. The
distortion map was defined as:
where a and b are the lengths of the major and minor axes of the
image. They are related to the second order moments by the simple relation
where I, S and R
The best center of the cluster is found for the (x0,
y0) set of
values that gives the largest distortion. For a singular isothermal
sphere, the mean image distortion can be written as:
where
Note that the shear increases from the center to the critical
radius, and then decreases outside.
The Tyson et al. study concerned the region within
~ 500 h50-1 kpc from the cluster center.
They found that this cluster should have a typical velocity
dispersion of ~ 1000 km s-1, and they
gave an upper limit to the core radius of
~ 50 h50-1 kpc, in good agreement with arcs
modeling.
Kochanek (1990),
Miralda-Escudé
(1991a), and
Kneib, Mellier &
Longaretti (1992)
emphasized that
the technique has some limitations because the
redshifts and the intrinsic ellipticities of the sources are unknown.
Later, a rigorous analysis of the problem was done by
Kaiser & Squires (1993).
In principle, the
projected mass density can be recovered by analyzing the weak shear
on faint galaxies, even at distances as large as 5
h50-1 Mpc from the center.
In that case, the asymptotic behavior of the mass profile
(i.e. the slope of the potential) could be found, and possibly the
cutoff radius of the cluster.
However, measuring the weak distortion in the outermost
regions of rich clusters is a technical
challenge because the ellipticity induced by the lens on each individual
galaxy is only a few percent,
and must be measured on the faintest objects of the
field. Systematic effects associated with the
telescope (bad guiding), the atmosphere (seeing, atmospheric
diffraction), the instrument (optical distortion, bad CCD charge transfer)
induce instrumental elongations on the galaxies.
In spite of these difficulties,
Bonnet, Mellier &
Fort (1994)
attempted to measure the weak shear in the field of
Cl0024+1654. They found this cluster to be the best
candidate because it has the largest angular scale among the known
cluster lenses and is therefore a
good target to detect weak gravitational shear, even at large distances.
The cluster was observed at CFHT within ±
2 hours from zenith, in subarcsecond seeing conditions during all the
observing runs (< 0.7"). A comparison stellar field was observed
in similar conditions in order to check the instrumental distortion
all over the CCD field and the validity of the method.
A special algorithm for faint image analysis was developed and tested on
simulations (Bonnet & Mellier in preparation). The analysis
was performed
centered first on the cluster center and then on a larger
field off-centered ~ 10' from the cluster center. The most distant
region investigated is at 5 h50-1 Mpc from the
center!
The preliminary results
are impressive: the distortion is detected all around the cluster
center, and a weak shear is also measured in the off-centered field
at 3 h50-1
Mpc (Fig. 18). The coherent pattern shows an
orthoradial distribution of ellipticity of background sources
with respect to the cluster
center, as expected for a gravitational shear. From this
analysis, it is clear that Cl0024+1654 extends at least to
3h50-1 Mpc. The shear matches what is
expected from an isothermal sphere, even in the outermost region, which gives a
large mass of 4 x 1015 M
Similar studies are now in progress in various places. By using their
own faint image analysis (Kaiser & Squires in preparation),
Fahlman et al (1994)
observed the shear in the cluster MS1224 and attempted to
infer the mass profile from the Kaiser & Squires (1993) technique. They
found that the mass is about 3 times larger than the virial mass
expected from a constant M/L and suggest that dark clumps should be
present in the cluster.
Smail et al. (1994b)
analyzed with a similar
technique the cluster Cl1455+22 and Cl0016+16 but they rather suggest
that mass is well traced by light.
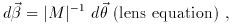
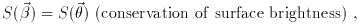
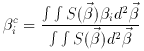
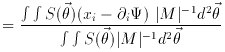
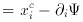
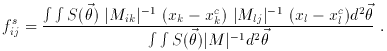
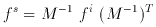
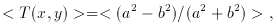
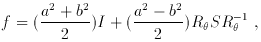
 are respectively, the identity matrix,
the diagonal matrix, and the rotation matrix. The averaged
orientation and redshifts of the image parameters are then related
to the source parameters through the shear
are respectively, the identity matrix,
the diagonal matrix, and the rotation matrix. The averaged
orientation and redshifts of the image parameters are then related
to the source parameters through the shear  and the
convergence
and the
convergence  (Kochanek 1990):
(Kochanek 1990):
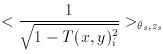
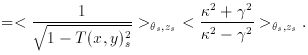
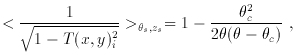
 c is
the critical radius
c is
the critical radius  c / Dd
(see section 2). However, the
distortion map is almost but not quite the dark matter map
(Kaiser & Squires 1993).
c / Dd
(see section 2). However, the
distortion map is almost but not quite the dark matter map
(Kaiser & Squires 1993).

Figure 16. Relations between the shapes of the images and
the potential. For each object we define the shape parameters
 I =
(a2 - b2) / 2ab and
I =
(a2 - b2) / 2ab and  I =
(a2 + b2) / 2ab,
I =
(a2 + b2) / 2ab,
 pot (zs) = - 2
pot (zs) = - 2 
 / (
/ ( 2 -
2 -
 2)
and
2)
and  pot (zs) = (
pot (zs) = ( 2 +
2 +  2) / (
2) / ( 2 -
2 -  2).
where a and b are the major and the minor axes of the individual
images, and
2).
where a and b are the major and the minor axes of the individual
images, and  pot (zs) and
pot (zs) and  pot (zs)
the potential parameters.
For the case of circular sources (top panel), the image is an ellipse
oriented on the main axis of magnification, and the link with the
potential is:
pot (zs)
the potential parameters.
For the case of circular sources (top panel), the image is an ellipse
oriented on the main axis of magnification, and the link with the
potential is:
 I =
I =  pot, and
pot, and  I = A
I = A  S,
where
S,
where  I is
the area of the image,
I is
the area of the image,  S of the object, and A the
magnification. For an elliptical source, the images are not oriented on
the main axes of magnification, because of the intrinsic source orientation.
The final image depends on the potential in a more complicated way, but the
principle is basically the same as for a circular source (see
Kneib et al. 1994).
S of the object, and A the
magnification. For an elliptical source, the images are not oriented on
the main axes of magnification, because of the intrinsic source orientation.
The final image depends on the potential in a more complicated way, but the
principle is basically the same as for a circular source (see
Kneib et al. 1994).
 . The shear is also
compatible with a de Vaucouleurs profile
(Bonnet, Mellier &
Fort 1994).
Unfortunately, we only observed one off-axis field.
Other distant fields around the center are needed to
confirm this result, and also to have a more precise idea on how
the shear decreases with radius. The study of the weak shear
far from cluster centers should be a real breakthrough in our knowledge
of these systems. In particular, the strong lensing regime (arcs)
combined with the radial evolution of the weak shear now gives compelling
evidence that clusters are relatively
well described by isothermal spheres with finite cores.
Flores & Primack
(1994)
discuss the physical
implications of these results for structure formation and show
that they can be severe rejection tests for theoretical models.
. The shear is also
compatible with a de Vaucouleurs profile
(Bonnet, Mellier &
Fort 1994).
Unfortunately, we only observed one off-axis field.
Other distant fields around the center are needed to
confirm this result, and also to have a more precise idea on how
the shear decreases with radius. The study of the weak shear
far from cluster centers should be a real breakthrough in our knowledge
of these systems. In particular, the strong lensing regime (arcs)
combined with the radial evolution of the weak shear now gives compelling
evidence that clusters are relatively
well described by isothermal spheres with finite cores.
Flores & Primack
(1994)
discuss the physical
implications of these results for structure formation and show
that they can be severe rejection tests for theoretical models.

Figure 18. Detection of the shear field around Cl0024+1654. The
figure is composed of two deep CCD images obtained at
CFHT which have
been rotated and co-added. The inner region of the cluster is on the
right and concerns a small field. The off-centered field is on the
left and covers a much larger field. The thick full lines indicate the
local average ellipticity computed by using about 20 of the nearest
faint distant galaxies (selected according to their colors, and with B
> 26). The orientation of the shear is given by the orientation of the
line. The pattern is
typical of a coherent gravitationally induced shear centered on the
cluster center. Note also the perturbation of the shear field in the
upper left. This effect is due to a secondary deflector locally modify
the shear field.