Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
2.3 The Problem of Formation of Structures
The above discussion is based on an idealized model of the universe,
populated by matter that is assumed to be homogeneous and isotropic;
the density  and
pressure p are taken to be spatially uniform:
and
pressure p are taken to be spatially uniform:  (t,
x) =
(t,
x) =  (t) and p (t, x) = p (t). The
real universe, of course, is quite
different and has a very inhomogeneous distribution of matter. One
possible way of characterizing such inhomogeneities is to use the
``two-point-correlation function.'' Suppose
(t) and p (t, x) = p (t). The
real universe, of course, is quite
different and has a very inhomogeneous distribution of matter. One
possible way of characterizing such inhomogeneities is to use the
``two-point-correlation function.'' Suppose 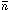 is the constant mean
number density of galaxies in space. If the galaxies are distributed
at random, the chance of finding a galaxy in a given volume
is the constant mean
number density of galaxies in space. If the galaxies are distributed
at random, the chance of finding a galaxy in a given volume  V is
simply
V is
simply 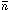
 V. If, however, the galaxies
are distributed inhomogeneously,
the chance of finding a galaxy in a volume element
V. If, however, the galaxies
are distributed inhomogeneously,
the chance of finding a galaxy in a volume element  V at a distance r
from another galaxy, picked at random, may be expressed as
V at a distance r
from another galaxy, picked at random, may be expressed as
where
This raises the question: How do we reconcile the existence of
small- scale structures - galaxies, groups, and clusters - with the
overall homogeneity of the universe? In particular, how should the
theoretical frame-work be modified to take these inhomogeneities into
account?
Two approaches are possible regarding this issue. We may try to
obtain more realistic cosmological models in which the source energy
momentum tensor of matter Tik (t, x) is
inhomogeneous and anisotropic
with an average value equal to that in a typical
Friedman-Robertson-Walker (FRW) universe. The exact spacetime metric
gik (t, x) obtained as a solution to this
problem will provide a more
realistic description of our universe. Because Einstein's equations
are nonlinear, no simple relation exists between the (large-scale)
average value of the metric <gik (t, x)> and
the average value of
Tik. Thus, this model for the universe may show
significant departures
from the FRW universe, even at large scales
(39).
This idea is
extremely difficult to put into practice, however, because of our
inability to find inhomogeneous solutions to Einstein's equations.
The alternative point of view, which enjoys considerable popularity.
is the following: Let us assume that at some very early epoch t =
ti
(say), the physical variables describing the universe had small
deviations around their mean values. The metric was gik
(t, x) =
The above picture runs into several difficulties when the details
are worked out. Of these, the following three appear to be the most
serious ones:
1. To have any predictive power in this model. we need to know the
origin and magnitude of the initial density perturbations. In the
conventional big-bang model. there is no natural seed for these
perturbations. Truly primordial perturbations, e.g. those due to
quantum gravitational effects at t
2. The second difficulty is of technical nature. We define the
``density contrast''
where (k / a) is the physical wave number and | 1 |
To every wavelength
which remains constant during expansion of the universe (since
It is usual to say that the perturbation carrying mass M enters the
Hubble radius at z = zenter or that the
perturbation with mass M was
outside the Hubble radius at z >
zenter. The discontinuity in the two
forms for Eq. 16 arises because the universe changes from the
radiation-dominated phase to the matter-dominated phase at some
teq =
4.36 x 1010 (
Notice that according to the above calculation, a galactic mass
perturbation was bigger than the Hubble radius for redshifts larger
than a moderate value of about 106. This result leads to a major
difficulty in conventional cosmology. It is usually assumed that
physical processes can act coherently only over sizes smaller than-the
Hubble radius (see e.g.
8,
17).
Thus any physical processes leading to
small density perturbations at some early epoch t =
ti could have only
operated at scales smaller than cH-1
(ti), but most of the relevant
astrophysical scales (corresponding to clusters, groups, galaxies,
etc.) were much bigger than cH-1 (t) for
reasonably early epochs!
Therefore, if we want the seed perturbations to have originated in the
very early universe, it is difficult to understand how any physical
process could have contributed to it.
(1)
3. A further major difficulty in the study of structure formation is
the following: It can be shown that the linear baryonic density
perturbations (at scales smaller than the Hubble radius) grew as
The perturbations described here, and elsewhere in this review, are
called adiabatic perturbations or curvature perturbations. They
actually change the curvature of space-time (locally, the equivalent
Newtonian potential changes by
1 The conclusion above based on
cH-1 (t)as a distance scale limiting
causal interaction is accepted by most physicists, though it is very
difficult to prove in general terms and cannot be proved by causality
arguments because cH-1 (t) and the horizon size
can be quite different
in a general FRW model (see
40,
93).
Normally, the particle horizon at
an epoch limits the range of causal communication from the past, while
the event horizon limits the range of such communication to the
future. The radiation-dominated era has a particle horizon of the
order of Hubble radius, whereas the de Sitter universe has an event
horizon of the same order. In the above argument both the horizons are
used to limit causal communication in the same sense. Moreover, for
its limited duration, the inflationary phase cannot claim even to have
an event horizon! Thus one must consider the Hubble radius in the
above argument only as a hand-waving device.
Back.
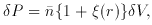
 (r) is
called the covariance function or two-point correlation
function. Detailed studies of the galaxy counts indicate that the
two-point correlation function for galaxies is
(r) is
called the covariance function or two-point correlation
function. Detailed studies of the galaxy counts indicate that the
two-point correlation function for galaxies is  (r)
(r)  (r /
5h-1 Mpc)-1.8
showing significant clustering of matter at scales r <
5h-1 Mpc
(28,
98).
On the other end, deep three-dimensional surveys indicate
evidence for filaments (100 h-1 Mpc long and
5h-1 Mpc across) and voids
(empty regions about 60 h-1 Mpc in diameter) at very
large scales
(6,
34,
47,
68,
70,
114).
The average density contrast in the universe
also shows significant variations depending on the coarse-graining
scale. It is about 105 at galactic scales and about
102 at the scale of clusters.
(r /
5h-1 Mpc)-1.8
showing significant clustering of matter at scales r <
5h-1 Mpc
(28,
98).
On the other end, deep three-dimensional surveys indicate
evidence for filaments (100 h-1 Mpc long and
5h-1 Mpc across) and voids
(empty regions about 60 h-1 Mpc in diameter) at very
large scales
(6,
34,
47,
68,
70,
114).
The average density contrast in the universe
also shows significant variations depending on the coarse-graining
scale. It is about 105 at galactic scales and about
102 at the scale of clusters.
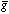 ik (t) + hik (t,
x) and the source was Tik (t, x) =
ik (t) + hik (t,
x) and the source was Tik (t, x) = 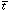 ik
(t) +
ik
(t) +  ik (t,
x), where the
quantities with an overhead bar denote the FRW values and the terms
hik and
ik (t,
x), where the
quantities with an overhead bar denote the FRW values and the terms
hik and  ik are small corrections to these mean
values. Since these
terms are small, one can linearize Einstein's equations in these
variables and study the linear growth of metric and matter
perturbations. These studies show that matter perturbations do grow
under favorable circumstances, and will reach values comparable to
their mean value in finite time
(73,
98,
122).
When this happens, the
over-dense region (effectively) decouples from the expansion of the
universe and collapses further to form a condensation. It is generally
believed that the structures in the universe arose by this process,
that is, the gravitational growth of small, primordial seed
perturbations.
ik are small corrections to these mean
values. Since these
terms are small, one can linearize Einstein's equations in these
variables and study the linear growth of metric and matter
perturbations. These studies show that matter perturbations do grow
under favorable circumstances, and will reach values comparable to
their mean value in finite time
(73,
98,
122).
When this happens, the
over-dense region (effectively) decouples from the expansion of the
universe and collapses further to form a condensation. It is generally
believed that the structures in the universe arose by this process,
that is, the gravitational growth of small, primordial seed
perturbations.
 tp, are likely to be of the order
of one [O(1)] and will be difficult to estimate. Thus, the theory
lacks predictive power.
tp, are likely to be of the order
of one [O(1)] and will be difficult to estimate. Thus, the theory
lacks predictive power.
 (t, x) and its Fourier transform
(t, x) and its Fourier transform  k (t) by the
relations
k (t) by the
relations
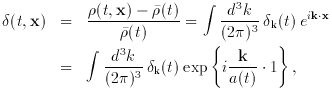
 |a (t)x| is the
proper distance. The Fourier transform separates a given inhomogeneity
into components of different characteristic sizes, which may grow at
different rates in the expanding universe. We can identify two effects
in the time evolution of
|a (t)x| is the
proper distance. The Fourier transform separates a given inhomogeneity
into components of different characteristic sizes, which may grow at
different rates in the expanding universe. We can identify two effects
in the time evolution of  (t, x): (a) the growth of the amplitude
(t, x): (a) the growth of the amplitude
 k (t) due to
gravitational instability and (b) the kinematic
``stretching'' of the proper wave lengths (2
k (t) due to
gravitational instability and (b) the kinematic
``stretching'' of the proper wave lengths (2  / k) a (t) due to the overall
expansion of the universe. Thus, a perturbation at a characteristic
physical scale
/ k) a (t) due to the overall
expansion of the universe. Thus, a perturbation at a characteristic
physical scale  0
today would correspond to a proper length of
0
today would correspond to a proper length of
 0 [a (t) /
a0]
0 [a (t) /
a0]  tn in the past, if we take a (t)
tn in the past, if we take a (t)  tn. The characteristic
expansion scale of the universe, on the other hand, is given by the
Hubble radius c H-1(t) = c(
tn. The characteristic
expansion scale of the universe, on the other hand, is given by the
Hubble radius c H-1(t) = c( / a)-1 =
cn-1t. In realistic cosmological
models, n < 1 and hence the ratio [
/ a)-1 =
cn-1t. In realistic cosmological
models, n < 1 and hence the ratio [ (t) / cH-1(t)] increases
as we go to
the earlier epochs. In other words,
(t) / cH-1(t)] increases
as we go to
the earlier epochs. In other words,  (t) would have been larger than
the Hubble radius at sufficiently high redshifts.
(t) would have been larger than
the Hubble radius at sufficiently high redshifts.
 0, we can associate the mass scale:
0, we can associate the mass scale:
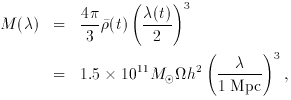

 a-3
and
a-3
and 
 a). For example
a). For example 
 1.88 Mpc corresponds to the galactic mass
of 1012 M
1.88 Mpc corresponds to the galactic mass
of 1012 M ; of course, galaxies today are much smaller, because
overdense regions have collapsed gravitationally and ceased to expand
with the universe. Thus
; of course, galaxies today are much smaller, because
overdense regions have collapsed gravitationally and ceased to expand
with the universe. Thus  is
the hypothetical size containing galactic
mass, if it had continued with the cosmic expansion. This
parametrization turns out to be extremely useful. The wavelength of
this perturbation will be bigger than the Hubble radius at all
redshifts z > zenter (M) where,
is
the hypothetical size containing galactic
mass, if it had continued with the cosmic expansion. This
parametrization turns out to be extremely useful. The wavelength of
this perturbation will be bigger than the Hubble radius at all
redshifts z > zenter (M) where,
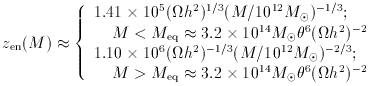
 h2)-2
h2)-2  6 s with zeq = 2.32 x
104 (
6 s with zeq = 2.32 x
104 ( h2)
h2) -4. A scale of
-4. A scale of  eq
eq  13 Mpc (
13 Mpc ( h2)-1
h2)-1  2 enters the Hubble radius at
teq, carrying the mass Meq
2 enters the Hubble radius at
teq, carrying the mass Meq
 3.19 x 1014
M
3.19 x 1014
M . Scales with
. Scales with
 <
<  eq (M <
Meq) enter the Hubble
radius before (z > zeq), when a (t)
eq (M <
Meq) enter the Hubble
radius before (z > zeq), when a (t)  t1/2, whereas
the scales
t1/2, whereas
the scales  >
>  eq
enter later (z < zeq), when a (t)
eq
enter later (z < zeq), when a (t)  t2/3.
t2/3.
 (t)
(t)
 a (t) in a
matter-dominated universe from z = zdec up to a
redshift of about (
a (t) in a
matter-dominated universe from z = zdec up to a
redshift of about ( -1 - 1) (see e.g.
98).
Since zdec
-1 - 1) (see e.g.
98).
Since zdec  1.1 x 103
1.1 x 103  -1, these
perturbations could have grown only by a factor of about
-1, these
perturbations could have grown only by a factor of about  zdec since
then. Today
zdec since
then. Today  = (
= (
 /
/  ) is of order unity at scales larger than
) is of order unity at scales larger than 
 8h-1 Mpc. Therefore, in a baryonic universe, these
perturbations must
have been at least
8h-1 Mpc. Therefore, in a baryonic universe, these
perturbations must
have been at least 
 0.8 x 10-3
0.8 x 10-3  B-1
B-1  5 x 10-3, at
decoupling if we
take into account the constraint
5 x 10-3, at
decoupling if we
take into account the constraint  B < 0.16 coming from the primordial
nucleosynthesis calculations
(130).
In the simplest models, this will
lead to a temperature anisotropy of MBR of (
B < 0.16 coming from the primordial
nucleosynthesis calculations
(130).
In the simplest models, this will
lead to a temperature anisotropy of MBR of ( T / T)
T / T)  0.3
0.3
 1.7 x 10-3
at angular scales of about 4.4'. (The angular scale of anisotropy
1.7 x 10-3
at angular scales of about 4.4'. (The angular scale of anisotropy  and the linear scale
and the linear scale  of the
perturbation producing the anisotropy
are related by
of the
perturbation producing the anisotropy
are related by 
 0.55'
0.55'  h(
h( / 1 Mpc).] No such anisotropy has been
discovered. The bounds on (
/ 1 Mpc).] No such anisotropy has been
discovered. The bounds on ( T
/ T) (less than 3 x 10-5 at 4.5'
(119)]
suggest that
T
/ T) (less than 3 x 10-5 at 4.5'
(119)]
suggest that  is less than at
least 10-4 at the time of decoupling.
This density contrast is insufficient to produce the observed
structures in a purely baryonic universe.
is less than at
least 10-4 at the time of decoupling.
This density contrast is insufficient to produce the observed
structures in a purely baryonic universe.

 k
k
 (
( phy c-1 H)
phy c-1 H)  k]. It is possible to
think of another kind of perturbation (isothermal) in which
k]. It is possible to
think of another kind of perturbation (isothermal) in which 
 = 0 but
the p = p (
= 0 but
the p = p ( ) equation changes from place to place. We do not discuss
them here because it seems unlikely that they are able to account for
structures in the universe. (For a more detailed discussion of this
and related issues, see
(7,
101,
118).]
) equation changes from place to place. We do not discuss
them here because it seems unlikely that they are able to account for
structures in the universe. (For a more detailed discussion of this
and related issues, see
(7,
101,
118).]