Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
Some of these difficulties of the standard FRW models may be
approached by modifying the dynamics of the very early universe. The
trick lies in introducing a temporary phase during which the universe
expanded exponentially as in the classical de Sitter
(35)
model. Such
an exponentially expanding phase is called inflation. The de Sitter
model described an empty universe with expansion caused by negative
stresses due to the  -term. The inflationary universe also requires a
-term. The inflationary universe also requires a
 -term; but here it arises and
is supposed to last only during the
transient stage in which the GUTs phase transition is taking place. We
consider the actual mechanisms proposed for this purpose in
Section 3.2.
Here we outline the actual model that emerges and the way it can
handle some of the awkward features of the standard model.
-term; but here it arises and
is supposed to last only during the
transient stage in which the GUTs phase transition is taking place. We
consider the actual mechanisms proposed for this purpose in
Section 3.2.
Here we outline the actual model that emerges and the way it can
handle some of the awkward features of the standard model.
Consider a model for the universe in which the universe was radiation-dominated up to, say, t = ti, but expanded exponentially in the interval ti < t < tf:
For t > tf, evolution is again
radiation-dominated [a (t)
which give an overall inflation of about A
Such an evolution, if it can be implemented dynamically, has several
attractive features. Let us first explore how this evolution helps us to
overcome some of the difficulties of the FRW models
(48,
67,
107).
Consider first the ``flatness problem,'' which concerns the unusually
small value of the curvature term (kc2 /
a2) in the early epochs.
Inflation of a (t) by a factor A decreases the value of
this term by a
factor A-2
Inflation also solves the horizon problem by bringing the entire
observed region of the last scattering surface into a causally
connected patch. The coordinate size of the region in the LSS from
which we receive signals today is
while the coordinate size of the horizon at t =
tdec will be
[We have used the relations t0 >>
tdec, A >> 1, ti
is far larger than unity for A
Inflation can also reduce the density of any stable, relic particle,
e.g. the magnetic monopoles, by a dilution factor A-3
The most attractive feature of the inflationary model is, however,
the possibility of generating the seed perturbations that can grow to
form the large-scale structures
(8,
49,
52,
111).
This can be achieved
in the following manner:
In the FRW models with a (t)
at the end of inflation. (This is, of course, much larger than the
typical Hubble radius at that epoch, cH-1
This is much smaller than the Hubble radius. This Hubble radius
remains constant throughout the inflation while
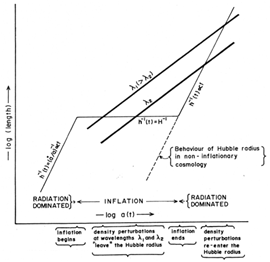
Figure 2. The figure illustrates the
growths of the length scales of
primordial fluctuations in relation to the Hubble radius during the
inflationary and Freidman phases of expansion.
The situation is summarized in Figure 2.
We see that the scales that
are astrophysically relevant today were much smaller than the Hubble
radius at the onset of inflation. (Therefore, causal processes could
have operated at these scales.) During inflation, the proper
wavelength grows, and becomes equal to the Hubble radius
cH-1 at some
time t = texit. For a mode labeled by a wave
vector k, this happens at texit (k) where,
That is, when (kc / aH) = 2
Inflationary models thus allow
What can lead to perturbations at t < texit?
Since the physical
processes taking place in this epoch are quantum mechanical by nature,
quantum fluctuations in matter fields are obvious candidates as seed
perturbations. Therefore, in principle we can now generate (and
compute) the density inhomogeneities in the universe - indeed a major
achievement of inflation.
Notice that all the above conclusions only depend on the scale
factor growing rapidly (by a factor 1030 or so) in a short time. For
example, if the energy density
where H2 (t) = [8 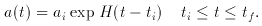
 t1/2] until
t = teq
t1/2] until
t = teq  4.36 x 1010 (
4.36 x 1010 ( h2)-2 s. Evolution becomes
matter-dominated for
teq < t < tnow =
t0. Typical values for ti,
tf, and H suggested in the literature are
h2)-2 s. Evolution becomes
matter-dominated for
teq < t < tnow =
t0. Typical values for ti,
tf, and H suggested in the literature are
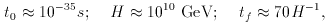
 exp N
exp N  exp (70)
exp (70)  2.5 x
1030 to the scale factor in the period ti <
t < tf. At t = ti, the
temperature of the universe is about 1014 GeV. During this
exponential
inflation, the temperature drops drastically but the matter is
expected to be reheated to the initial temperature ~ 1014 GeV
at t
2.5 x
1030 to the scale factor in the period ti <
t < tf. At t = ti, the
temperature of the universe is about 1014 GeV. During this
exponential
inflation, the temperature drops drastically but the matter is
expected to be reheated to the initial temperature ~ 1014 GeV
at t  tf. The reheating takes place when the phase
transition is over, and
the energy released in the process is passed on to the radiation
content of the universe. The situation is analogous to the reheating
that takes place when supercooled steam condenses and releases its
latent heat. Thus, inflation effectively changes the value of S
tf. The reheating takes place when the phase
transition is over, and
the energy released in the process is passed on to the radiation
content of the universe. The situation is analogous to the reheating
that takes place when supercooled steam condenses and releases its
latent heat. Thus, inflation effectively changes the value of S
 T (t) a (t) by a factor A = exp (70)
T (t) a (t) by a factor A = exp (70)  1030. Note that this
quantity S is
conserved during the noninflationary phases of the expansion.
1030. Note that this
quantity S is
conserved during the noninflationary phases of the expansion.
 10-60. Thus one can start with moderate values of
(kc2 / a2)
before inflation and bring it down to a very small value for t
10-60. Thus one can start with moderate values of
(kc2 / a2)
before inflation and bring it down to a very small value for t
 10-33
s. This solves the flatness problem, interpreted as the smallness of
(kc2 / a2). Notice that no classical
process can change a k = ± 1
universe to a k = 0 universe, since doing so involves a change in
topological properties. What inflation does is to decrease the
importance of (kc2 / a2) so much
that, for all practical purposes, we
can ignore the dynamical effect of the curvature term thus having the
same effect as setting k = 0.
10-33
s. This solves the flatness problem, interpreted as the smallness of
(kc2 / a2). Notice that no classical
process can change a k = ± 1
universe to a k = 0 universe, since doing so involves a change in
topological properties. What inflation does is to decrease the
importance of (kc2 / a2) so much
that, for all practical purposes, we
can ignore the dynamical effect of the curvature term thus having the
same effect as setting k = 0.
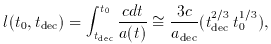
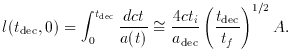
 H-1 and
adec = ai A (tdec
/ tf)1/2]. The ratio
H-1 and
adec = ai A (tdec
/ tf)1/2]. The ratio
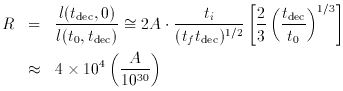
 1030. Thus, all the signals we
receive are from a causally connected domain in the last scattering
surface (LSS). Note that, in the absence of inflation, l
(tdec, 0) =
(2ctdec / adec), so that R =
2/3 (tdec / t0)1/3 <<
1. This value is amplified
by the factor 2 Ati (tf
tdec)-1/2
1030. Thus, all the signals we
receive are from a causally connected domain in the last scattering
surface (LSS). Note that, in the absence of inflation, l
(tdec, 0) =
(2ctdec / adec), so that R =
2/3 (tdec / t0)1/3 <<
1. This value is amplified
by the factor 2 Ati (tf
tdec)-1/2  107 in the course of inflation.
107 in the course of inflation.
 10-90, provided
these relics were produced before the onset of inflation. Likewise,
any discontinuities, e.g. the domain walls etc., are expanded away
from one another so that the chance of observing one by a typical
observer is made negligibly small. Further, because of the reheating
at the end of inflation, one arrives at the large entropy presently
observed in the universe. By the same token, any relic of the early
universe that survives to the present (like baryon number) must be
generated after the end of inflation.
10-90, provided
these relics were produced before the onset of inflation. Likewise,
any discontinuities, e.g. the domain walls etc., are expanded away
from one another so that the chance of observing one by a typical
observer is made negligibly small. Further, because of the reheating
at the end of inflation, one arrives at the large entropy presently
observed in the universe. By the same token, any relic of the early
universe that survives to the present (like baryon number) must be
generated after the end of inflation.
 tn (n < 1), the physical wavelengths
(which grow as
tn (n < 1), the physical wavelengths
(which grow as 
 a
a  tn) will be far
larger than the Hubble radius
[which grows as H (t)-1
tn) will be far
larger than the Hubble radius
[which grows as H (t)-1  t] in the early phases. This situation is
drastically altered in an inflationary model. During inflation,
physical wavelengths grow exponentially [
t] in the early phases. This situation is
drastically altered in an inflationary model. During inflation,
physical wavelengths grow exponentially [
 a
a  exp Ht] while the
Hubble radius remains constant. Therefore, a given length scale has
the possibility of crossing the Hubble radius twice in the
inflationary models. Consider, for example, a wavelength
exp Ht] while the
Hubble radius remains constant. Therefore, a given length scale has
the possibility of crossing the Hubble radius twice in the
inflationary models. Consider, for example, a wavelength  0 ~ 2 Mpc
today (which, according to
(15)
contains a mass of a typical galaxy
1.2 x 1012 (
0 ~ 2 Mpc
today (which, according to
(15)
contains a mass of a typical galaxy
1.2 x 1012 ( h2) M
h2) M ]. This scale would have been
]. This scale would have been
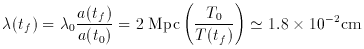
 1.4 x 10-24 cms.) But at
the beginning of inflation, its proper length would have been
1.4 x 10-24 cms.) But at
the beginning of inflation, its proper length would have been
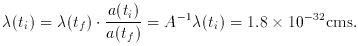
 increases
exponentially. In an interval of
increases
exponentially. In an interval of  t = t - ti
t = t - ti  18H-1,
18H-1,  will grow as
big as the Hubble radius.
will grow as
big as the Hubble radius.
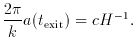
 . In the radiation-dominated era after the
inflation, the proper length grows only as t1/2
whereas the Hubble
radius grows as t; thus the Hubble radius ``catches up'' with the proper
wavelength at some t = tenter (k). For
t > tenter, this wavelength will be
completely within the Hubble radius.
. In the radiation-dominated era after the
inflation, the proper length grows only as t1/2
whereas the Hubble
radius grows as t; thus the Hubble radius ``catches up'' with the proper
wavelength at some t = tenter (k). For
t > tenter, this wavelength will be
completely within the Hubble radius.
 to be less than cH-1 at two
different epochs: an early phase, t < texit
(k) and a late phase, t >
tenter (k). Any perturbations generated by
physical processes at t < texit
can be preserved intact during texit < t <
tenter and can lead to
formation of structures at t > tenter.
to be less than cH-1 at two
different epochs: an early phase, t < texit
(k) and a late phase, t >
tenter (k). Any perturbations generated by
physical processes at t < texit
can be preserved intact during texit < t <
tenter and can lead to
formation of structures at t > tenter.
 (t) varies slowly during ti <
t < tf,
then one has near exponential expansion with
(t) varies slowly during ti <
t < tf,
then one has near exponential expansion with
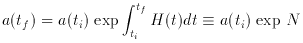
 G
G  (t) / 3c2]. This provides a
general definition of N.
(t) / 3c2]. This provides a
general definition of N.